Key Formulas

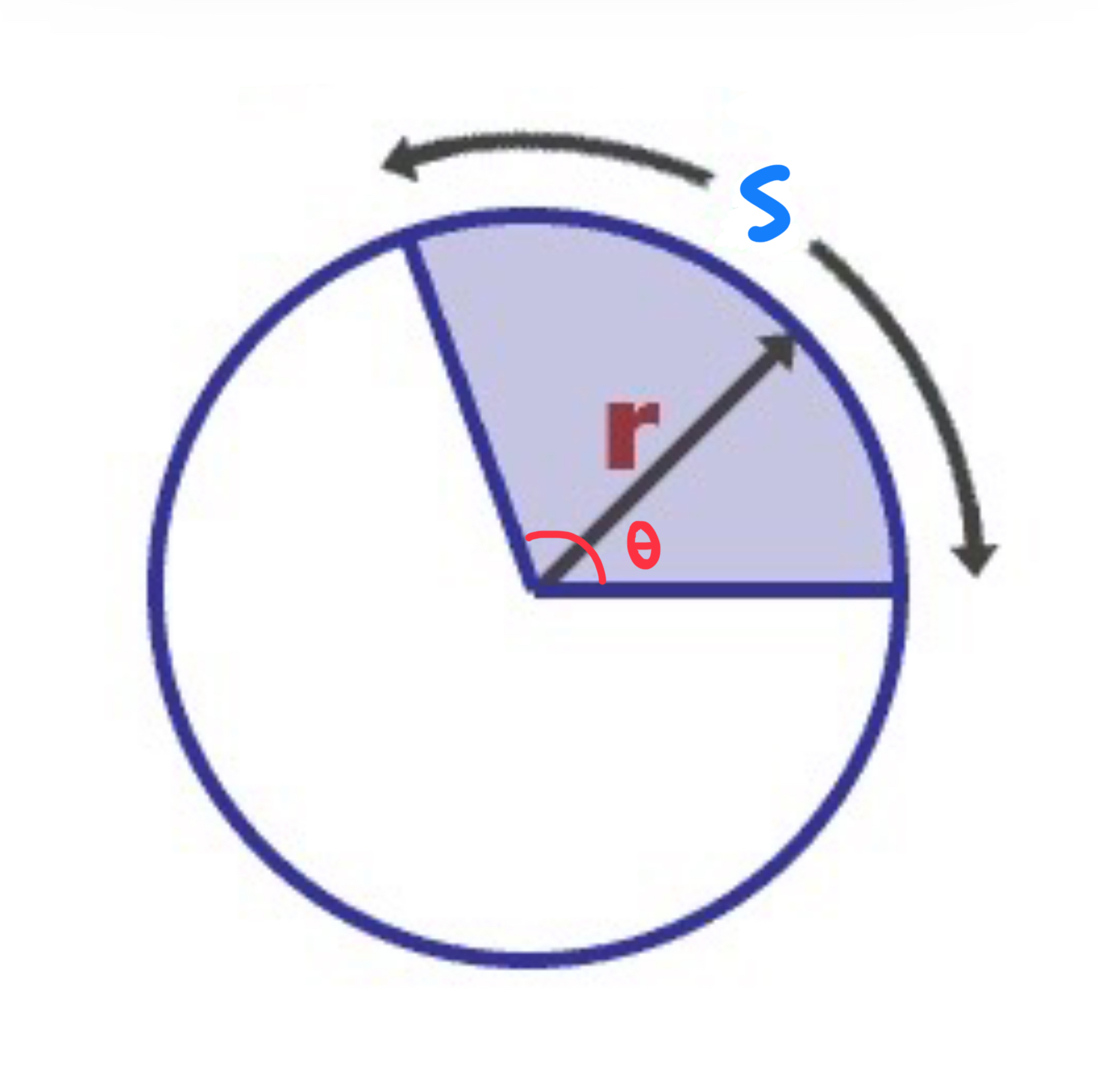
arc length

s=rθ → arc length is the distance along the edge of a circle, found by multiplying the radius by the angle in radians

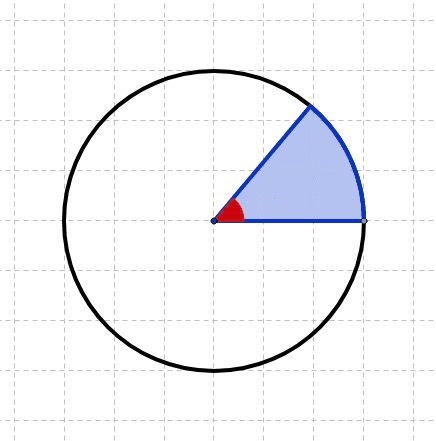
area of a sector

A=(1/2)r²θ → the area of a sector is the fraction of the circle’s area covered by the angle

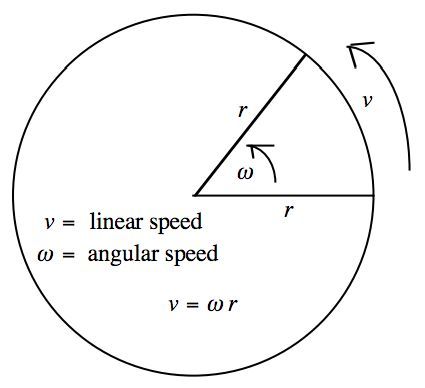
linear speed

v=s/t → linear speed is how fast a point on the circle moves along the arc, equal to arc length divided by time

angular speed

ω=θ/t → angular speed is how fast the angle changes, equal to the angle in radians divided by time

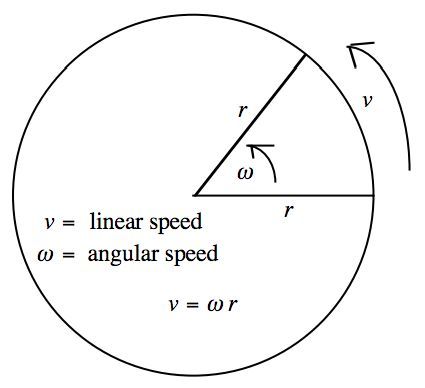
linear speed in terms of angular speed

v=rω → linear speed can also be found by multiplying the radius by the angular speed

sine

1. sinθ=opposite/hypotenuse

2. reciprocal identity: sinθ=1/cscθ

cosine

1. cosθ=adjacent/hypotenuse

2. reciprocal identity: cosθ=1/secθ

tangent

1. tanθ=opposite/adjacent

2. reciprocal identity: tanθ=1/cotθ

3. quotient identity: tanθ=sinθ/cosθ

cosecant

reciprocal of sine

1. cscθ=hypotenuse/opposite

2. reciprocal identity: cscθ=1/sinθ

secant

reciprocal of cosine

1. secθ=hypotenuse/adjacent

2. reciprocal identity: secθ=1/cosθ

cotangent

reciprocal of tangent

1. cotθ=adjacent/opposite

2. reciprocal identity: cotθ=1/tanθ

3. quotient identity: cotθ=cosθ/sinθ

pythagorean identities

1. sin²θ+cos²θ=1

2. tan²θ+1=sec²θ

3. 1+cot²θ=csc²θ

cofunction identities

1. sinθ=cos(90°-θ) → cosθ=sin(90°-θ)

2. tanθ=cot(90°-θ) → cotθ=tan(90°-θ)

3. secθ=csc(90°-θ) → cscθ=sec(90°-θ)

period

2π/B (of y=sinBx and y=cosBx) when B>0

phase shift

set Bx-C=0 to find phase shift; for y=Asin(Bx-C) and y=Acos(Bx-C)

properties of general sine and cosine functions

formulas in the picture!