Wave optics: Diffraction(2)

Continuation of the diffraction stuff froms sem 1

What is the mathematical form for the diffraction pattern from a circular aperture?

• J₁(z)= the Bessel function of the first kind of order 1

• D= the diameter of the hole

• θ= the diffraction angle

• λ= the wavelength of light.

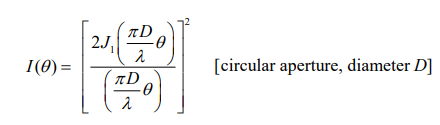
What is the mathematical form for the diffraction pattern from a 1-D slit?

• h= the width of the apeture

• θ= the diffraction angle

• λ= the wavelength of light

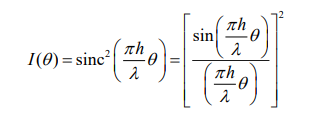
What are the similarities between diffraction by a circular aperture and a 1-D slit?

1. D and h are both simply the width of the aperture in each case.

2. So the denominators and overall-squaring are the same.

3. So we just need to compare the Bessel function to the sine.

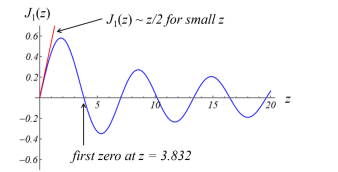
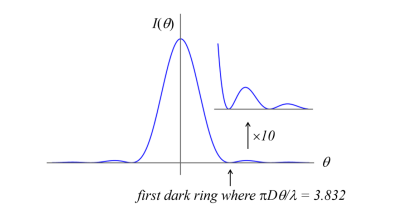
What does the plot of the Bessel function (J₁(z)) look like?

• The function is oscillatory and odd like sine

• It's not periodic and the extrema decrease with increasing z.

• For small z the ratio J₁(z)/z is finite (in this case, ½) like sinc

• The first positive zero of the function is at z = 3.832.

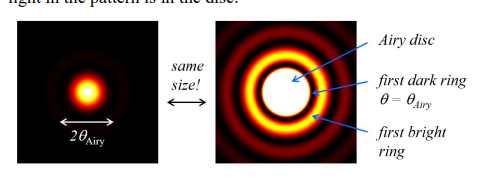
What does a diagram of the Airy pattern look like( a Fraunhofer diffraction pattern from a circular aperture)?

• It is circularly-symmetric

• It has a large central spot (the Airy disc) surrounded by faint rings.

• The Airy disc is bounded by the first zero of I(θ)

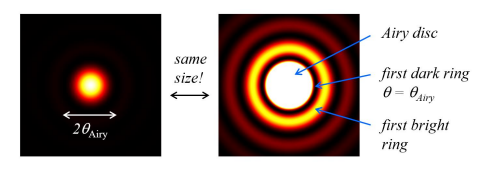
What is the Airy disc?

• The bright central spot in the Airy pattern.

• Its boundary is defined by the first zero of the intensity function I(θ), which marks the location of the first dark ring.

What is the formula that represents the first dark ring of an airy disc?

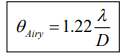
Why do lenses form finite-size Airy-pattern images of stars?

• Lenses themselves act as diffracting apertures.

• When light passes through the lens, it diffracts and forms a finite-size Airy pattern

• This results in the image of a point-like star being spread out instead of a sharp point.

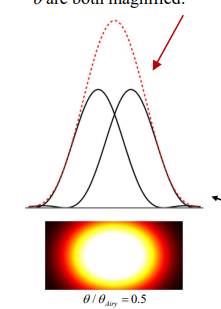
What happens when two stars, which are a small angle θ apart, are viewed through a telescope with a small aperture?

• Their Airy patterns will overlap.

• Since the Airy patterns(θ_Airy) are larger than the separation between the stars(θ), they appear as a single object and are unresolved.

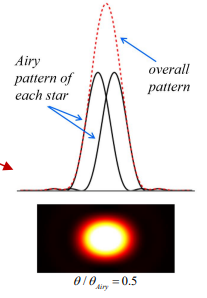
How can you resolve closely spaced stars in a telescope?

• You need a larger aperture for the telescope.

• A bigger aperture reduces the size of the Airy disc making it possible to separate the two diffraction patterns and clearly distinguish the stars.

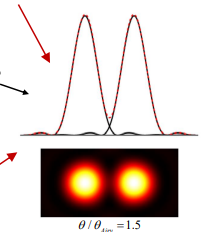
Does magnification help in resolving closely spaced stars?

No

• Both the diffraction pattern (θ_Airy) and the separation between the stars (θ) are magnified by the same factor

• Therefore the stars still appear unresolved.

What is the Rayleigh criterion definition?

Two incoherent point sources are just resolved if the centre of one's Airy disc falls on the first minimum of the other's.

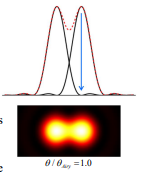
What is the condition for two sources to be resolved according to the Rayleigh criterion?

Two sources are resolved if their angular separation θ is greater than or equal to the angular radius of the Airy disc θ_Airy

What factors can make optical instruments perform worse than the Rayleigh criterion?

Factors such as:

• Optical aberrations

• Manufacturing errors

• Atmospheric effects (called "seeing" in astronomy)

What is the point spread function (PSF)?

• It describes how an optical instrument responds to light from a point source.

• If the PSF is larger than the Airy pattern, the instrument will not be able to resolve objects as sharply as the Rayleigh criterion predicts.

What does it mean for an instrument to be "diffraction-limited"?

• An instrument is diffraction-limited if its resolution is only restricted by the laws of physics,

• This happens when the instrument is free from aberrations, errors, and atmospheric effects.

What is the aperture function for Young's double-slit experiment?

The aperture function treats the two slits as a single compound aperture,

What is the formula for the intensity distribution in Young's double-slit experiment?

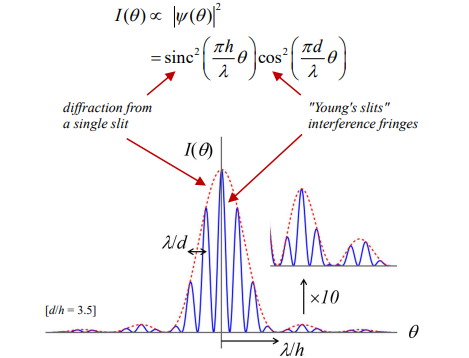
What does the diagram of the intensity distribution in Young's double-slit experiment look like?

What determines the interference fringes in Young's double-slit experiment?

• The separation d of the two slits.

• These fringes are spaced based on the path difference between light from the two slits.

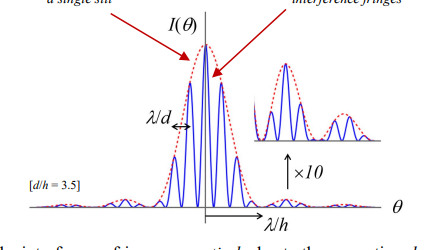
What determines the diffraction envelope in Young's double-slit experiment?

• The width h of the individual slits.

• the width hhh of the individual slits. It represents the overall spread of the light from each slit.It represents the overall spread of the light from each slit.

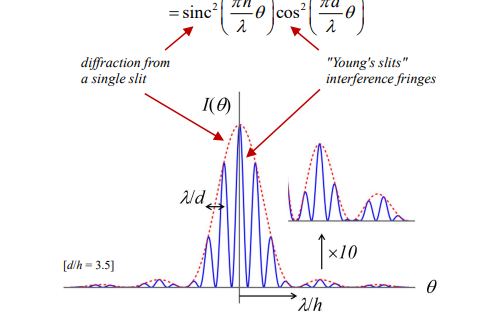
Why are the interference fringes more compact than the diffraction envelope?

The separation d between the slits must be larger than the slit width h (d>h) for distinct interference patterns to form.

How does decreasing the slit separation d affect the fringe spacing?

Decreasing the slit separation d increases the spacing between the interference fringes.

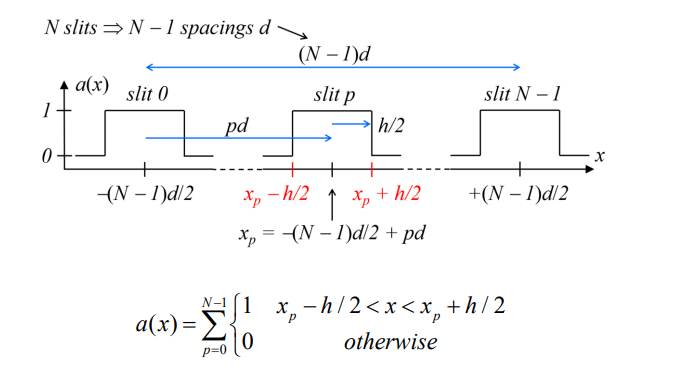
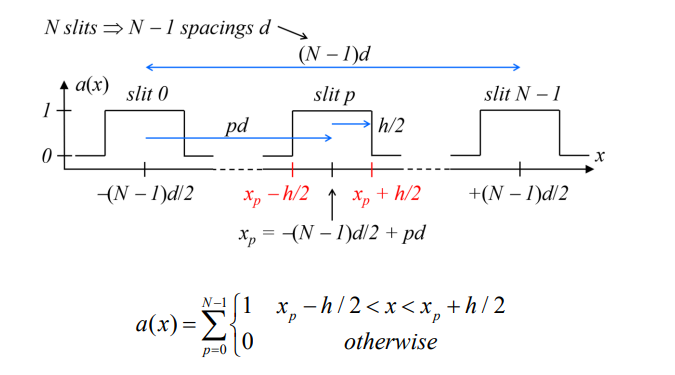
What does increasing N in a multi-slit setup result in?

Sharper interference maxima.

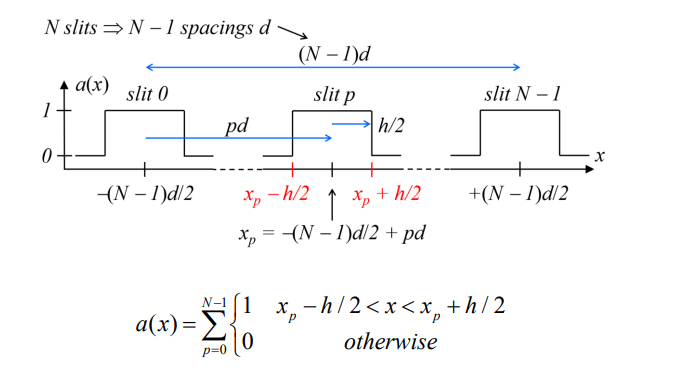
What is the width of each slit in a multi-slit experiment represented by?

h

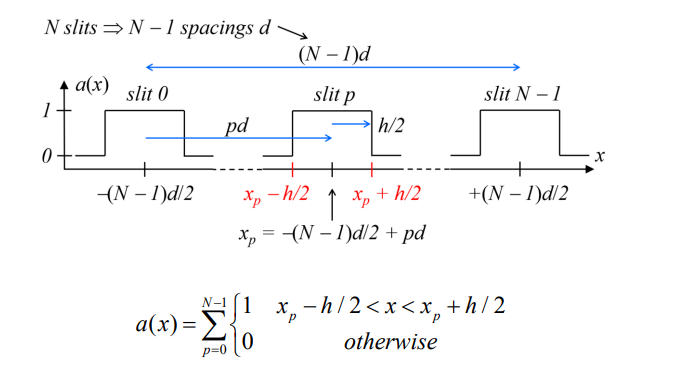
What is the center-to-center distance between adjacent slits represented by?

d

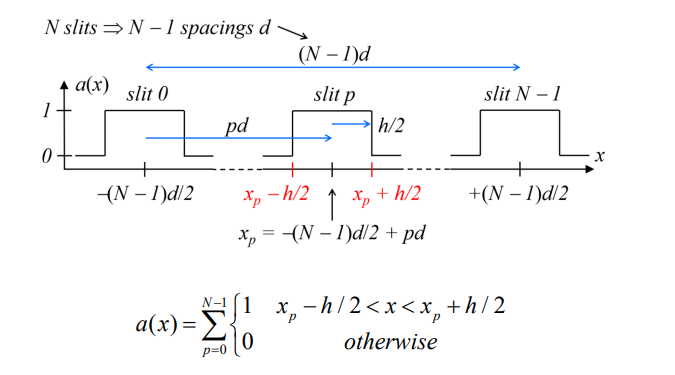
How is the position of slit p (where p=0 to N−1) defined?

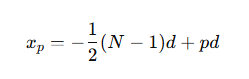
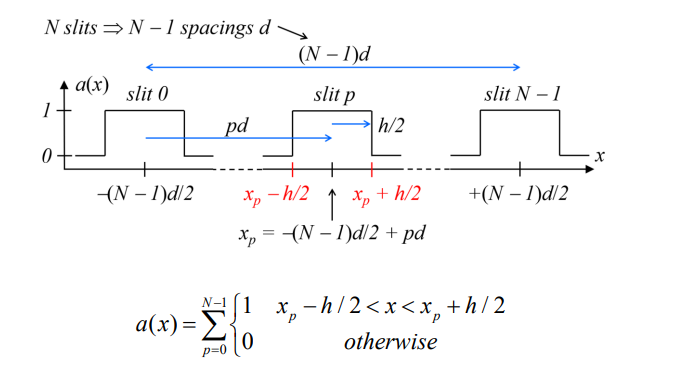
How do you define the edges of a slit at position x_p​?

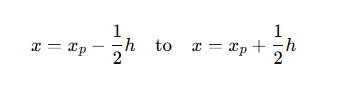
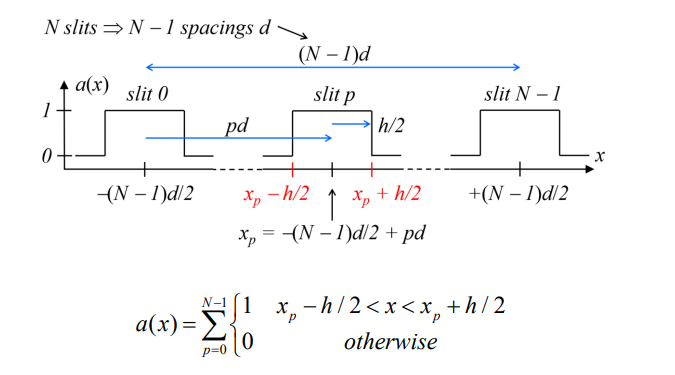
What does the compound aperture function a(x) describe?

The overall shape and distribution of the slits.

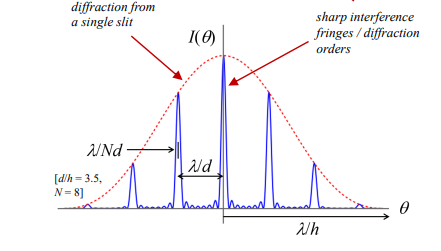
What is the equation for diffraction angles?

• d= the slit separation

• m= the diffraction order

• λ= the wavelength.

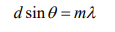
Why do diffraction gratings work for spectroscopy?

Because the diffraction angles θ of the m≠0 orders depend on wavelength λ, allowing different wavelengths to be separated.

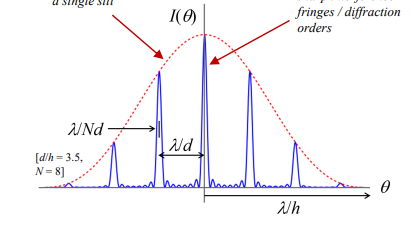
What happens to diffraction orders as the number of slits (N) increases?

The orders become much narrower, leading to higher resolution.

What is the zeroth-order (m=0) diffraction peak?

The central peak where all wavelengths constructively interfere at θ=0

How do diffraction gratings differ from many-slit apertures?

Gratings are usually reflective, while many-slit apertures are transmissive.

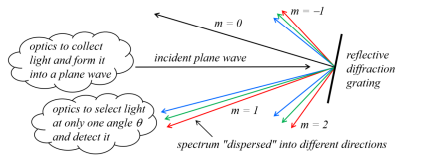
What determines the ability of a diffraction grating to resolve closely spaced spectral features?

The width of diffraction peaks in the intensity function I(θ), which depends on the number of grooves (N).

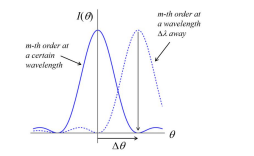
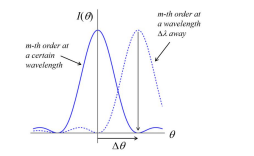
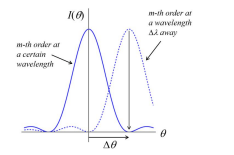
What is the half-width Δθ of a diffraction peak?

The angle range from the peak to the next zero

N= the number of grooves

d = the groove spacing

λ= the wavelength.

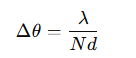
What equation describes the angle of the m-th diffraction order?

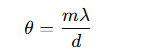
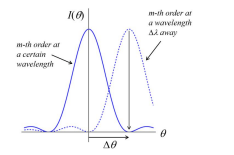
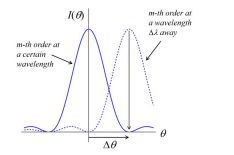
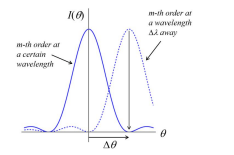
What is the Rayleigh criterion in diffraction gratings?

• Two spectral lines are just resolved when their separation is equal to Δθ

• This means the peak of one lies at the first zero of the other.

What is theformula for the resolving power R of a spectrometer?

A higher R means better spectral resolution.

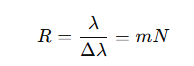
What is the minimum resolvable wavelength difference Δλ?

m= the diffraction order

N= the number of grooves.

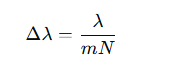
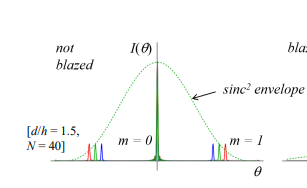
Why is the zeroth-order diffraction peak useless for spectroscopy?

Its angle θ does not depend on wavelength, making it unable to separate different wavelengths.

Why does more light end up in the zeroth order?

Because it is at the peak of the sinc² envelope, meaning it receives the most intensity.

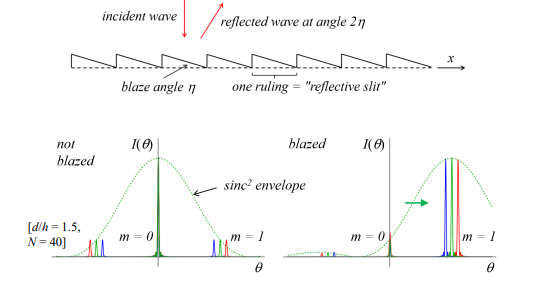
What is a "blazed" diffraction grating?

Its designed to shift the sinc² envelope peak away from the zeroth order and toward a useful diffraction order.

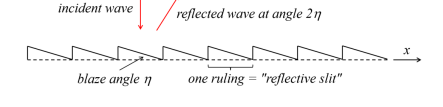
How does blazing improve diffraction efficiency?

It directs more light into a specific diffraction order (often the first order) instead of the zeroth order, enhancing wavelength separation.

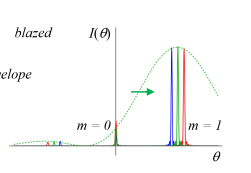
Does blazing change the location of diffraction orders?

No, the diffraction orders remain the same, but the intensity distribution shifts.