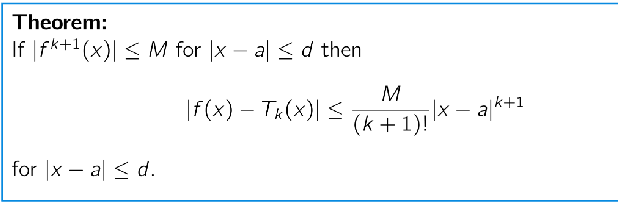Series & Sequences - Calculus

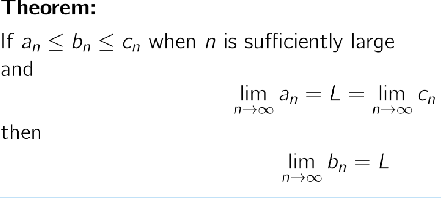
Fixed point

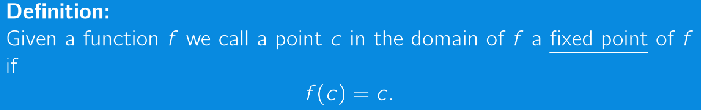
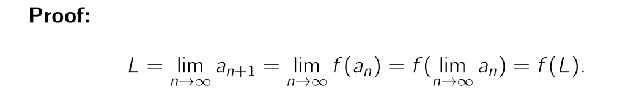
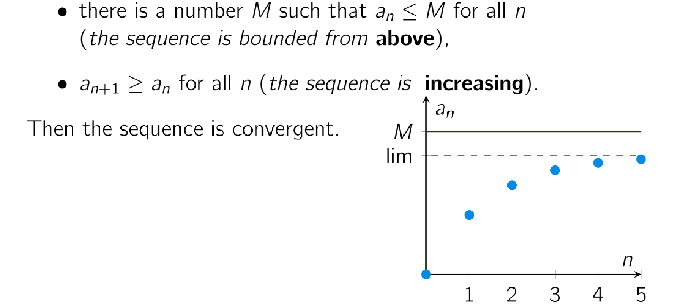
Explain monotone convergence for a sequence

If a sequence is bounded (that is a(n) <= M for all n)
AND
the sequence is increasing, a(n+1) >= a(n)

Then the sequence is convergent.
This also applies for a decreasing sequence bounded from below

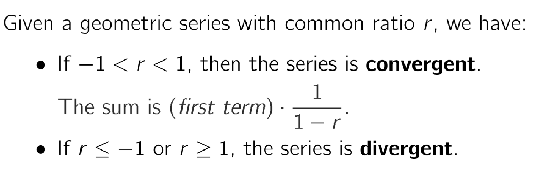
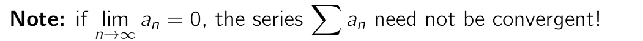
Explain why:

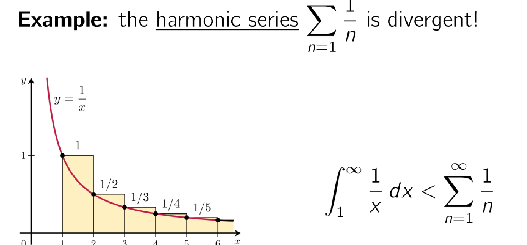
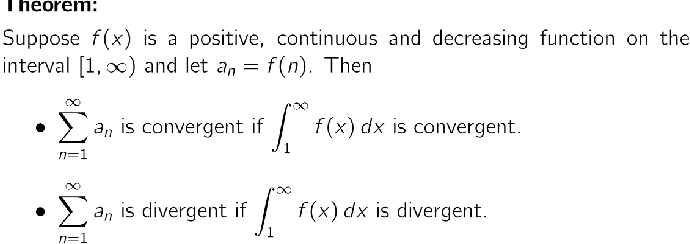
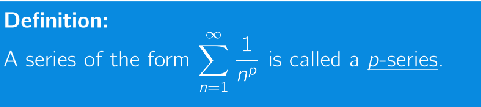
What is the behaviour of a p-series?

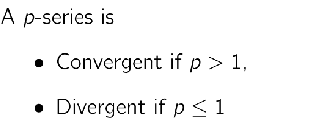
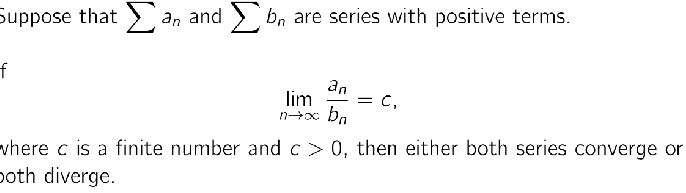
s - s(n) is basically the error margin

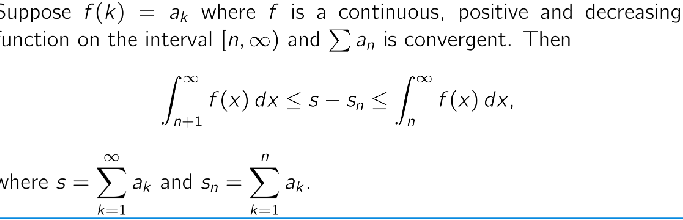
Basically we can confidently say that s is within these 2 bounds

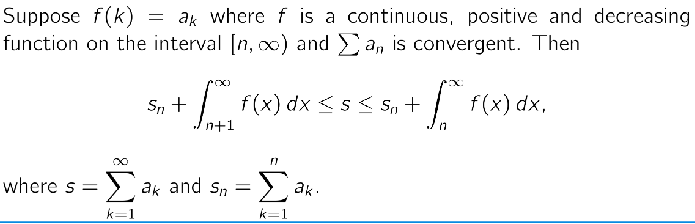
What this basically says is that the error bound is maximally as large as the next absolute value in the series

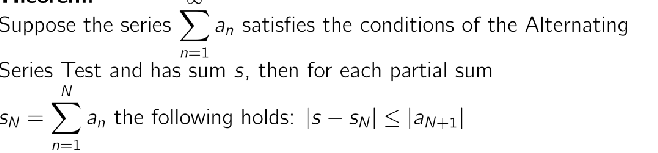
Usually, it is impossible to calculate the error for a messy series a directly.

However, if you compare it to a Geometric Series b, you can easily calculate the error for b using a simple formula.

This theorem allows you to say: "I don't know the exact error of my messy series, but I know for a fact it is smaller than 0.001 because the geometric series error is 0.001."

If every single term in list A is smaller than the matching term in list B (0 < a < b), and you know the total sum of B is finite, then the total sum of A must also be finite.

—> "If the total sum is smaller, then the Error (the leftover part) is also smaller."

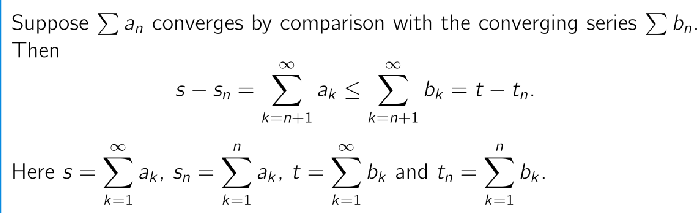
Riemann's rearrangement theorem:

Rearranging the terms of an AC series produces another AC series with the same sum.

Given a CC series and a real number r there exists a rearrangement of terms such that the sum of the rearranged series equals r.

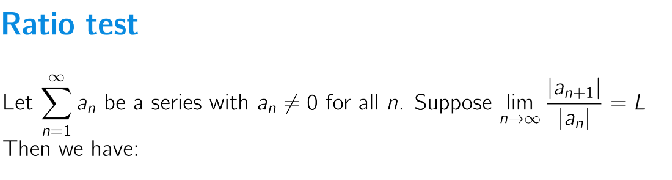
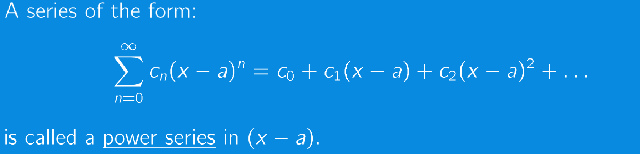
the edge points can either be convergent or divergent, we have to calculate that

How do you find the radius of convergence?

You use the Ratio Test!

How do you find the center of convergence?

Often you just read it off:

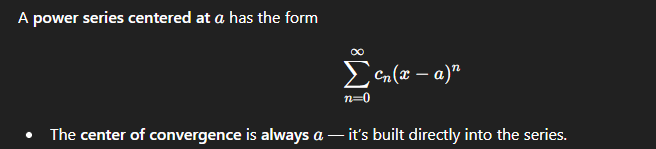
How do you find the coefficients of a function f(x)?

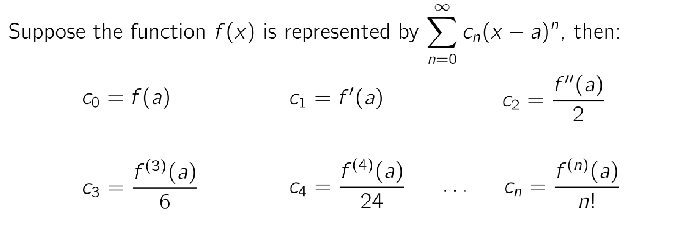
Taylor Series Definition

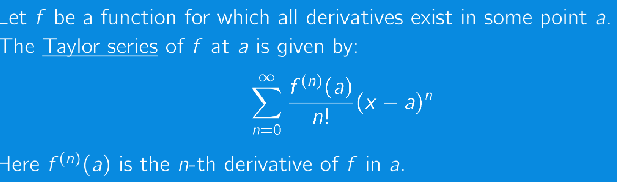
What’s the Maclaurin Series of f?

It’s basically the Taylor Series at a = 0

When is a function analytic?

To be called analytic at a, the function must equal its power series representation on an open interval containing a.
==> So not only does the Taylor Series converge to the function value at a, it also does this around a. (This radius can be variable)

Basically that the difference between the Taylor Result & the actual result is marginal

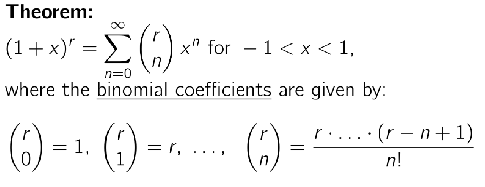
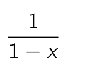
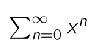
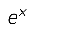
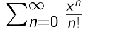
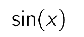
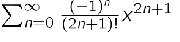
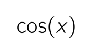
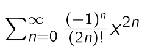
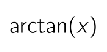
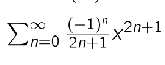
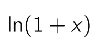
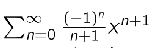
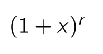
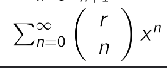
Taylor’s theorem

Taylor’s theorem essentially says that the Taylor Series are a great approximation because:
As you get closer to a, the error becomes so tiny that it is negligible compared to the polynomial terms. This guarantees that Tk(x) is the "best possible" polynomial fit for the curve at that point.

—> It is provent using L’Hopital

Taylor’s Theorem with Lagrange remainder

Basically we now know the maximal error / remainder!

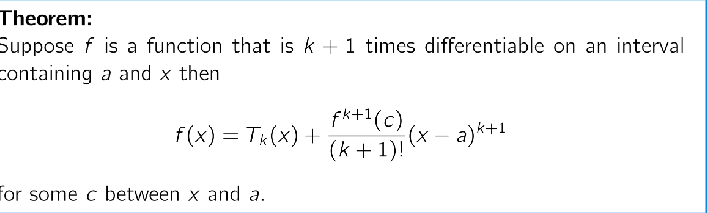
Taylor’s Inequality

"The error is less than a term built using the maximum possible derivative (M) found in the interval. —> it’s not the derivative at A but worst case scenario the largest value of that derivative between the interval (x-a) (so within d)