Sorting algorithms

OCR A-level comp sci

What are the four sorting algorithms you need to know?

• Bubble sort

• Insertion sort

• Merge sort

• Quicksort

Describe the bubble sort algorithm

• Step 1: Take a list of data to be sorted

• Step 2: Repeat step 3 (a pass) until no swaps are made:

  • Step 3: Repeat steps 4–6 for all the consecutive pairs of items in the list, starting from the first item:

    • Step 4: Compare the item at the current position to the item after it (a comparison)

    • Step 5: If the item at the current position is greater than the one next to it, swap the items within the list

    • Step 6: Go to the next item in the list

How would this list look after 1 pass of the bubble sort algorithm (sorting into ascending order)?

How would this list look after the first 2 comparisons of the bubble sort algorithm (sorting into ascending order)?

How many comparisons will bubble sort perform with the following list during the first pass of the algorithm?

6

How many swaps and how many comparisons will be made during the first pass when performing a bubble sort?

1 swap and 3 comparisons

How efficient is the algorithm below?

PROCEDURE bubble_sort(items)
    // Initialise the variables
    num_items = LEN(items)
  
    // Pass through the array of items n-1 times
    FOR pass_num = 1 TO num_items - 1
        // Perform a pass
    	FOR index = 0 TO num_items - 2  
       	    // Compare items to check if they are out of order
            IF (items[index] > items[index + 1]) THEN
            	// Swap the items
            	temp = items[index]
            	items[index] = items[index + 1]
            	items[index + 1] = temp 
            ENDIF
      	NEXT index
    NEXT pass_num
ENDPROCEDURE 

Not very efficient for a bubble sort algorithm:

• The number of passes is always n−1, even if the list is fully sorted at a much earlier point (as will often be the case).

• The number of comparisons during each pass remains the same at n−1, even though that at the end each pass, the next highest value is now in the right place

How efficient is the algorithm shown below?

PROCEDURE bubble_sort(items)

    // Initialise the variables
    num_items = LEN(items)
    swapped = True
  
    // Repeat while one or more swaps have been made
    WHILE swapped == True
        swapped = False
        // Perform a pass
    	FOR index = 0 TO num_items - 2
       	    // Compare items to check if they are out of order
            IF items[index] > items[index + 1] THEN
            	// Swap the items
            	temp = items[index]
            	items[index] = items[index + 1]
            	items[index + 1] = temp
                swapped = True
            ENDIF
	NEXT index
    ENDWHILE
ENDPROCEDURE

Alright for a bubble sort algorithm:

• If no swaps are made during a pass, the process finishes because the list is sorted

• If one or more swaps are made during a pass, there must be at least one more pass through the list

• However, the number of comparisons during each pass remains the same at n−1, even though that at the end each pass, the next highest value is now in the right place

How efficient is the algorithm shown below?

PROCEDURE bubble_sort(items)

    // Initialise the variables
    num_items = LEN(items)
    swapped = True
    pass_num = 1
  
    // Repeat while one or more swaps have been made
    WHILE swapped == True
        swapped = False
        // Perform a pass, reducing the number of comparisons each time
    	FOR index = 0 TO num_items - 1 - pass_num  
       	    // Compare items to check if they are out of order
            IF items[index] > items[index + 1] THEN
            	// Swap the items
            	temp = items[index]
            	items[index] = items[index + 1]
            	items[index + 1] = temp
                swapped = True
            ENDIF
	NEXT index
        pass_num = pass_num + 1
    ENDWHILE
ENDPROCEDURE

This is the most efficient version of the bubble sort algorithm

What is the best case scenario for a bubble sort?

• When the algorithm performs the smallest possible number of comparisons.

• This happens when the items are already in order. Then the algorithm performs only n−1 comparisons (where n is the number of items) and then stops after the first pass since no swaps were made.

What is the worst case scenario for a bubble sort?

• When the list of items you are sorting results in the greatest possible number of comparisons.

• This happens when the items are the most unordered.

• For example, they can be the original list of items in descending order and the algorithm is sorting the items into ascending order. Then the algorithm performs the maximum number of swaps per pass until all the items are ordered.

What is the time complexity of the bubble sort algorithm?

O(n²)

What is the space complexity of the bubble sort algorithm?

O(1)

How efficient is the bubble sort algorithm in terms of memory usage?

Very efficient in terms of memory requirements, as the sorting is done in the same space as the original data

An insertion sort is part way through sorting the following list of items into ascending order: 1, 23, 45, 12, 46, 3, 8

The first three items (1, 23, 45) make up the sorted sublist and the remaining items are in the unsorted sublist. The next item to insert is the number 12.

How many items will be moved when inserting this item into the correct position, including the item to insert 12?

3

Describe the insertion sort algorithm

• Step 1: Take a list of data to be sorted.

• Step 2: The sorted sublist will contain the first item and the unsorted sublist will contain all of the remaining items.

• Step 3: Repeat steps 4–9 (a pass) until the unsorted sublist is empty:

  • Step 4: Copy the first item in the unsorted sublist — this will be called the item to insert.

  • Step 5: Get the current position of the last sorted item (the item at the end of the sorted sublist).

  • Step 6: Repeat steps 7–8 while the sorted item is greater than the item to insert (a comparison) and there are still items in the sorted sublist to check:

    • Step 7: Copy the value of the sorted item up one place in the list.

    • Step 8: Get the position of the next sorted item, which is down one place from the current sorted item.

  • Step 9: The correct position has been found, which is up one place from the current position. Copy the item to insert into the correct position.

How many comparisons will insertion sort perform during the fourth pass of the algorithm and what position will the item be inserted into?

The state of the list at the beginning of the fourth pass is shown in the image. The item to insert is highlighted; it has the value 6 and is at index 4.

4 comparisons, the item is inserted at position 1.

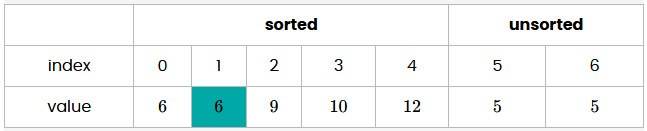
How many passes will insertion sort perform with the following list during the execution of the entire algorithm?

4

Write a subroutine that called insertion_sort that has a parameter items (passed by reference) which is a list of numbers. The subroutine should sort items into ascending order using an insertion sort.

PROCEDURE insertion_sort(items: byRef)
    
    // Initialise the variables
    num_items = LEN(items)

    // Repeat for each item in the list, starting at the second item
    FOR index = 1 TO num_items - 1
        // Get the value of the next item to insert     
        item_to_insert = items[index]

        // Get the current position of the last sorted item
        position = index - 1

        // Repeat while there are still items in the list to check
        // and the current sorted item is greater than the item to insert
        WHILE position >= 0 AND items[position] > item_to_insert
            
            // Copy the value of the sorted item up one place
            items[position + 1] = items[position]

            // Get the position of the next sorted item
            position = position - 1
        ENDWHILE

        // Copy the value of the item to insert into the correct position
        items[position + 1] = item_to_insert  
     NEXT index    
ENDPROCEDURE

How does the efficiency of insertion sort compare to that of bubble sort?

• They both pass over the list a similar number of times

• Insertion sort usually involves fewer comparisons per pass so is generally faster to execute than bubble sort (especially on large data sets)

What is the best-case scenario for an insertion sort?

• When the algorithm performs the smallest possible number of comparisons.

• For insertion sort, this happens when the items are already in order. Then the algorithm performs only one comparison during each pass since the item to insert is already in the correct position and does not need to be moved

What is the worst case scenario for an insertion sort?

• When the list of items you are sorting results in the greatest possible number of comparisons

• For insertion sort, this happens when the items are the most unordered they can be; for example, the original list of items is in descending order and the algorithm is sorting the items into ascending order

What is the time complexity of the insertion sort algorithm?

O(n²)

What is the space complexity of the insertion sort?

O(1)

How efficient is insertion sort in terms of memory usage?

The insertion sort is very efficient in terms of memory requirement, as the sorting is done in the same space as the original data.

The image shows the state of the sublists after the first merge. How will the sublists look after the second merge?

How will the sublists that need to be merged look one step before the list is sorted?

What is the best case scenario for merge sort?

• The splitting part of the algorithm repeatedly divides the list in half no matter how ordered or unordered the items are.

• The best-case scenario is when the algorithm performs the smallest possible number of comparisons during the merging stages.

What is the worst case scenario for merge sort?

• The splitting part of the algorithm repeatedly divides the list in half no matter how ordered or unordered the items are.

• When the list of items you are sorting results in the greatest possible number of comparisons - when every item needs to be compared in turn, until there is only one item left in each sublist for the final comparison.

What is the time complexity of the splitting part of the merge sort algorithm?

O(log n)

What is the time complexity of each (not all) merge in the merge sort algorithm?

• O(n)

• In the worst-case scenario, there will be n comparisons to order all n items

What is the time complexity of the merge sort algorithm?

O(n log n)

How do the best, average and worst case time complexities of merge sort compare, and why?

• The same for all three

• This is because the full split and merge process is always executed.

What is the space complexity of merge sort?

O(n)

What is a partition (in relation to quicksort)?

An unsorted section of the list

What is the pivot value in quicksort?

The value that is chosen to partition the list that is being sorted. A new value is chosen each time the list is partitioned.

Describe how the quicksort algorithm works

• Uses divide-and-conquer

• First item becomes pivot

• Compare each item to the pivot

• Make two lists, 1 with values less than the pivot and 1 with values more than the pivot

• Quick sort the new lists

• Recombine the sub-lists

What is the time complexity of quicksort?

O(n²)

What is the worst case for quicksort?

• When the pivot value is in the first or last position of the current partition as this will result in one partition with zero elements (for example, no elements to the left of the pivot value) and another partition having all the remaining elements; starting with n−1 elements.

• If this happens repeatedly (every time the list is partitioned), the next step will result in a partition with zero elements and another one with n−2 elements and so on.

What is the worst case time complexity for quicksort?

O(n²)

What is the best case for quicksort?

When each time the list is partitioned, it is divided neatly into two sections of equal size. This means log₂​n nested calls will be needed before the partition size is 1 and the base case is reached.

What is the best case time complexity for quicksort?

O(n log n)

What is the average case time complexity for quicksort?

O(n log n)

What is the space complexity of quicksort, and why?

• O(log n)

• Sorting is done in place, however

• The algorithm is recursive, which means that a call stack is used to keep copies of the data used for every partition of the list. The space complexity will therefore depend on the recursion method, and at its most efficient is O(logn).