CS 341 Midterm

Master Theorem

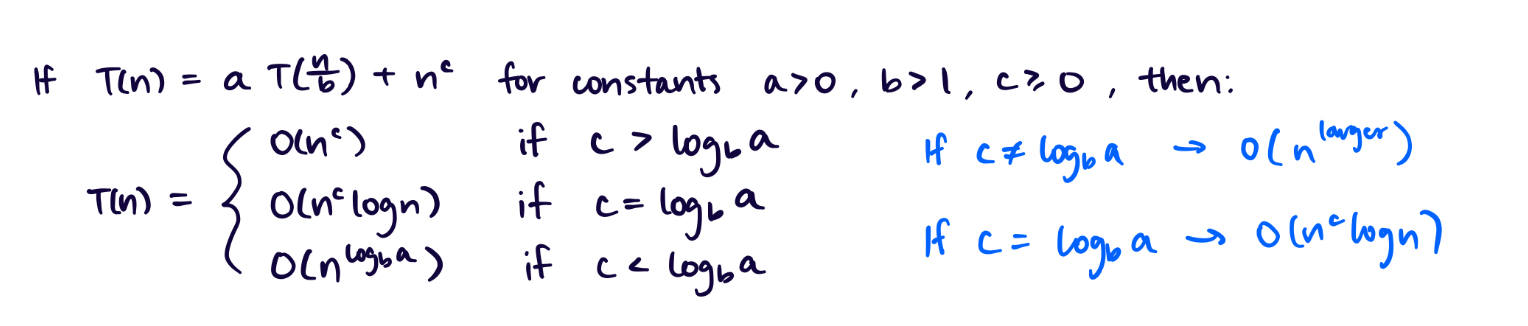
Kuratsuba’s Algorithm

• Solves multiplication of n-bit numbers with recurrence relation T(n) = 3 T(n/2) + O(n)

• subproblems: x₁y₁, x₂y₂, (x₁+x₂)(y₁+y₂)

Strassen’s Algorithm

• Solves n x n matrix multiplication with recurrence relation T(n) = 7 T(n/2) + O(n²)

BFS

• visit each neighbour first

• queue

DFS

• visit each branch first

• stack/recursion

starting time

The time at which the vertex is first encountered in the search

finishing time

the time at which all descendants of the vertex are finished being searched

Strongly Connected Component

A subset of the vertices that are maximally strongly connected

Back edge property

In an undirected graph, all non-tree edges are back edges

• tree edges refer to the edges in the DFS tree

On a somewhat related note, in a BFS tree for undirected graph, the distance of all neighbours differs by 1

3SUM

• Input: a₁, …, a_n, c

• Output: (i, j, k) such that a_i+a_j+a_k=c

• rearrange a_i+a_j+a_k=c to a_j+a_k=c-a_i

• Iterate though all values of i from 1 to n

  • At each iteration, solve the 2SUM problem with a_j+a_k

  • This is done by using a back point and front pointer to iteration over the whole list

• Time complexity O(n²)

Retrieve binary tree from pre- and in-order traversal

• Input: arrays of pre-order and in-order traversal, length n

• Output: binary tree

• Initialize a pointer that points to the start of the preorder array

• Initialize a dictionary:

  • key: inorder array element

  • value: inorder array index

• Base Case: n = 1

  • return a new node with value inorder[0]

• Recursive Case:

  • set the value of our current node to be the value at our pointer

  • increment pointer

  • set the index of our current node to be hash[root value]

  • initialize our new node with the value

  • build the left and right subtrees recursively by splitting the inorder array at the root index

Median of Medians

• Input: n/x groups of y elements

• Output: time complexity of the median selection algorithm

• Draw out the diagram and determine the number of elements in the top-left and bottom-right boxes

  • Should be of the form k = 2(n/2x)

  • Then 1-k < r < k

• This gives us P(n) = T(1-k) + O(n)

• So we get recurrence relation T(n) = T(2n/3) + P(n) + O(n)

• Resolving this recurrence relation gives us the time complexity

Counting Inversions

• Input: a₁, …, a_n

• Output: number of pairs with i < j but a_i > a_j

• Divide:

  • Cut the array in half and find the number of inversions for each half

• Conquer:

  • To count the number of “cross inversions”, we merge the 2 halves back together, because merging involves checking the # of terms in one array greater than an individual term in the other array

    • This step also implicitly sorts our array

• We return the sum of the inversions in both halves and the cross inversions

Maximum Subarray

• Input: a₁, …, a_n

• Ouput: i,j that maximizes the sum of a subarray

• Divide:

  • Split the array in half and find the maximum subarray within each

• Conquer:

  • To find the maximum crossing subarray [i,j], we need to find maximum [i, n/2] and [n/2 + 1, j]

  • By fixing i in one and j in the other, we can get the maximum crossing subarray in O(n) time for both

• Total time complexity: O(n log n)

Closest Pair

Algorithm to check if a graph is strongly connected

• Choose a random root s

• Claim: G is strongly connected iff every vertex is reachable from s, and every vertex can reach s

• Do a BFS from s and see if you can reach all vertices in one go

• Reverse all edges in G to get Gr

• Do a BFS from s and see if you can reach all vertices in one go

• If both are yes, its strongly connected

Topological Ordering

An ordering such that all the edges of the vertices point forward/downward

• If a graph is a DAG, there exists a topological ordering

Algorithm to check DAG/Topological sort

• Find all degree 0 vertices (“roots”)

  • Iterate through all vertices

  • If a vertex has in-degree 0, remove it from the graph and decrease the in-degrees of its neighbours by 1

  • repeat until there are no vertices of in-degree 0 left

    • If there are remaining vertices, its not a DAG

• Find the DFS ordering

  • Iterate through all vertices

  • If not visited yet, do DFS with that vertex as the root

  • While doing this, order the vertices by decreasing finishing time

• Find topological ordering

  • Check if the DFS ordering is a topological ordering

Algorithm to cut out SCCs

• Find DFS ordering

  • Iterate through all vertices

  • If unvisited, run DFS with the current vertex as the root

  • Order vertices in order of decreasing finishing time

• Cutting out SCCs

  • Reverse the edges of G to get G^R

  • Following the DFS ordering, perform DFS on the vertex to get its component

  • Once you have the component (all reachable vertices), cut it out

Algorithm to identify cut vertices

• We can cut out a vertex v iff the subtrees “underneath” v have no back edges that go to ancestors of v

  • This is thanks to the back edge property

• Thus, we define property early[v] as min{start[v], min{start[w] | uw is a back edge and u is a descendant of v}}

  • Measures how “far up” the neighbours of v go

• We can compute early[v] for all v in O(n+m) time

• To check whether a vertex is a cut vertex, we check if early[u_i] >= start[v] for all children u_i of v

Algorithm to identify cut edges

• Cut edges must be tree edges, not back edges

• For any parent-child edge (u,v), if it is a cut edge we are cutting out the subtree rooted at v

  • This can be cut out iff there are no back edges from descendants of v to u or any of its ancestors

• Do same thing as cut vertices, checking early[v] <= start[u]

Parentheses property

For any vertices u, v, the intervals [start(u), finish(u)] and [start(v), finish(v)] recorded during DFS are either disjoint or contained in another (u,v is an ancestor-descendant pair)