Final 303

What assumptions do we need for energy equation for 2D gas dynamics

What assumptions do we need for energy equation for 2D gas dynamics

Steady, Adiabatic, inviscid flow, no body forces

No flow is called _____ flow

quiescent

What type of nozzles can have shock diamonds?

Overexpanded

What isentropic operation on the particle must we perform for total/stagnation parameters? (6 p3 v11.0)

decelerate it to zero speed

What isentropic operation on the particle must we perform for sonic parameters? (6 p3 v11.0)

accelerate/decelerate it to sonic speed

What isentropic operation on the particle must we perform for maximum/infinite parameters? (6 p3 v11.0)

accelerate it to infinite Mach number

What type of nozzle has exhaust plumes?

underexpanded

What equation should we use for a choked nozzle?

use the St. venant equation

What equation should we use for a not-choked nozzle?

depends on your geometry

If along an isentropic streamline which parameters can be directly computed

total pressure, total temperature, and A*

Flow is ____ with a concave nozzle if A* = A min

choked

Flow is __ is diverging nozzle, if pb/p0,1 < pcrit1

choked

if pb/p0,1 > pcr,1

subsonic throughout

if pcr,2 < pb/p0,1 < pcr,1

Shock in tunnel case

if pb/p0,1 = pcr,1

Sonic speeds at the throat, subsonic everywhere else

if pb/p0,1 = pcr,2

You have normal shock at the exit of the tunnel

T or F: pcr,2 is your start and unstart condition

T (pcr,2 is your start and unstart condition)

Is all subsonic flow isentropic?

Yes (all subsonic flow is isentropic)

to properly start a tunnel, we want pb/p0,1 <= ____?

pcr,2 (46 p3 v11.0)

T or F: Sliplines move towards areas of higher pressure

F (Sliplines move towards areas of lower pressure)

For non-choked converging nozzle, what equation do we use to find the mass flow?

use mass-conservation

For a non-choked diverging nozzle, what relation do we use to find the mass flow?

use pressure relation

T or F: The higher the Mach number, the higher the pressure ratio?

F (the higher the M the lower the pressure ratio)

Shock downstream exit tunnel starts if pb/p0,1 _ pcr,2

<

Shock downstream exit tunnel unstarts if pb/p0,1 _ pcr,2 (enter a greater than or equal sign)

>

What are wave reflections?

oblique shock waves incident on a solid surface reflect from that surface in a way so that flow tangency to the surface, the no-penetration condition, is maintiained

Compression theory

use the direction of upstream flow to define deflection angle delta

What thin airfoil theory

you use freestream flow as your reference for deflection angle delta

How does exact compression/expansion theory compare to TAF?

does bad at corners but get an exact answer, only does continuous slopes well, does convex slopes well

How does exact TAF theory compare to compression/expansion?

Thin airfoil theory makes corners really easy to calculate but results are less accurate

Is this a thin airfoil?

No (Why? because it has a blunt nose!) (Groot will KILL YOU if you get this wrong)

Is this a thin airfoil?

Yes (because it has a sharp nose)

Cones beta angle will be smaller because of what 2 factors?

3D relieving effect, and flow behind the cone is non uniform

immediately behind the shock created by a cone you can assume it is ___ and ____?

steady and uniform

Is this a thin airfoil?

No (it has a blunt nose)

Shocks coming off of thin airfoils are going to be _____ and not ____

oblique and not bowed

T or F: If you have a blunt body, you end up with a bow shock somewhere in front of the stagnation point

T (all blunt bodies will create a bow shock eventually)

Which assumptions do we use for prandtl-meyer?

everything except isentropic and reversible

What laws do we need to derive the prandtl-meyer relation?

all 3

Compression shocks are ___

irreversible

expansion shocks are ____

non-existent (destroys entropy, violates 2nd law of thermo)

Direction of vorticity

Determined by the right hand rule

T or F, the boundary layer is NOT adiabatic

T (boundary layer have some heat dissipation due to viscous effects)

The gradient of entropy points towards the ___ every time?

body (because velocity is always going to eventually become parallel to the body, the change in entropy is perpendicular to velocity)

T or F: velocity near the symmetry line is always smaller than when it is far away

true (because of viscous effects and boundary layer slowing down the flow)

T or F: moving shocks are always unsteady

T (moving shocks are by definition unsteady always)

T or F: shocks are always unsteady

F (you can have a stationary shock like for a wind tunnel)

If Prandtl-Meyer function were valid in the case of a trivial solution, it makes the most physical sense that ___?

straight streamtubes should support sonic flow

What is the definition of the camber line?

the midpoint between upper/lower surface in x-y frame

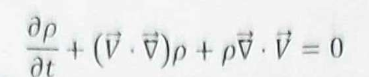
Tick the single box that indicates the fundamental law that forms the basis for the transport equation for the density. Options are Mass conservation, Newton’s 2nd law, or 1st law of thermodynamics

Mass conservation

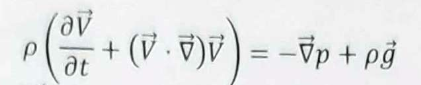
Tick the single box that indicates the fundamental law that forms the basis for the transport equation for the flow velocity. Options are Mass conservation, Newton’s 2nd law, or 1st law of thermodynamics

Newton’s 2nd law

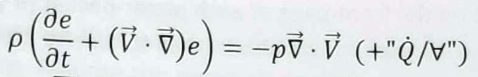
Tick the single box that indicates the fundamental law that forms the basis for the transport equation for the specific internal energy. Options are Mass conservation, Newton’s 2nd law, or 1st law of thermodynamics

1st law of thermodynamics

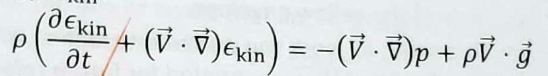
Tick the single box that indicates the fundamental law that forms the basis for the transport equation for the specific kinetic energy. Options are Mass conservation, Newton’s 2nd law, or 1st law of thermodynamics

Newton’s 2nd law

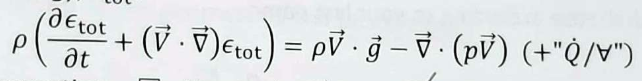
Tick the single box that indicates the fundamental law that forms the basis for the transport equation for the specific total energy. Options are Mass conservation, Newton’s 2nd law, or 1st law of thermodynamics

1st law of thermodynamics

What 4 things do we assume to use the method of characteristics in specific form

Adiabatic, Irrotational, Inviscid, and steady

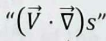
Briefly explain what the statement “(V dot nabla) s” means

entropy change in the flow-velocity direction (aka the streamline) aka (Velocity dotted with the gradient of the entropy)

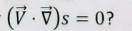
What conditions are necessary for ( V dot nabla) s = 0?

steady, adiabatic, and inviscid flow

With the change from irrevesible requirement to irrotational, only ____ and ____ are anisentropic

boundary layers and flow behind curved shocks

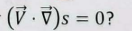
Consider the flow through a (strong) stationary shock wave. What conditions are required for (V dot nabla) s to equal 0

inviscid flow

What assumption(s) are necessary to assume vorticity to be constant along streamlines:

steady flow, barotropic flow, irrotational flow

Assume that the velocity vector V points to the left and the vorticity vector points out of the page. What is the direction of the entropy gradient delta s?

down

Crocco’s theorem tells us these flow condition(s) imply isentropic flow (options are steady, adiabatic, irrotational, or reversible flow)

steady, adiabatic, and irrotational

In which flow regime(s) do we find the maximum entropy?

G

In which flow regime(s) do we find the minimum entropy?

A, B, C, D

Tick the flow region(s) that support rotational flow

E, F, and G

What is the direction of the entropy gradient, nabla s, in the region(s) of the diagram that supports rotational flow?

perpendicular to the direction of streamlines and upward

In which direction does the vorticity vector point?

out of the page

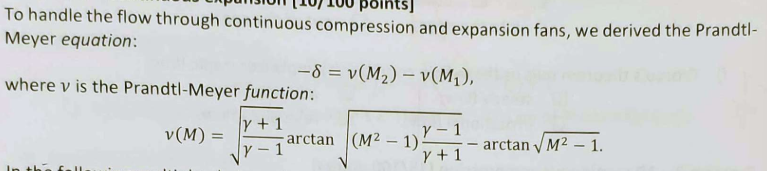
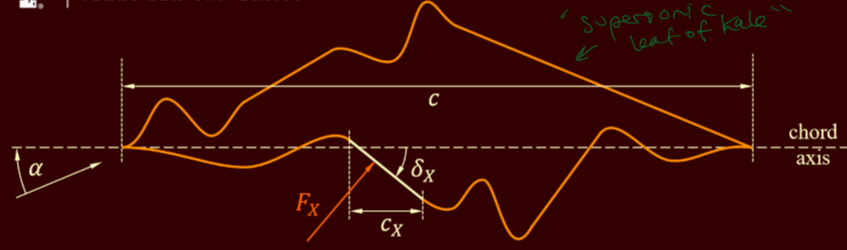
What is the delta? Options: initial mach-wave angle, terminating Mach-wave angle, flow-deflection angle with respect to an arbitrary horizontal coordinate, flow-deflection angle with respect to the flow immediately upstream of the considered compression/expansion fan

flow-deflection angle wrt flow immediately upstream of the considered compression/expansion fan

What determines the sign of delta?

whether the flow is compressed or expanded

Can we use the Prandtl-Meyer equation to solve subsonic-flow problems and why?

No (still working on the why part)

the method of characteristics, in the specific form in which we derived and applied it, is restricted to

steady, adiabatic, irrotational, inviscid flow

Pick one or more applicable answers for the method of characteristics from the following interdependent options: (2D flow, axisymmetric flow, full 3D flow)

2D flow

Pick one or more applicable answers that we can use the method of characteristics on from the following independent options: (subsonic, sonic, or supersonic flow)

supersonic

Is the method of characteristics valid for the calculation of the flow through a strong shock wave? why?

no because the method of characteristics requires isentropic flow and strong shocks are anisentropic

In the expressions for the Riemann invariants: K = nu +- delta, what is delta?

the direction of the flow with respect to an arbitrary horizontal (x) component

In our derivation of the Method of Characteristics, we approximate Mach waves as (increasingly more) piecewise-linear line segments. In which of the unknown variables does this approximation produce an error?

Node locations only, the resulting M, delta, and thermodynamic variables are exact

Using exact theory, calculate the pressure coefficient corresponding to region 5, Cp,5

?

What does it mean for a pressure coefficient to be negative

this means the flow is in an expanded state versus the freestream.

In the definition of Cp, why do we use the freestream, dynamic pressure Q infinity?

this is inherited from incompressible flow. Cp = 1 corresponds to stagnation in incompressible flow only (as Mach tends towards zero Cp tends to 1)

Next, let’s discuss the flow downstream of the trailing edge. An educated guess is that the flow downstream of the TE is aligned with the freestream direction. Based on the given direction, how should the slip line be deflected to improve our assumption for the slip line’s direction

Upwards

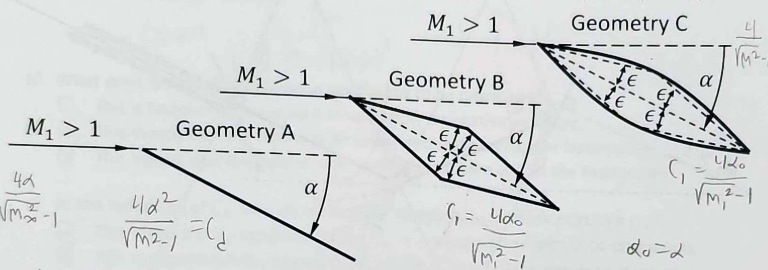
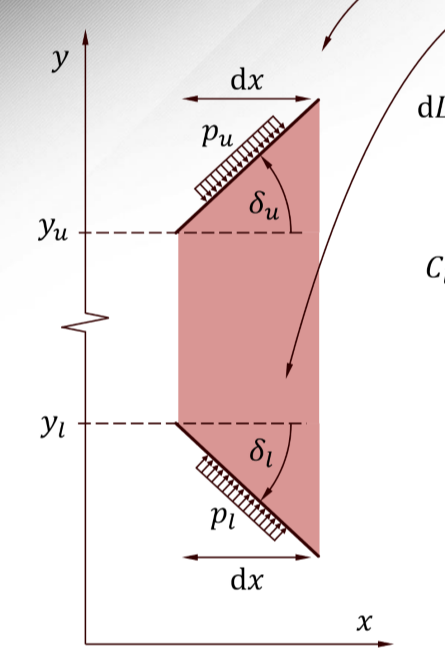
Using thin airfoil theory consider the geometries shown below and assuming M1 and angle of attack are the same for all, how do the lift coefficients of these airfoils relate? Explain

C1,A = C1,b Since the geometry can be simplified to flat plates, they share the same Cl relying only on alpha and is independent of camber

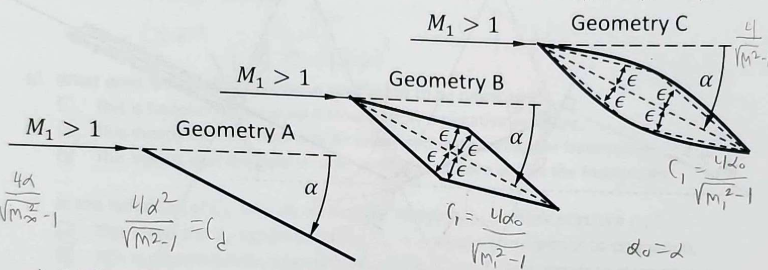
Using thin airfoil theory consider the geometries shown below and assuming M1 and angle of attack are the same for all, how do the drag coefficients of these airfoils relate?

Cd,A < Cd,b < Cd,C because drag depends on camber and thickness for complex geometry. Since all contributions are positive, B and C are greater than A

What assumptions do we need to use thin airfoil theory?

All flow deflection angles are small (imposed either by the geometry or alpha and irrespective of whether the deflections are concave or convex)

If the thin airfoil assumption is/assumptions are justified, what can we say about the angles of shock waves and expansion fans? They:

all collapse down to Mach angles, which are not necessarily close to 0 degrees.

Can we treat the airfoil below as a thin supersonic airfoil?

No (it has a blunt nose)

In the formula for the pressure coefficient corresponding to thin airfoil theory: Cp = 2delta/sqrt(M²-1). Which Mach should be used?

The freestream mach number (because the M will vary infinitesimally throughout the flow field)

The zero reference for the flow deflection angle delta:

the freestream direction, because subsequent deflections add up to the deflection with respect to the direction of the freestream

Change in entropy through Mach waves is …?

zero because Mach waves are isentropic

While increasing pb, which of the geometries will support underexpanded flow last?

A (because

while increasing pb, which of the geometries will unstart last?

A

While increasing pb, which of the geometries will support choked flow last?

C and D

while increasing pb equally slowly for each of the geometries and setting Amin equal for all geometries, which of the geometries do we expect to have drained the reservoir the most as we land at sea level?

C and D

What column of NACA 1135 can you NOT use to calculate for a pitot tube problem

2nd to last column (it doesn’t account for the anisentropic effects of a shock)