Rational function: Obtained through the division of polynomials

• Sometimes there’s an x in the numerator

• There is always an x in the denominator

• No passing through asymptotes, no right angles, no curving back on yourself

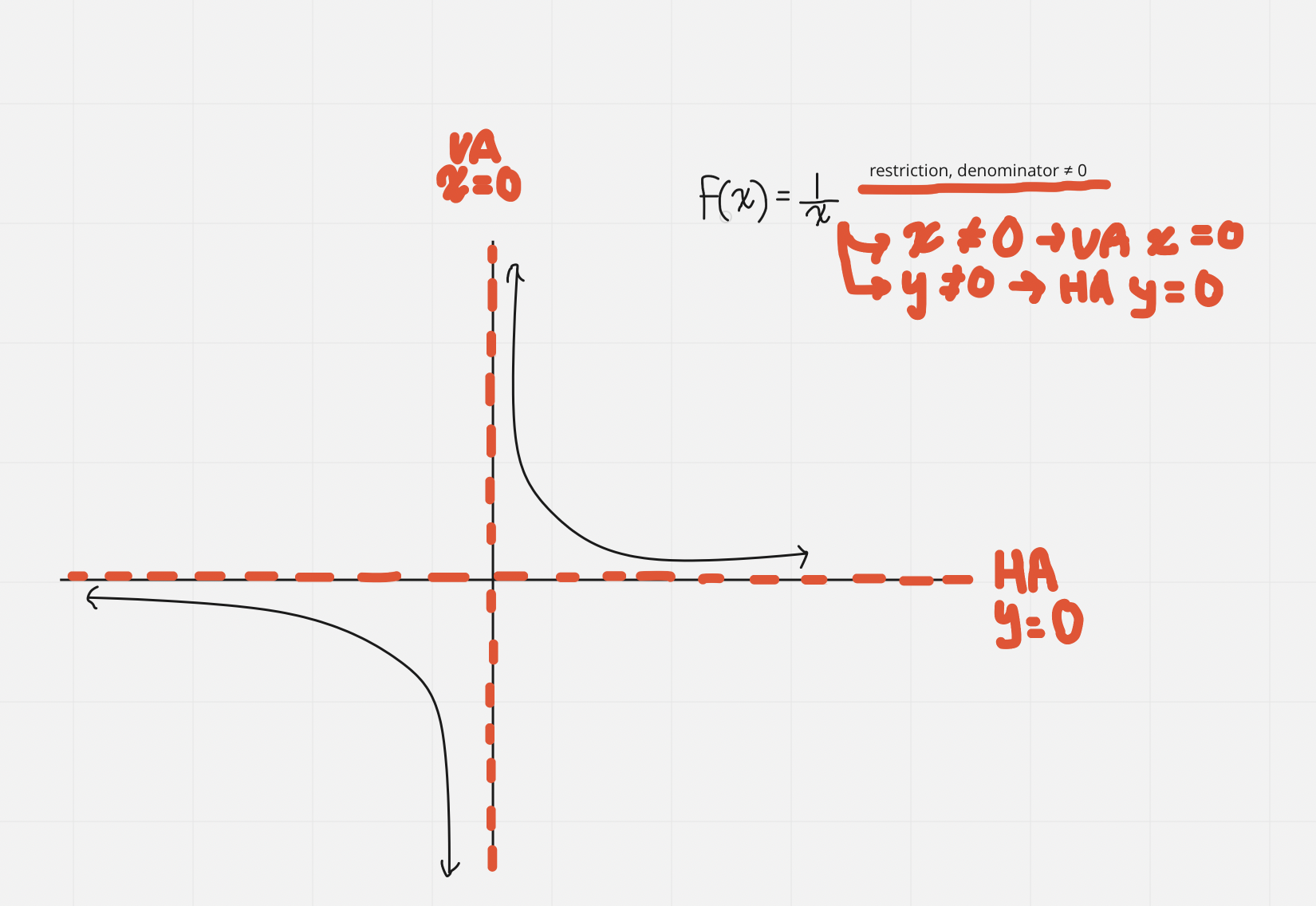
• Horizontal asymptotes are less strict than vertical asymptotes

Behaviour Near Asymptote

When graphing rational functions, it is useful to know what is happening as we approach both the vertical & horizontal asymptotes

For Vertical Asymptotes (VA):

In order to see the behaviour as we approach the vertical asymptote, we want to know what is happening to the y values as we approach the VA from both the left and right sides

For Horizontal Asymptotes (HA):

In order to know the behaviour as we approach the HA, we want to know what is happening to the y values as x→ ∞ and as y → ∞

Notation

a little + at the top of the number means to the right of, a little - to the top of the number means to the left of (think of it as a number line)

Reciprocal of a Linear Function

General formula:

• Degree of numerator is equal to the degree of the denominator

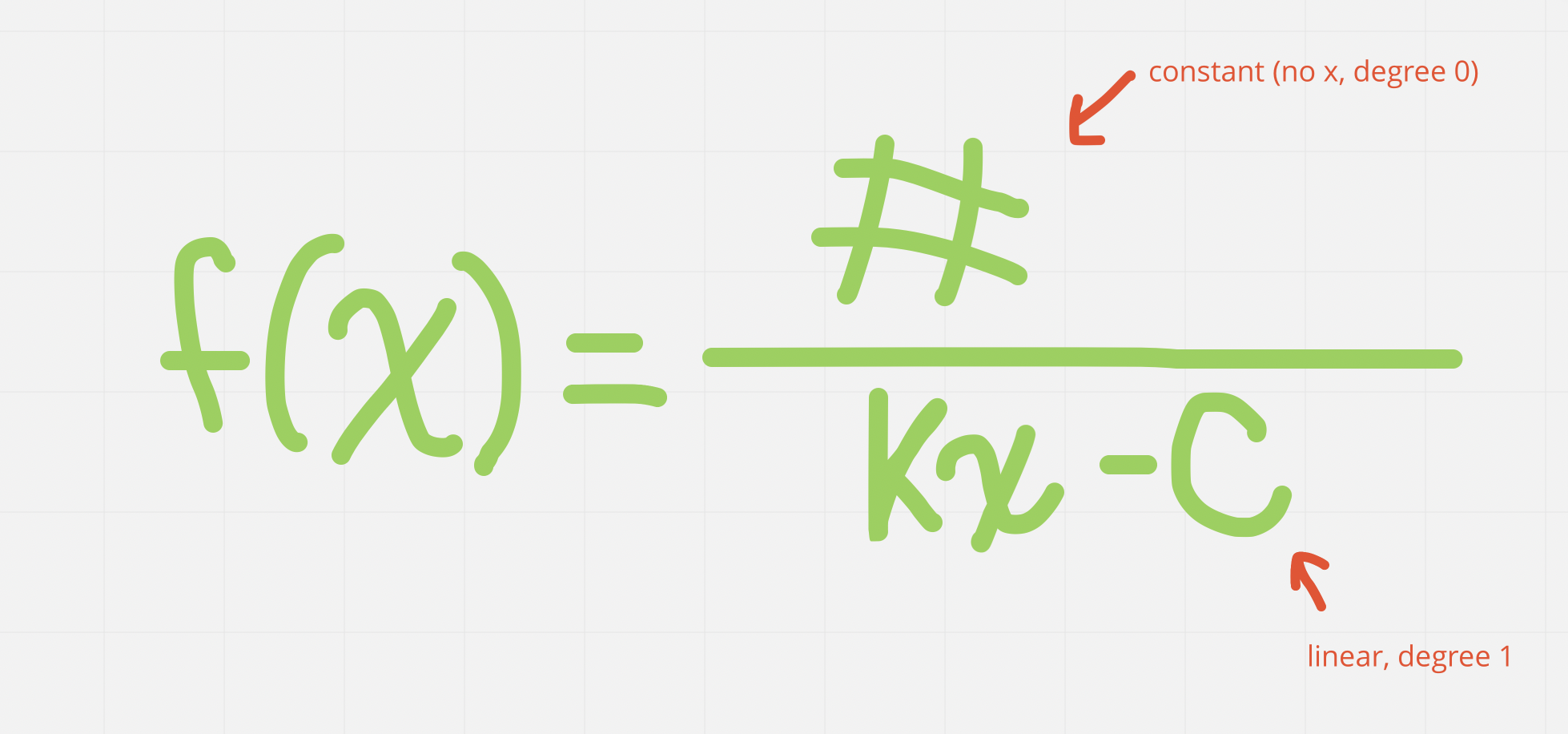
Procedure for the Reciprocal of a Linear Function

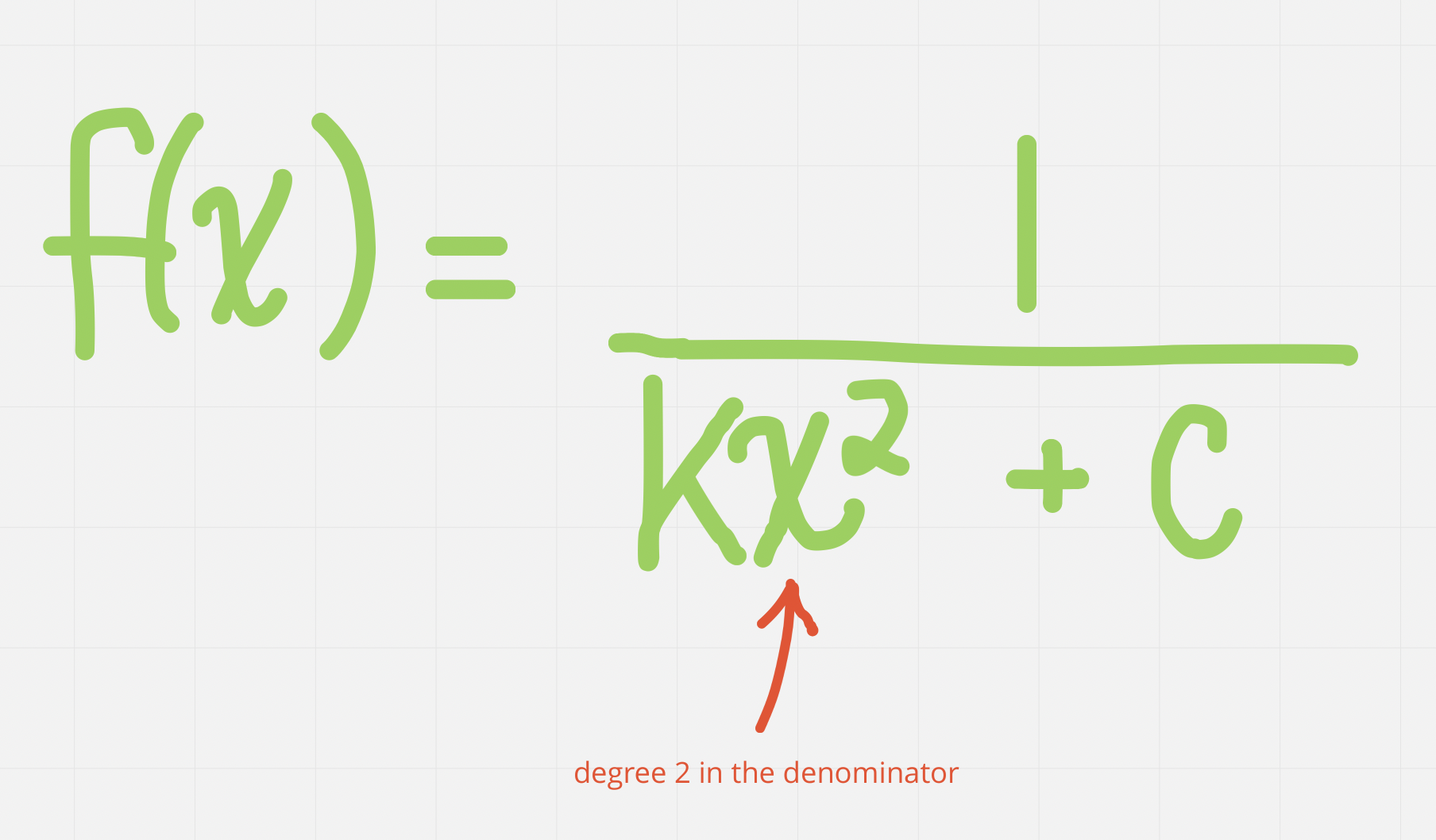
Reciprocal of a Quadratic Function

General formula:

• Degree of the denominator is greater than the degree of the numerator

A reciprocal function’s key features:

• Asymptotes, HA and VA

• Intercepts, x int and y int

• Domain and range

• End behaviour/behaviour near asymptotes

• Positive/negative intervals

• Slope, positive/negative; increasing/decreasing

Process

• Factor the denominator before operating

• You will have 2 VAs

• Same process as with reciprocals of linear functions

• There will be a vertex and the quadratic reciprocal function is almost opened up (if you think of linear reciprocal function as folded up)

Find the vertex:

Rational Functions

General formula:

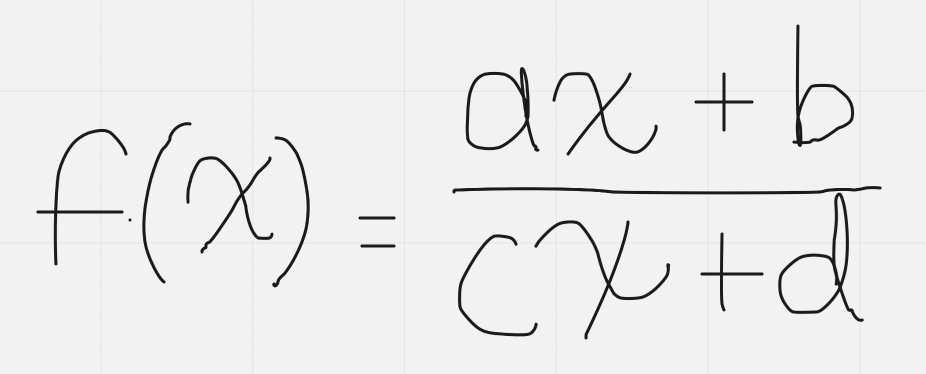
• There is an x in both the numerator and denominator now, still equal in degree though

Procedure

Rational Equations and Inequalities

Solving Rational Equations

• Clear your fractions: multiply, expand, solve

• Make one side = to another

• State restrictions, denominator ≠ 0

• Factor first

Solving Rational Inequalities (<,>,≤,≥ are inequality signs)

• Do not clear fractions

• Rearrange for 0 on one side

• Simplify to a single fraction: factor, common denominator

• Make an interval table

• Numerator → x intercept

• Denominator → vertical asymptote

Making an Interval Table

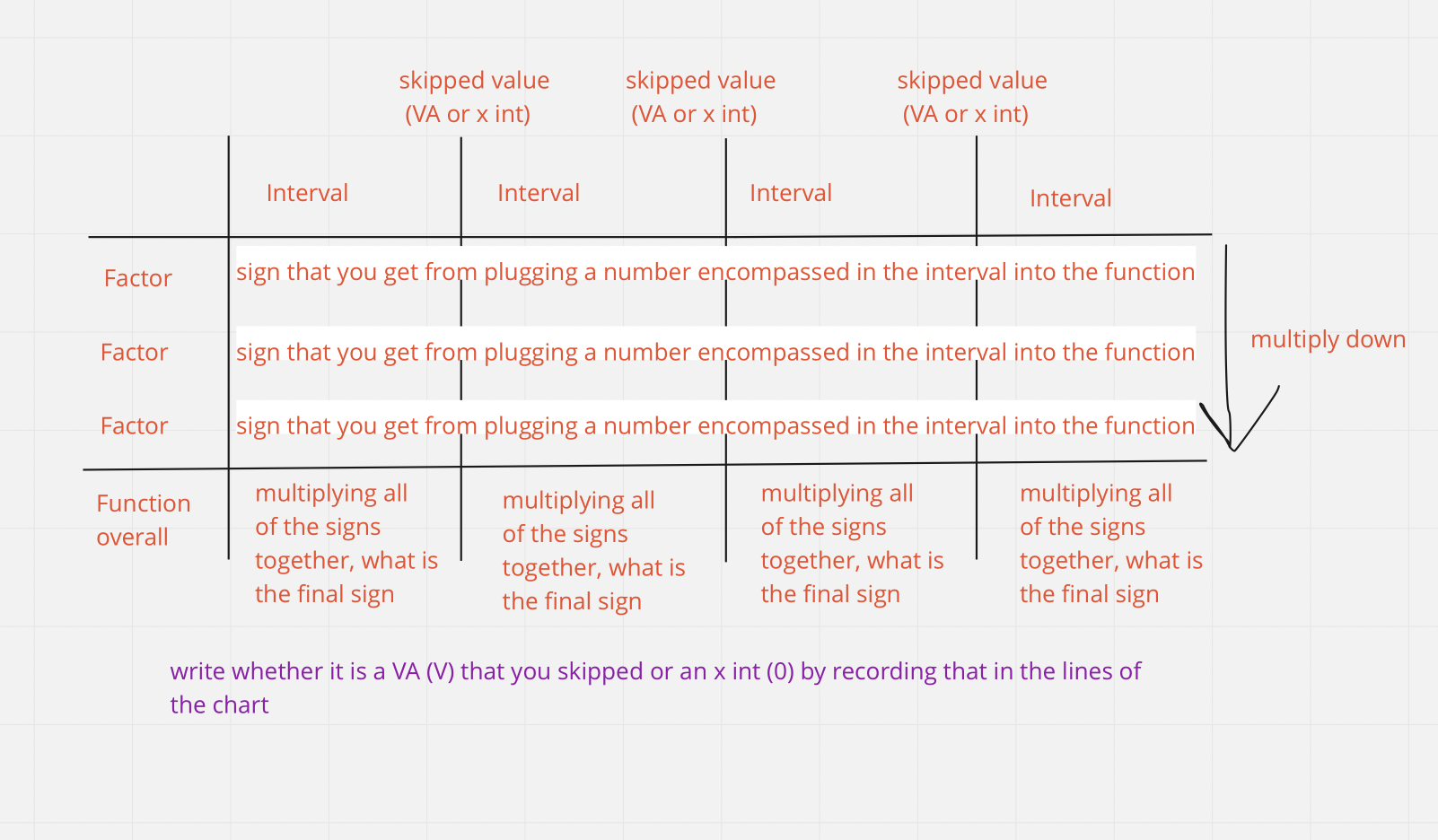
You can get Domain and Range from looking at the original question and seeing where it is positive/negative/positive and equal to 0/negative and equal to 0 from the interval table

• Look back to the original question and see what it is asking - then use the interval table to determine what is appropriate for the question

Special Cases

Holes

• Degree of the numerator is greater than the degree of the denominator

  • Always factor where you can

• Cancelled terms are what create holes

  • Restrict (make = to 0) the term that you’re cancelling - this is the x value of your hole’s coordinate → to find the y value of your hole, plug x into f(x) and solve

e.g.

• On a graph, holes are shown using an open circle at their point

Oblique Asymptote (OA)

Instead of an HA, essentially a slanted asymptote

Degree of the numerator is greater than the degree of the denominator

• Factor - see that nothing cancels and you don’t have a hole

• Carry out long division for polynomials

• Quotient (minus remainder if applicable) is the OA

  • y = OA

e.g.

Summary: Asymptote Rules for Rational Functions

VA: Set denominator to 0

HA:

1. Degree of numerator is less than degree of denominator → HA y=0

2. Degree of numerator is equal to degree of denominator → HA = y= a/c

OA:

Degree of numerator is greater than degree of denominator → not HA, OA is the quotient of polynomial division

Cancelled terms: make holes