7 Logarithmic Notation (Theory)

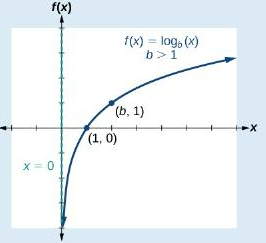
Basic Graph Shape of Logarithmic Functions when a > 1

Inverses of exponential graphs

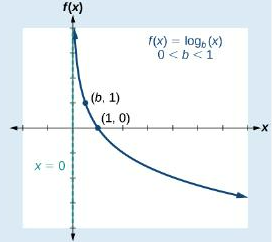
Basic Graph Shape of Logarithmic Functions 0 < a < 1

Inverses of exponential graphs

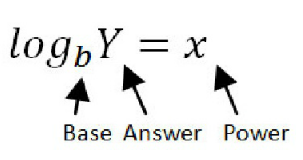
Parts of a Logarithmic Function

b - base

y - argument

x - power

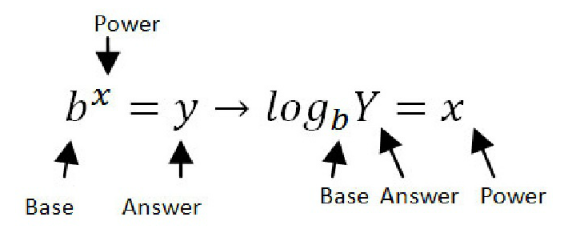
Translating Logs to Exponentials

Exponentials solve ______

Logarithms

Logarithms solve ______

Exponentials

Solving Logarithms

Step 1: Translate logarithm into an exponential

Step 2: Solve for x

How to Find the Inverse of Exponentials

Step 1: Write function in terms of y, substitute f(x) = y

Step 2: Switch x’s and y’s

Step 3: Solve for x in terms of y

Step 4: Write the exponential as a logarithm

Step 5: Rename y to f ^-1(x) = log_a (x)

Basic Graph Shape of Logarithmic Functions when a > 1 (Vertical Asymptote, Domain, Range, Key Points)

(1) Vertical Asymptote: x = 0

(2) Domain: (0, ∞)

(3) Range: (−∞, ∞)

(4) Key Points: (1, 0) and (a, 1)

Basic Graph Shape of Logarithmic Functions when 0 < a < 1 (Vertical Asymptote, Domain, Range, Key Points)

(1) Vertical Asymptote: x = 0

(2) Domain: (0, ∞)

(3) Range: (−∞, ∞)

(4) Key Points: (1, 0) and (a, 1)

Domain of Logarithms

argument > 0

can never be negatives, or equal to zero

Steps to Graphing Logarithmic Functions

Step 1: In order

Step 2: Key points
(1, 0) — inverse of exponential key points
(a, 1) — inverse of exponential key points

Step 3: Identify if a > 1, or if a < 1; predict the shape of your function whether it is always increasing or always decreasing

Step 4: Shifts
Horizontal shift
Vertical shift
Negatives (affect outputs of key points)
Constants (affect outputs of key points)

Step 5: T-Table to find true values
Use t-table
Pick points, plug into log, evaluate, and find true values

Product Property of Logarithms

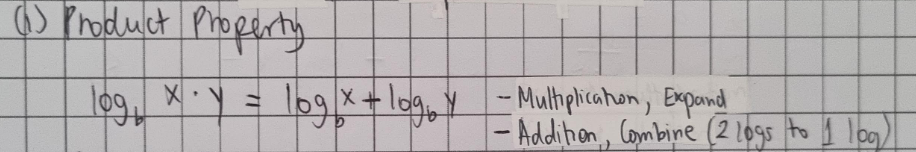
Quotient Property of Logarithms

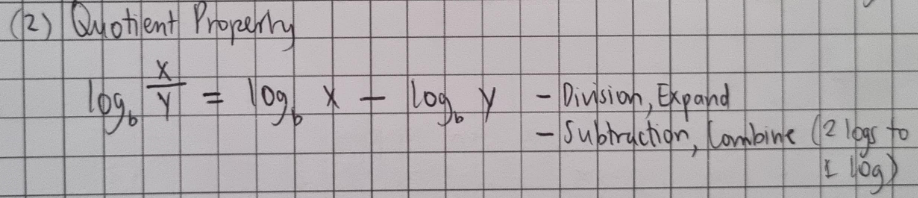
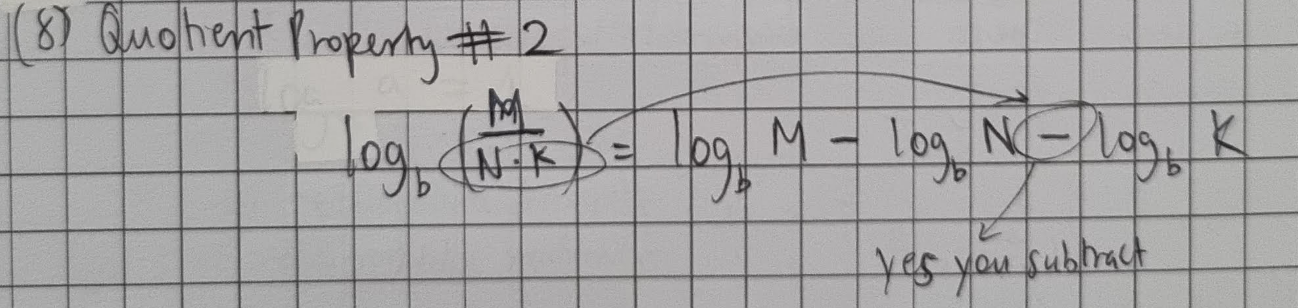
2ⁿ Quotient Property of Logarithms

Power Property of Logarithms

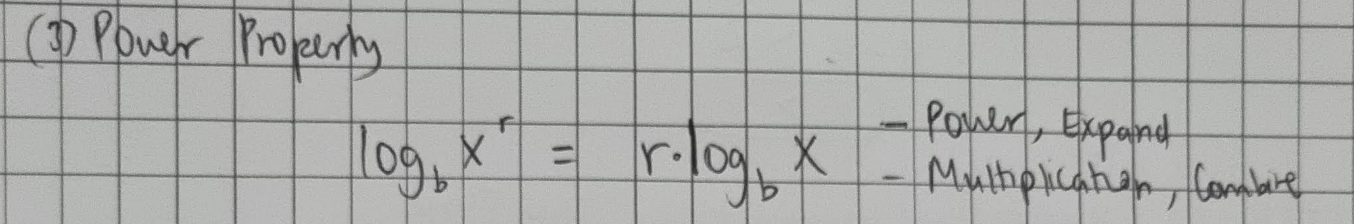
Zero Property of Logarithms

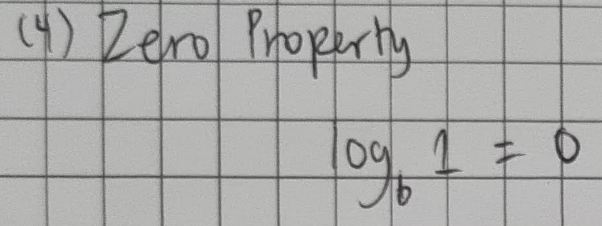
Identity Property of Logarithms

Inverse Property of Logarithms

Inverse Property of Exponents

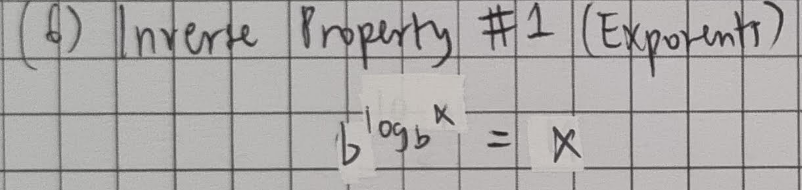
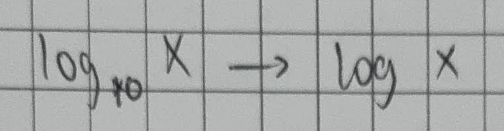
Common Logarithms

(1) logs with a base of 10

Natural Logarithms

(1) logs with a base of e

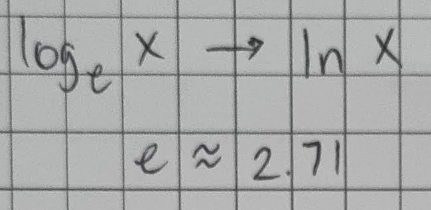
Change of Base Formula

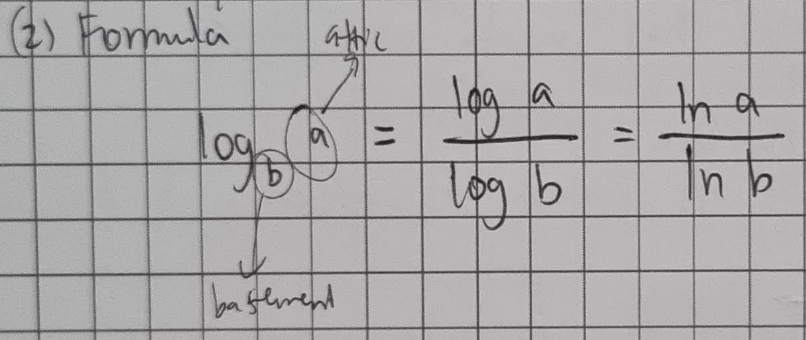
How does change of base work?

(1) allows you to change any log of any base into a base you want to work with

Solving Exponential and Logarithmic Equations — Exponential Form

Step 1: Simplify equation such that you have a power raised to a variable equal to a number (b^x = y)

Step 2: Check for common bases

Step 3: Take the common log of both sides

Step 4: Use the power property to move the exponent to the front of the logarithm

Step 5: Isolate the variable and solve for x

Solving Exponential and Logarithmic Equations — Logarithmic Form

Step 1: Simplify logs together to write as one log

Step 2: Convert logs to exponential

Step 3: Solve

negative logs do not exist