Вся теория по планиметрии

Условие существования треугольника?

Сумма любых двух сторон больше третьей

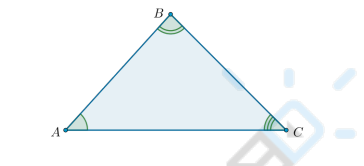
Сумма углов в треугольнике равна…

Сумма углов треугольника равна 180° .

∠A + ∠B + ∠C = 180°

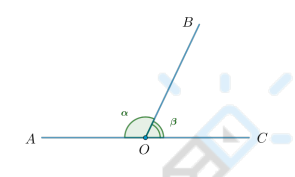
Что это за углы и каково их свойство?

Два угла, у которых одна сторона общая, а две другие являются продолжениями друг друга, называются смежными. Сумма смежных углов равна 180° .

∠AOB + ∠BOC = α + β =180°

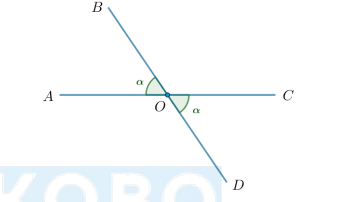
Что это за углы и каково их свойство?

Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого. Вертикальные углы равны.

∠AOB = ∠COD

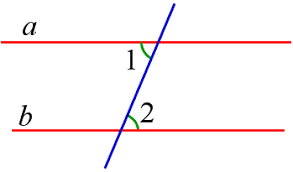
Что это за углы и каково их свойство?

если a ∥ b и c — секущая, то

∠1 = ∠2 (накрест лежащие углы)

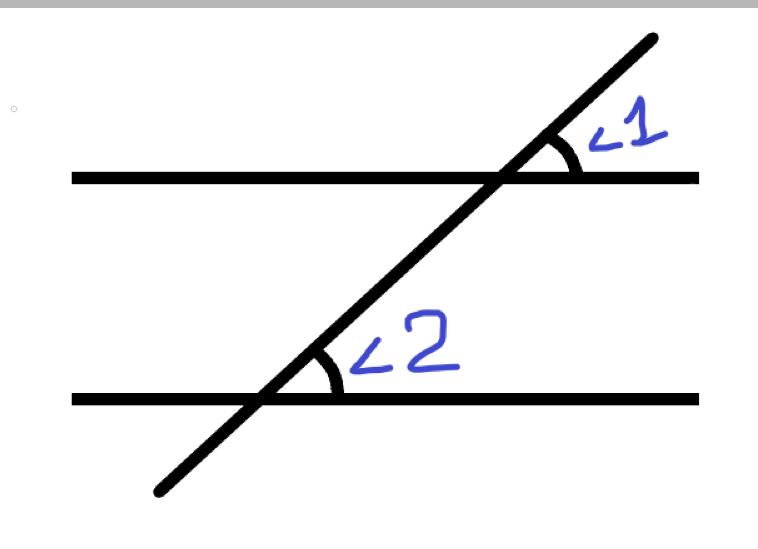
Что это за углы и каково их свойство?

если a ∥ b и c — секущая, то

∠1 = ∠2 (соответственные углы)

Что это за углы и каково их свойство?

если a ∥ b и c — секущая, то

∠1 + ∠2 = 180° (Внутренние односторонние углы)

В треугольнике напротив большей стороны…

Лежит больший угол

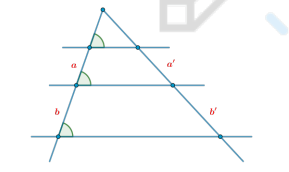
Прямая теорема Фалеса

Параллельные прямые высекают на сторонах угла пропорциональные отрезки:

a : b = a′ : b′

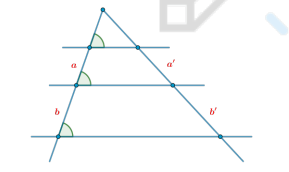
Обратная теорема Фалеса

Если прямые высекают пропорциональные отрезки на сторонах угла, то эти прямые параллельны.

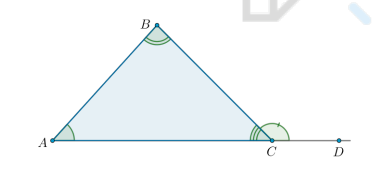
Что за ∠BCD и каково его свойство?

Внешним углом треугольника называется угол, смежный с каким-нибудь внутренним углом треугольника.

Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним.

∠BCD = 180° − ∠C =

= ∠A + ∠B

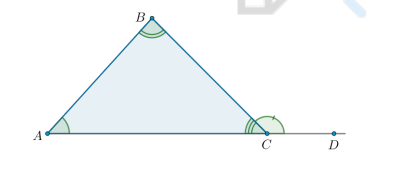
Какие есть признаки равенства треугольников?

1. По двум сторонам и углу между ними

2. По стороне и двум прилежащим к ней углам

3. По трем сторонам

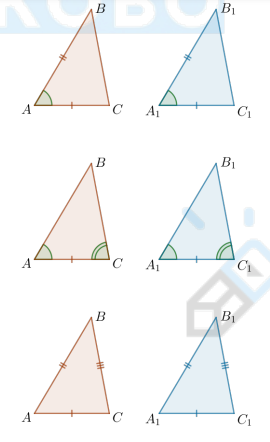
Что известно о средней линии треугольника?

Средняя линия треугольника — отрезок, соединяющий середины двух сторон треугольника.

1. Средняя линия треугольника равна половине третьей стороны и параллельна ей, то есть

   MN = 1/2 * AC и

   MN ∥ AC

2. Средняя линия треугольника отсекает от треугольника подобный ему треугольник:

   △MBN ∼ △ABC

3. Средние линии треугольника разбивают его на четыре равных треугольника:

   △₁ = △₂ = △₃ = △₄

   Следовательно, площади этих треугольников равны:

   S△₁ = S△₂ = S△₃ = S△₄

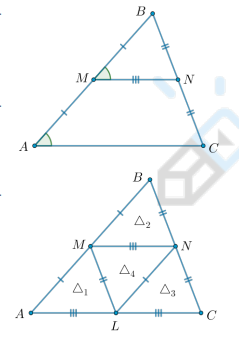
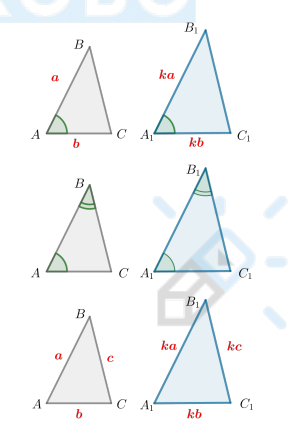
Какие есть признаки подобия треугольников?

Два треугольника называются подобными, если их углы соответственно равны, а стороны, лежащие напротив равных углов, относятся друг к другу с одним и тем же коэффициентом.

1. По отношению двух сторон и углу между ними

   Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы между ними равны, то такие треугольники подобны.

2. По двум углам

   Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.

3. По отношению трех сторон

   Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.

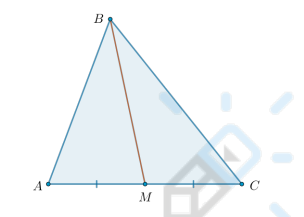
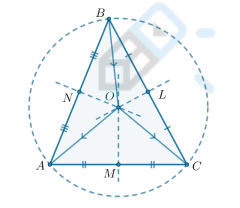
Чем является BM?

Ответ: Медианой.

Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника.

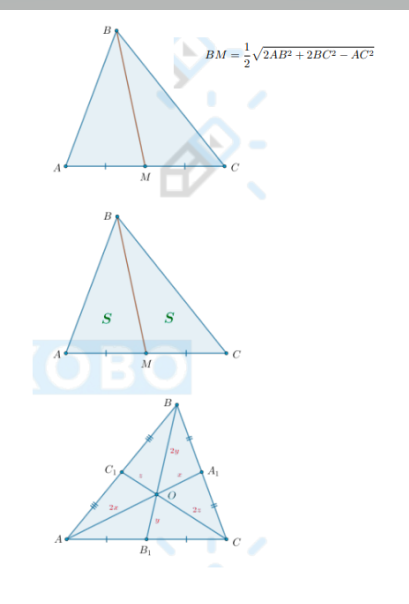
Что известно о медиане треугольника?

1. Формула длины медианы треугольника на картинке

2. Медиана и площади

   Медиана треугольника делит его на два треугольника, равных по площади (равновеликих):

   S△ABM = S△CBM

3. Точка пересечения медиан

   Медианы треугольника пересекаются в одной точке и точкой пересечения делятся в отношении 2 : 1, считая от вершины:

   AO : OA1 = BO : OB1= = CO : OC1 = 2 : 1

   При этом площади шести образовавшихся треугольников равны:

   SAOB1 = SCOB1 = SCOA1 = SBOA1 = SBOC1 = SAOC1

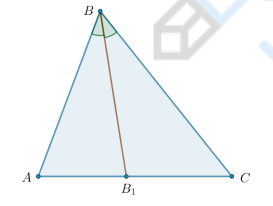
Чем является BB1?

Ответ: Биссектрисой.

Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны, называется биссектрисой треугольника.

Напомним, что биссектрисой угла называется луч, исходящий из вершины угла и делящий его на два равных угла.

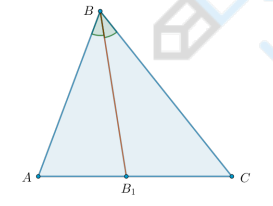
Что известно о биссектрисе треугольника?

Ответ находится в картинке

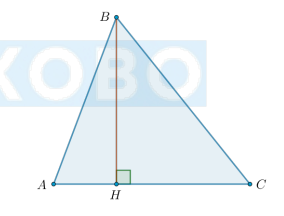
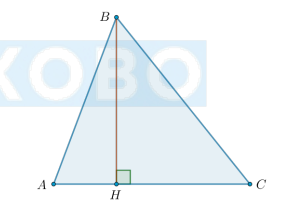
Чем является BH?

Ответ: Высотой.

Перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону, называется высотой треугольника.

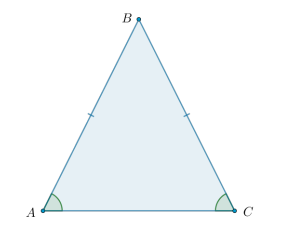
Что такое равнобедренный треугольник?

Треугольник называется равнобедренным, если две его стороны равны. Равные стороны называются боковыми сторонами, а третья сторона — основанием равнобедренного треугольника.

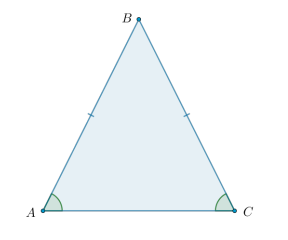
Каковы признаки равнобедренного треугольника?

1. Если в треугольнике равны два угла, то он равнобедренный.

2. Если в треугольнике биссектриса совпадает с медианой, то он равнобедренный.

3. Если в треугольнике медиана совпадает с высотой, то он равнобедренный.

4. Если в треугольнике высота совпадает с биссектрисой, то он равнобедренный.

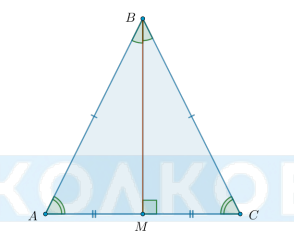
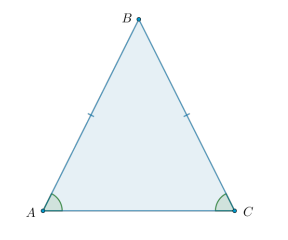
Каковы свойства равнобедренного треугольника?

1. В равнобедренном треугольнике углы при основании равны.

2. В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.

3. Высота равнобедренного треугольника, проведенная к основанию, является медианой и биссектрисой.

4. Медиана равнобедренного треугольника, проведенная к основанию, является высотой и биссектрисой.

Что такое прямоугольный треугольник?

Прямоугольный треугольник — это треугольник, в котором один угол прямой, то есть 90° .

∠C = 90° = ∠A + ∠B

Гипотенуза — это сторона прямоугольного треугольника, лежащая напротив прямого угла.

Катеты — это стороны прямого угла в прямоугольном треугольнике.

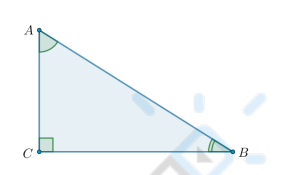
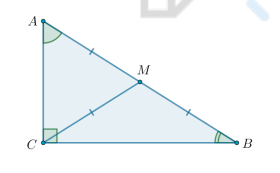
Что известно о медиане прямоугольного треугольника?

Медиана треугольника, проведенная из вершины прямого угла, равна половине гипотенузы:

CM = 1/2 * AB = AM = MB

Таким образом, получаются два равнобедренных треугольника:

△AMC и △CMB - р/б.

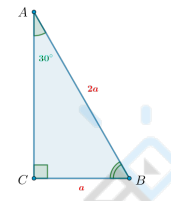
Что известно о прямоугольном треугольнике с углом в 30 градусов?

Катет, лежащий напротив угла 30◦ , равен половине гипотенузы.

Если катет равен половине гипотенузы, то он лежит напротив угла 30◦ .

Теорема Пифагора

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов:

c² = a² + b²

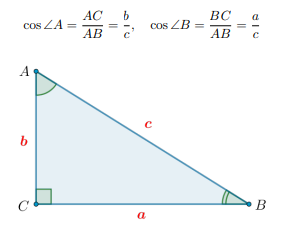
Что такое косинус острого угла прямоугольного треугольника?

Косинусом острого угла прямоугольного треугольника называется отношение длины прилежащего к этому углу катета к длине гипотенузы.

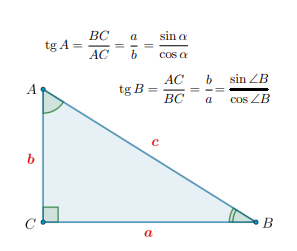
Что такое тангенс острого угла прямоугольного треугольника?

Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего этому углу катета к прилежащему.

Также тангенс острого угла прямоугольного треугольника равен отношению синуса этого угла к косинусу этого угла.

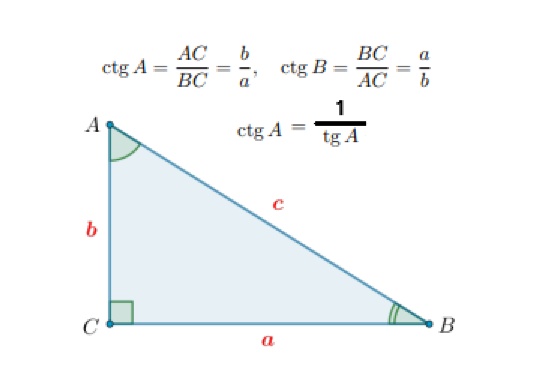
Что такое котангенс острого угла прямоугольного треугольника?

Котангенсом острого угла прямоугольного треугольника называется отношение прилежащего к этому углу катета к противолежащему.

Котангенс острого угла прямоугольного треугольника обратно пропорционален тангенсу этого угла.

Основное тригонометрическое тождество

sin²α + cos²α = 1

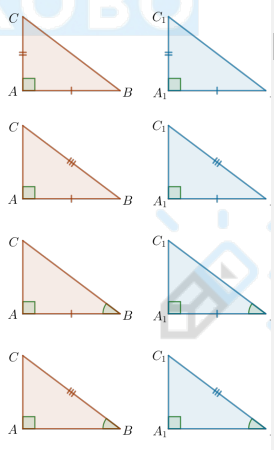
Какие есть признаки равенства прямоугольных треугольников?

1. По двум катетам

   Если катеты одного прямоугольного треугольника соответственно равны катетам другого, то такие треугольники равны.

2. По катету и гипотенузе

   Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого, то такие треугольники равны.

3. По катету и острому углу

   Если катет и прилежащий (противолежащий) к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему (противолежащему) к нему острому углу другого, то такие треугольники равны.

4. По гипотенузе и острому углу

   Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого, то такие треугольники равны.

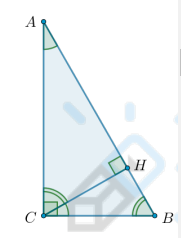
Что известно о высоте прямоугольного треугольника?

1. Высота из вершины прямого угла треугольника делит его на два треугольника, подобных исходному:

   △ABC ∼ △AHC ∼ △BHC

2. Квадрат высоты из прямого угла треугольника равен произведению длин отрезков, на которые она делит гипотенузу:

   CH² = AH · BH

3. Высота из прямого угла треугольника равна произведению длин катетов, деленному на длину гипотенузы:

   CH = AC · BC / AB

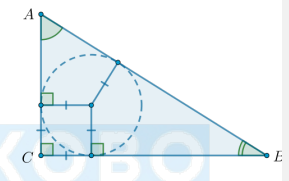
Что известно о вписанной окружности в прямоугольном треугольнике?

Вершина прямого угла, точки касания вписанной окружности и катетов и центр вписанной окружности прямоугольного треугольника образуют квадрат.

Что такое параллелограмм?

Параллелограмм — четырехугольник, у которого противоположные стороны попарно параллельны.

Какие есть признаки параллелограмма?

Четырехугольник является параллелограммом, если

1. противоположные стороны попарно равны.

2. две стороны равны и параллельны.

3. диагонали точкой пересечения делятся пополам.

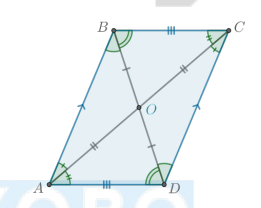
Какие есть свойства параллелограмма?

1. противоположные стороны попарно равны и параллельны.

2. противоположные углы попарно равны.

3. диагонали точкой пересечения делятся пополам.

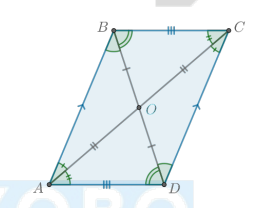
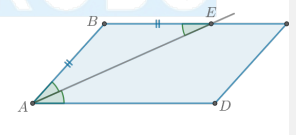
Что будет, если провести биссектрису угла параллелограмма?

Биссектриса AE параллелограмма ABCD отсекает от него равнобедренный треугольник, то есть

AB = BE

и

∠BAE = ∠DAE = ∠BEA.

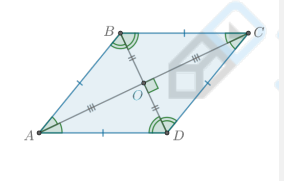
Что такое ромб?

Ромб — четырехугольник, у которого все стороны равны. Всякий ромб является параллелограммом.

Соответственно, ромб обладает всеми свойствами параллелограмма.

Какие есть признаки ромба?

Параллелограмм является ромбом, если

1. диагонали взаимно перпендикулярны.

2. диагонали являются биссектрисами его углов.

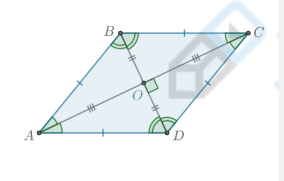
Какие есть свойства ромба?

1. диагонали взаимно перпендикулярны.

2. диагонали являются биссектрисами его углов.

3. все свойства параллелограмма

Что такое прямоугольник?

Прямоугольник — параллелограмм, у которого хотя бы один угол прямой.

Соответственно, прямоугольник обладает всеми свойствами параллелограмма.

Какие есть признаки прямоугольника?

Признаки прямоугольника:

1. Если у выпуклого четырехугольника все углы прямые, то он является прямоугольником.

2. Если у параллелограмма диагонали равны, то он является прямоугольником.

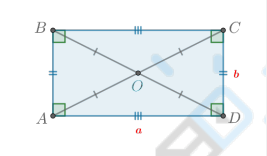
Какие есть свойства прямоугольника?

Свойства прямоугольника:

1. Диагонали прямоугольника равны.

2. Все свойства параллелограмма

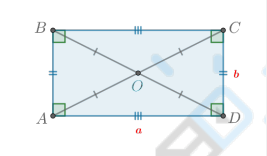
Что такое квадрат?

Квадрат — прямоугольник, у которого все стороны равны.

Альтернативное определение: квадрат — это ромб, у которого хотя бы один угол прямой.

Соответственно, квадрат обладает всеми свойствами прямоугольника и ромба.

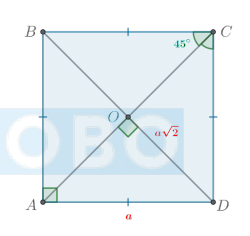
Какие есть свойства квадрата?

Свойства квадрата:

1. Все стороны равны.

2. Все углы прямые.

3. Диагонали точкой пересечения делятся пополам.

4. Диагонали равны.

5. Диагонали взаимно перпендикулярны.

6. Диагонали делят углы квадрата пополам.

7. Диагональ квадрата со стороной a равна a√2.

Что такое трапеция?

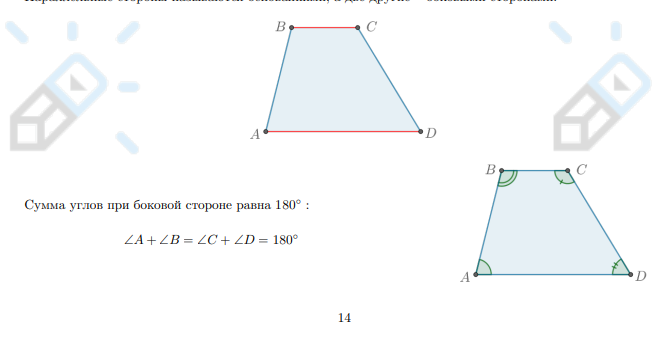
Трапеция — это выпуклый четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны.

Параллельные стороны называются основаниями, а две другие — боковыми сторонами.

Сумма углов при боковой стороне равна 180°:

∠A + ∠B = ∠C + ∠D = 180°

Что такое равнобедренная трапеция?

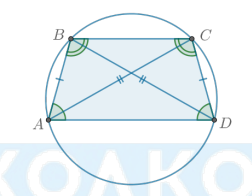
Если боковые стороны трапеции равны, то она называется равнобедренной.

Какие есть свойства равнобедренной трапеции?

Свойства равнобедренной трапеции:

1. В равнобедренной трапеции углы при любом основании равны.

2. В равнобедренной трапеции длины диагоналей равны.

3. Около равнобедренной трапеции можно описать окружность.

Какие есть признаки равнобедренной трапеции?

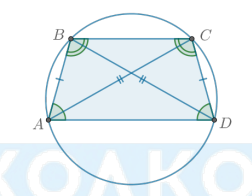
Признаки равнобедренной трапеции:

1. Если в трапеции равны углы при основании, то она равнобедренная.

2. Если диагонали трапеции равны, то она равнобедренная.

3. Если трапецию можно вписать в окружность, то она равнобедренная.

Сумма внутренних углов любого выпуклого n-угольника равна …

(n − 2) · 180°

Правильный многоугольник - это …

многоугольник, у которого все стороны равны и все углы равны.

Каждый угол правильного n-угольника равен …

(n − 2) · 180° / n

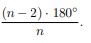
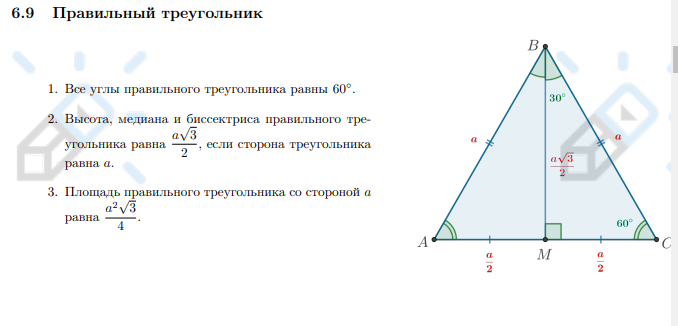
Что известно о правильном треугольнике?

1. Все углы правильного треугольника равны 60◦ .

2. Высота, медиана и биссектриса правильного треугольника равна a√3 / 2 , если сторона треугольника равна a.

3. Площадь правильного треугольника со стороной a равна a²√3 / 4 .

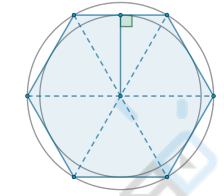
Что известно о правильном шестиугольнике?

1. Большие диагонали делят его на 6 равных равносторонних треугольников.

2. Большая диагональ в два раза больше стороны.

3. Центры вписанной и описанной окружностей совпадают — это точка пересечения больших диагоналей.

4. Радиус описанной окружности равен стороне.

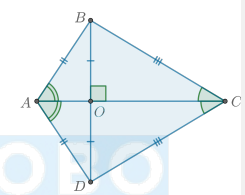
Что такое дельтоид?

Дельтоид — четырёхугольник, четыре стороны которого можно сгруппировать в две пары равных смежных сторон.

Какие свойства дельтоида?

Свойства дельтоида:

1. Диагонали взаимно перпендикулярны.

2. В любой выпуклый дельтоид можно вписать окружность.

3. Точка пересечения диагоналей делит одну из них пополам, а другая диагональ является биссектрисой углов и делит дельтоид на два равных треугольника.

Формула Герона?

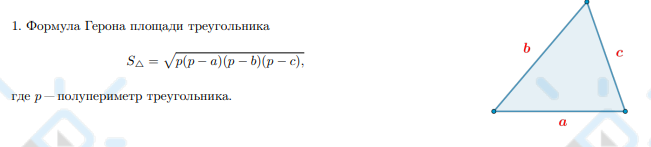
Какие есть формулы площади треугольника?

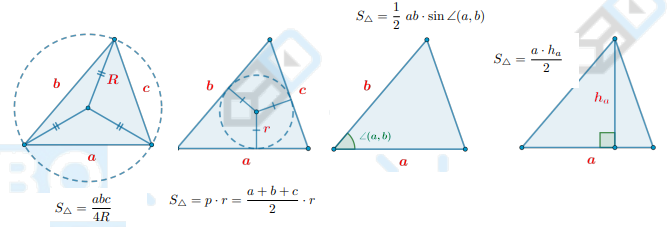
Как относятся площади треугольников, имеющих общую сторону?

Площади треугольников, имеющих общую сторону, относятся как высоты, проведенные к этой стороне:

Как относятся площади треугольников, имеющих общий угол?

Площади треугольников, имеющих общий угол, относятся как произведения сторон, образующих этот угол:

Как относятся площади треугольников, имеющих общую высоту?

Площади треугольников, имеющих общую высоту, относятся как основания, к которым эта высота проведена:

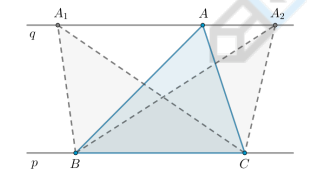
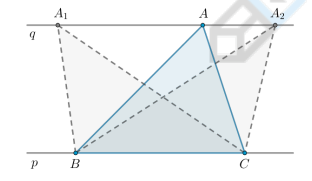
Если прямые p и q параллельны, то …

S△ABC = S△A₁BC = S△A₂BC

Отношение площадей подобных треугольников равно …

Отношение периметров подобных треугольников равно …

Отношение площадей подобных треугольников равно квадрату коэффициента подобия.

Отношение периметров подобных треугольников равно коэффициенту подобия.

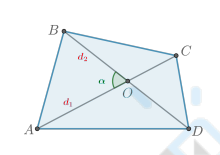
Площадь выпуклого четырехугольника равна …

Площадь выпуклого четырехугольника равна полупроизведению диагоналей и синуса угла между ними:

Какие есть формулы площади параллелограмма?

Площадь параллелограмма равна произведению высоты и стороны, к которой она проведена.

Площадь параллелограмма равна произведению сторон и синуса угла между ними.

Площадь параллелограмма равна полупроизведению диагоналей и синуса угла между ними.

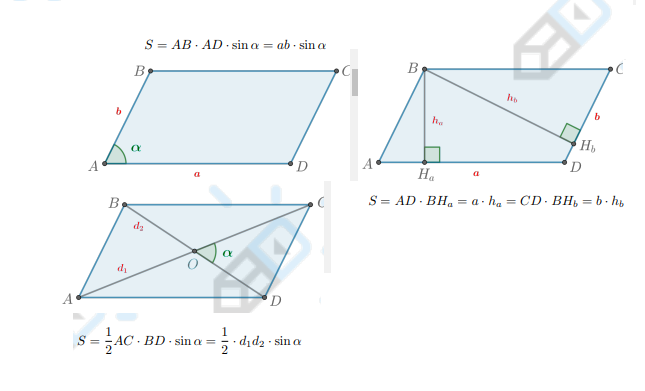
Какие есть формулы площади ромба?

Так как ромб — это параллелограмм, то его площадь можно найти с помощью любой формулы, справедливой для параллелограмма.

Какие есть формулы площади прямоугольника?

Все формулы для нахождения площади параллелограмма

Какие есть формулы площади квадрата?

Все формулы для нахождения площади прямоугольника и ромба

Формула площади трапеции?

Площадь трапеции равна произведению высоты и средней линии (полусуммы оснований).

Формула Брахмагупты?

Дан вписанный четырехугольник ABCD, p — его полупериметр. Тогда площадь четырехугольника:

Центральный угол - это …

Градусная мера дуги …

Вписанный угол - это …

1. Центральным углом

   называется угол с вершиной в центре окружности. Пусть точки A и B лежат на окружности с центром в точке O. Тогда угол AOB — центральный.

2. Градусная мера дуги

   Пусть ∠AOB = α. Градусной мерой дуги AB будем называть градусную меру центрального угла, который опирается на эту дугу.

   Тогда ⌣ AB = α.

3. Вписанным углом

   называется угол, вершина которого лежит на окружности, а его стороны пересекают эту окружность. Угол ACB — вписанный.

   Все вписанные углы, опирающиеся на дугу AB, равны половине центрального угла, опирающегося на эту дугу.

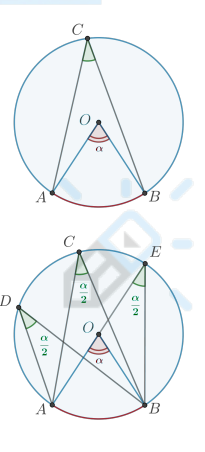
Свойства вписанных углов …

1. Вписанные углы, опирающиеся на одну и ту же дугу, равны.

2. Вписанный угол, опирающийся на диаметр окружности, равен 90°

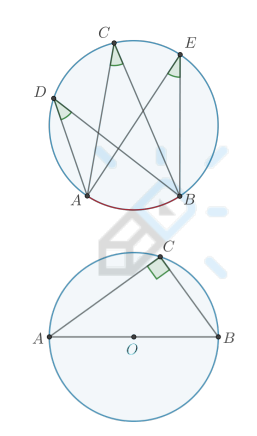
Чему равен угол между радиусом и касательной к окружности?

90°

Радиус, проведенный в точку касания, перпендикулярен касательной.

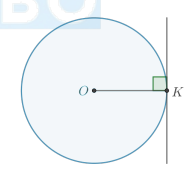
Свойства касательных к окружности …

Отрезки касательных к окружности, проведенных из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.

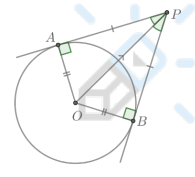
Где находится центр вписанной окружности треугольника?

Биссектрисы треугольника пересекаются в одной точке — центре вписанной окружности этого треугольника

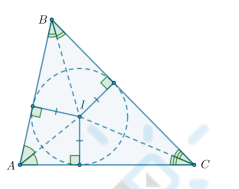
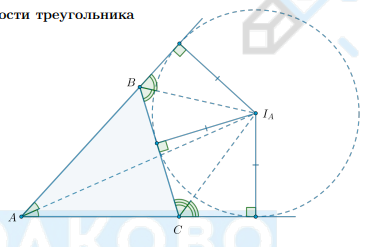
Где находится центр вневписанной окружности треугольника?

Центр вневписанной окружности треугольника лежит на пересечении внутренней биссектрисы угла треугольника, в который вписана окружность, и внешних биссектрис двух других углов.

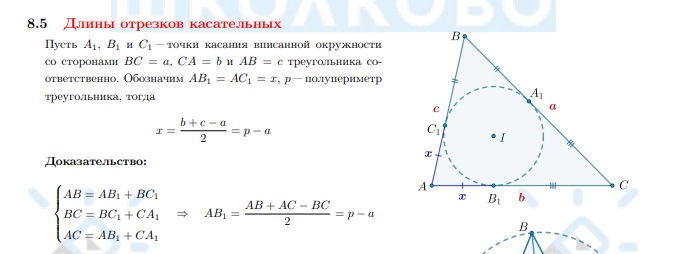
Длина отрезка касательной равна …

+ Доказательство

Где находится центр описанной окружности треугольника?

Серединные перпендикуляры треугольника пересекаются в одной точке — центре описанной окружности этого треугольника.

Что такое вписанный четырехугольник?

Вписанный четырехугольник — это четырехугольник, все вершины которого лежат на одной окружности.

Какие есть признаки вписанного четырехугольника?

Признак №1

Если сумма противоположных углов четырехугольника равна 180° , то вокруг него можно описать окружность.

Признак №2

Если в четырехугольнике углы, опирающиеся на одну сторону, равны, то он вписанный.

Признак №3

Если угол четырехугольника равен углу, смежному с противолежащим, то он вписанный.

Признак №4

Если явно найдена точка, от которой равноудалены вершины четырехугольника, то он вписанный.

Признак №5

Частный случай. Если два угла по 90° опираются на одну сторону четырехугольника, то он вписанный.

Какие есть свойства вписанного четырехугольника?

Свойство №1

Сумма противоположных углов вписанного четырехугольника равна 180° .

Свойство №2

Если четырехугольник вписанный, то углы, опирающиеся на одну сторону, равны.

Свойство №3

Если четырехугольник вписанный, то его угол равен углу, смежному с противолежащим.

Площадь круга = …

Площадь сектора круга = …

Угол между пересекающимися хордами окружности равен …

Угол между пересекающимися хордами окружности равен полусумме дуг, заключенных между ними:

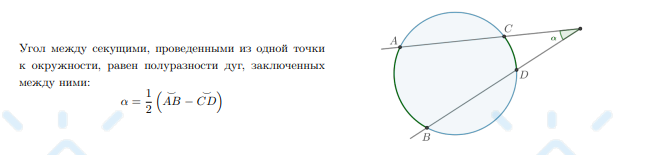
Угол между секущими, проведенными из одной точки к окружности, равен …

Угол между секущими, проведенными из одной точки к окружности, равен полуразности дуг, заключенных между ними:

Угол между хордой и касательной равен …

Угол между хордой и касательной равен вписанному углу, опирающемуся на дугу, отсеченную хордой.

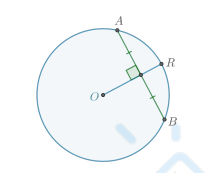
Если радиус перпендикулярен хорде, то …

Если радиус перпендикулярен хорде, то он делит ее пополам.

Верно обратное: если радиус делит хорду пополам, то он ей перпендикулярен.

OR ⊥ AB ⇔ OR делит AB пополам

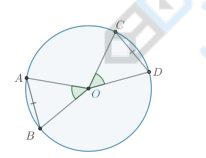
Равные хорды стягивают …

Равные хорды стягивают равные дуги. Верно обратное: равные дуги стягиваются равными хордами.

⌣ AB = ⌣ CD ⇔ AB = CD

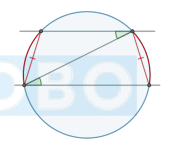
Если окружность пересекают две параллельные прямые, то …

Если окружность пересекают две параллельные прямые, то они высекают равные хорды.

Квадрат касательной равен…

квадрат касательной равен произведению секущей на ее внешнюю часть:

OK² = OB * OA

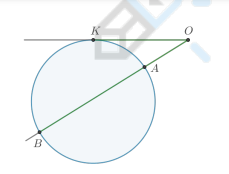
Свойство секущих проведенных из одной точки

OD * OC = OA * OB

Свойство отрезков пересекающихся хорд

произведения отрезков пересекающихся хорд равны

OC * OA = OD * OB

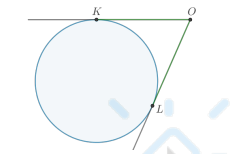
Отрезки касательных, проведенных из одной точки к окружности, …

Отрезки касательных, проведенных из одной точки к окружности, равны:

OK = OL

Центр вписанной в четырехугольник (многоугольник) окружности лежит …

Центр вписанной в четырехугольник (многоугольник) окружности лежит на пересечении биссектрис его углов.

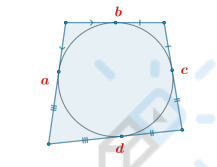
Свойство описанного четырехугольника

Если в четырехугольник можно вписать окружность, то суммы противоположных сторон четырехугольника равны.

Если суммы противоположных сторон четырехугольника равны, то в него можно вписать окружность.

a + c = b + d

9 Ортоцентр треугольника и его свойства

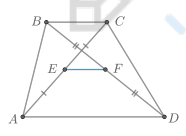
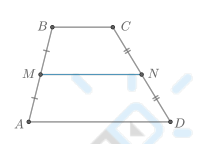
Что известно о средней линии трапеции?

Средняя линия трапеции — отрезок, соединяющий середины боковых сторон трапеции.

Она параллельна основаниям трапеции

и

равна их полусумме:

MN = 1 / 2 * (AD + BC)

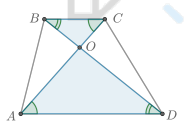
Что известно о треугольниках AOD и COB?

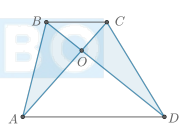
Что известно о треугольниках AOB и COD?

Треугольники AOB и COD равновелики.

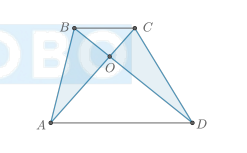
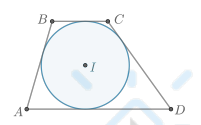
Свойство описанной трапеции

В трапецию можно вписать окружность, если сумма оснований трапеции равна сумме её боковых сторон:

AD + BC = AB + CD

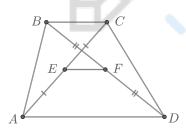
Отрезок, соединяющий середины диагоналей трапеции, равен …

Отрезок, соединяющий середины диагоналей трапеции, равен полуразности оснований:

EF = 1 / 2 (AD − BC)

Для доказательства этого факта достаточно провести среднюю линию трапеции, понять, что она содержит EF, и вычесть из нее длины средних линий треугольников ABC и DBC.