Kinematics

Key Ideas

Position(x): Where the object is present on the track.
Speed(y): How fast the object is moving.
Acceleration(a): How much the object’s speed changes in one second.
- When an object speeds up, acceleration is in the direction of its motion.
- When an object slows down, its acceleration is opposite the direction of motion.
Displacement (Δx) : how far the object ends up away from its starting point, regardless of any motion in between starting and ending positions.
The graphical analysis of motion includes position-time graphs and velocity-time graphs.
- Position-time graphs: The slope is the object’s speed, and the object’s position is read from the vertical axis
- Velocity-time graphs: the speed is read from the vertical axis, and the slope is the object’s acceleration
Free fall : No forces other than the object’s weight are acting on the object.
Projectile: object in free fall, but it isn’t falling in a straight vertical line.

Introduction to Motion in a Straight Line

All motion problems can be demonstrated with a cart on a track.
The motion detector can read the location of the cart up to 50 times each second.
This detector can make graphs of position or velocity versus time.

Goal of motion analysis is to describe, calculate, and predict:

where the cart is
how fast it’s moving
how much its speed is changing.

Graphical Analysis of Motion

Position-Time Graphs

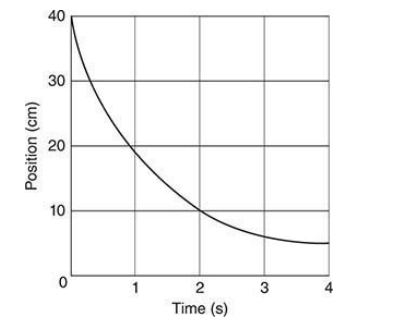
This graph represents the cart on the track.
Motion detector located at x=0.
Positive direction is towards the left.
In a position-time graph, the object’s position is read from the vertical axis.
In a position-time graph, the object’s speed is the slope of the graph.
- The steeper the slope, the faster the object moves.
- If the slope is a front slash (/), the movement is in the positive direction.
- If the slope is a backslash (\), the movement is in the negative direction

Velocity - Time Graphs

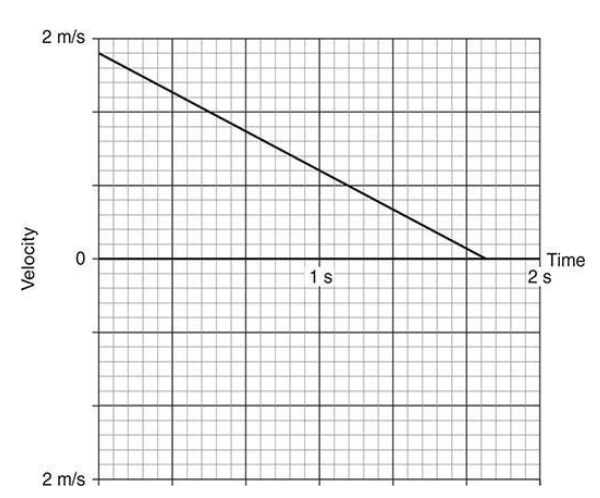
This velocity-time graph represents a different cart on the track.
The positive direction is to the left.
In a velocity-time graph, the object’s speed is read from the vertical axis.
The direction of motion is indicated by the sign on the vertical axis.
In a velocity-time graph, the object’s acceleration is the slope of the graph.
To calculate the amount of acceleration:
- use rise/run calculation or
- use the definition of acceleration to see that the object lost 1 m/s of speed in 1 second, making the acceleration 1 m/s per second
The object in the graph above is slowing down and moving to the left.
When an object slows down, its acceleration is opposite the direction of its motion.
In the graph above, this cart has an acceleration to the right.
Acceleration is not the same thing as speed or velocity.
- Acceleration says how quickly speed changes.
- Acceleration doesn’t say anything about which way something is moving, unless you know whether the thing is speeding up or is slowing down.
- Acceleration to the right means either speeding up and moving right, or slowing down and moving left.
The object’s displacement is given by the area between the graph and the horizontal axis.
Location of the object can’t be determined from a velocity-time graph.

Algebraic Analysis of Motion

When asked to analyze motion from a description and not a graph, start analysis by defining a positive direction and clearly stating the start and the end of the motion.
In any case of accelerated motion when three of the five principal motion variables are known, the remaining variables can be solved for using the kinematic equations.
The five principal motions are:
- initial velocity
- final velocity
- displacement
- acceleration
- time
To calculate the missing values in a motion chart, use the three kinematic equations listed as follows

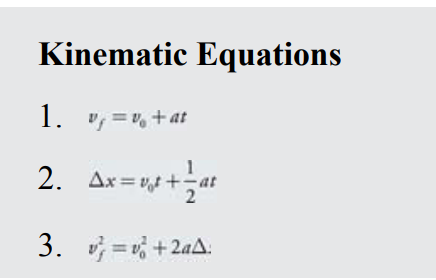Objects in Free Fall

When an object is in free fall, its acceleration is 10 m/s per second toward the ground.
Free fall means no forces other than the object’s weight are acting on the object.

Projectile Motion

A projectile is defined as an object in free fall.
But this object doesn’t have to be moving in a straight line.
If the object were launched at an angle, treat the horizontal and vertical components of its motion separately.
- A projectile has no horizontal acceleration and so moves at constant speed horizontally.
To approach a projectile problem, make two motion charts: one for vertical motion and one for horizontal motion.
- To find the vertical component of a velocity at an angle, multiply the speed by the sine of the angle.
- To find the horizontal component of a velocity at an angle, multiply the speed by the cosine of the angle. This always works, as long as the angle is measured from the horizontal.
The horizontal and vertical motion charts for a projectile must use the same value for time.

### Example

A model rocket is launched straight upward with an initial speed of 50 m/s. It speeds up with a constant upward acceleration of 2.0 m/s per second until its engines stop at an altitude of 150 m.

What if Acceleration isn't Constant?

The slope of a graph is related to the derivative of a function; the area under a graph is related to the integral of a function.
To find velocity from a position function, take the derivative with respect to time.
To find acceleration from a velocity function, also take the time derivative.
To find position from a velocity function, take the integral with respect to time.
To find velocity from an acceleration function, take the time integral.

Air Resistance and the First-Order Differential Equations

The force of air resistance is usually negligible in kinematics problems.
Air resistance is not important in kinematics.
Air resistance should only be considered when the problem explicitly says so.

Steps to Solve Air Resistance Problems

Find the terminal speed.

Terminal speed: after a long time, the object’s speed becomes constant.
To find that terminal speed, do an equilibrium problem.
Free body, set up forces equal down forces, and left forces equal right forces.
If something’s falling straight down with no other forces, usually you’ll get bv = mg.
Then solve for v. That’s the terminal speed.
1. Sketch a graph of the speed of the object as a function of time.

If the object was dropped from rest, or given an initial velocity, that point can be plotted at time t = 0.
Then find terminal velocity using the method —the terminal speed is the constant velocity after a long time.
Plot a horizontal line for the terminal velocity near the right-hand side of the t-axis.
1. Describe the motion in words, including what’s happening to the acceleration and/or the velocity
2. Solve a differential equation to find an expression for the velocity as a function of time