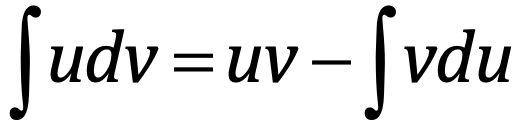Derivatives + Integrals

This is all the derivatives and integrals you should memorize for BC

Chain Rule ⋅

Chain Rule ⋅

(d/dx) f(g(x)) = f’(g(x)) ⋅ g’(x)

Product Rule ⋅

(d/dx) (f ⋅ g) = (f ⋅ g’) + (f’ ⋅ g)

Quotient Rule ⋅

(d/dx) (f/g) = ((g ⋅ f’) - (f ⋅ g’))/g²

Differentiation ⋅

The process of finding the derivative of a function, which measures how a function changes as its input changes.

⋅

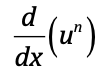
nu^(n-1) du/dx

⋅

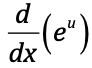
e^u du/dx

⋅

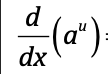
a^u ⋅ ln(a) du/dx

⋅

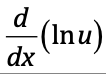
1/u du/dx

⋅

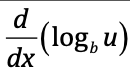
1/(u⋅ln(b)) du/dx

⋅

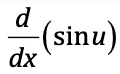
cos(u) du/dx

⋅

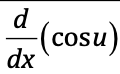
-sin(u) du/dx

⋅

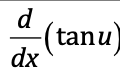
sec²u du/dx

⋅

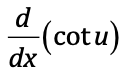
-csc²(u) du/dx

⋅

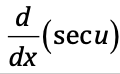
sec(u)tan(u) du/dx

⋅

cot(u)csc(u) du/dx

⋅

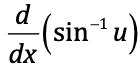
1/(sqrt(1-u²)) du/dx

⋅

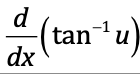
1/(1+u²) du/dx

⋅

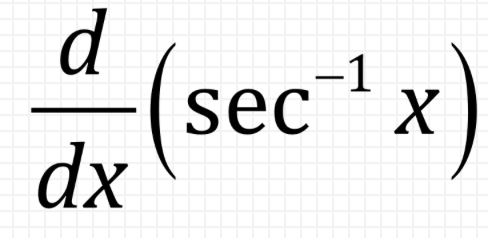
1/((u)(sqrt(1-u²))) du/dx

⋅

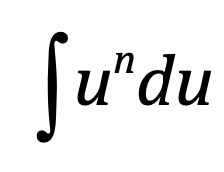
1/(n+1) ⋅ u^(n+1) + C

⋅

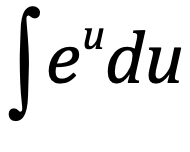
e^u + c

⋅

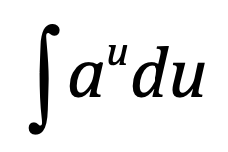
(a^u)/(ln(a)) + C

⋅

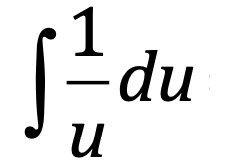
ln|u| + C

⋅

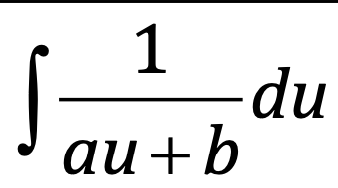
(1/a) ⋅ ln|au+b| + C

⋅

sin(u) + C

⋅

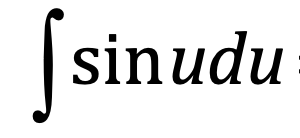
-cos(u) + C

⋅

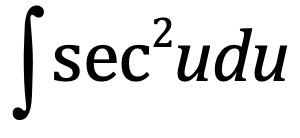
tan(u) + C

⋅

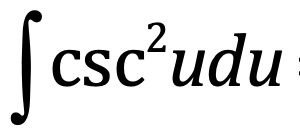
-cot(u) + C

⋅

sec(u) + C

⋅

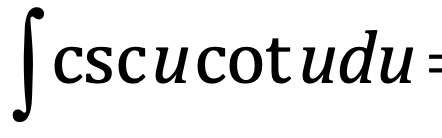
-csc(u) + C

⋅

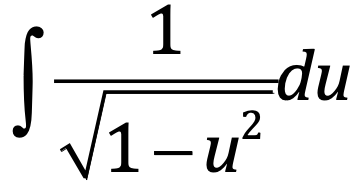
arcsin(u) + C

⋅

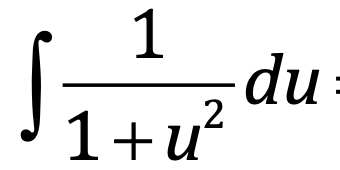
arctan(u) + C

⋅

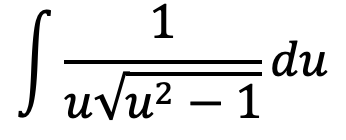
arcsec(u) + C

What does LIPET stand for?

Logarithms, Inverse Trig, Polynomials, Exponents, Trig

How do you do integration by parts?