Wave Optics - Interference

L4-5

magnitude of wavevector

k = 2π / λ

phase velocity

v = ω / k = c / n

Intensity (I)

Power per unit area (energy per unit area per unit time)

I is proportional to |𝜓|² = |A|²

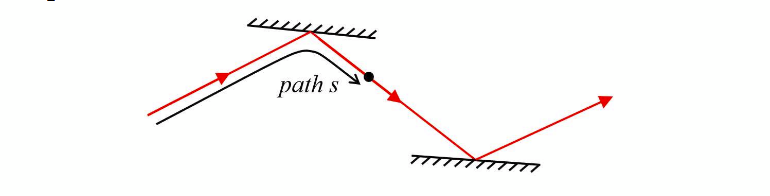
wave on an arbitrary path

(+c.c.)

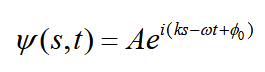
phase change after distance s at a given time t

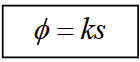
plane wave in an arbitrary direction

For a plane wave in a straight line, we can express 𝜓(r, t) at a point with position vector r = (x, y, z) by:

taking unit vector n in the direction of s.

Understanding that s is the component of r along the direction n expressed as: s = |r|cosθ = |r||n|cosθ = r . n

Then define wavevector k = kn = (k_x, k_y, k_z)

Then realise that ks = kr.n = k.r and substitute that into the original wave function. expand out to finally get the equation shown

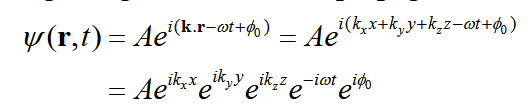
superposition principle

the disturbance (wave function 𝜓) at any point in a linear mediun is the algebraic sum of the two constituent waves

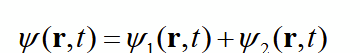
net disturbance of two waves

Intensity in the interference of two waves

I = |𝜓|² = 𝜓*𝜓 = I₁ + I₂ + 2sqrt(I₁I₂)cos(δΦ)

because cosz = (exp(iz) + exp(-iz)) / 2 and I = A²

relative phase (phase difference)

δΦ = Φ₂ - Φ₁

interference when I₁ = I₂

I = 2I₁ [1 + cosδΦ] = 4I₁cos²(δΦ/2)

final intensity can rang from 0 to double the sum of the original intensities.

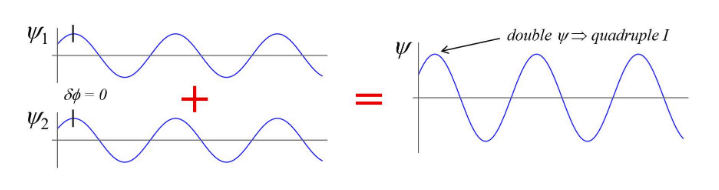
constructive interference

δΦ = 2mπ

I = 4I₁

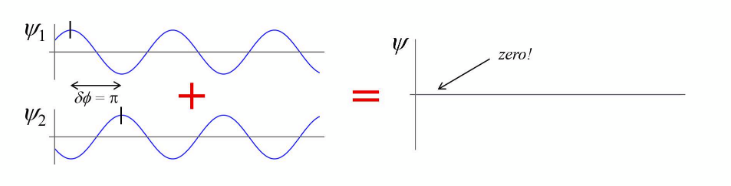
destructive interference

δΦ = 2(m + ½)π

I = 0

coherence

assume that δΦ is constant i.e. waves have the same frequency and are cut off from the same source so that δΦ₀ (phase offset) are correlated and not random (i.e. their average doesn’t g to 0)

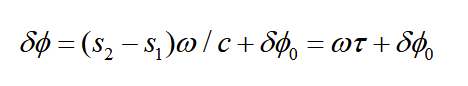
time delay

time delay between two coherent waves because they travel different distances s1 and s2

temporal coherence

real monochromatic light sources have small but finite spectral bandwidth δω. each value of ω has its own interference term, and we detect the average of cos(ωτ + δΦ₀). In order for coherence, τ_c = 2π/δω (so that δωτ = 2π for coherence.)

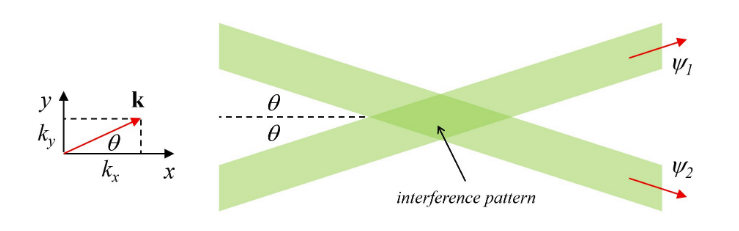
intensity of two angled plane waves at ±θ to x axis

I₀ = I₁ + I₂ = 2A²

we see a pattern of interference ‘fringes’ as I varies between destructive and constructive inteference with a pattern Δy = π/(k sinθ) because period of cos² is π

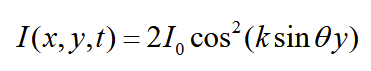
What do interference fringes show

that if there is destructive interference (I = 0) somewhere, there must also be constructive interference (I = 2I₀) somewhere else in order to conserve overall energy (<I> = I₀)

interferometer

a device that makes use of interference to measure something, using light split off from a single source.

Wavefront Interferometer: e.g. Young’s Double Slit

Bright fringes occur when argument is mπ (due to period of cos²) and fringe spacing is ΔX = λL/d

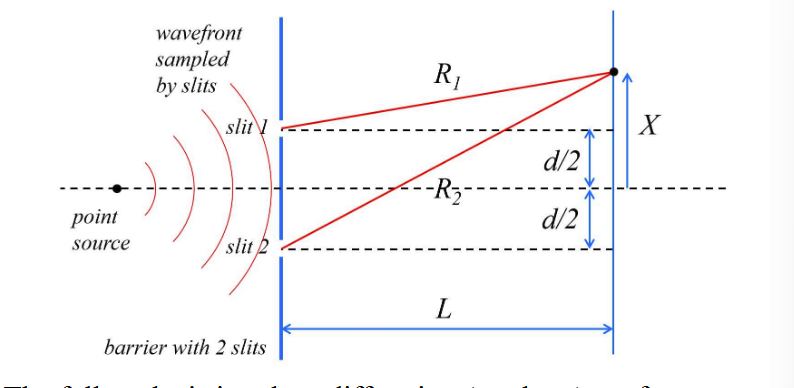
intensity in wavefront interferometer

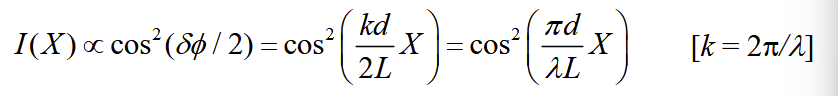
Amplitude-division Interferometer e.g. Michelson Interferometer

constructive interference at δΦ = 2mπ and destructive at 2(m+ ½)π.

δΦ = 4πΔL / λ

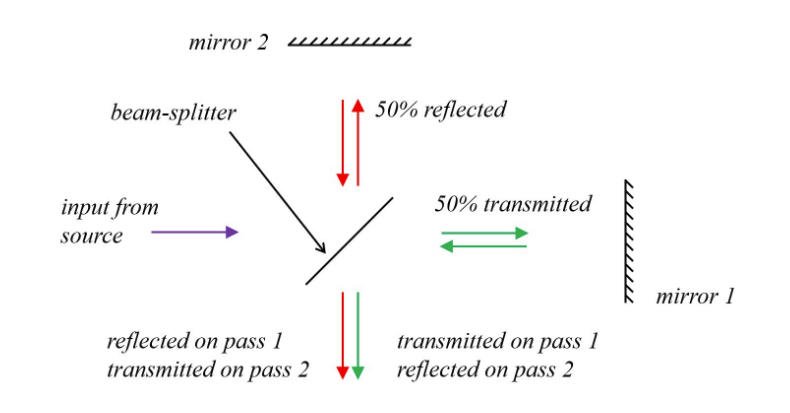
intensity on wave-front interferometer

I = I₀ = 4I₁ i.e. all of the incident light arrives at the output