MSE 2001 : Crystal Systems, Lattice Types, Bravais Lattice, and Crystal Structure

How many crystal systems, lattice types and bravais Lattices are there?

7 crystal systems, 4 lattice types, and 14 Bravais Lattices

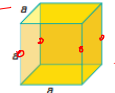
Cubic crystal system

a = b = c

α = B = y = 90°

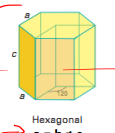
Hexagonal crystal system

a = b ≠ c

α = 120° , β = γ = 90°

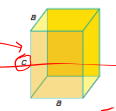
Tetragonal crystal system

a = b ≠ c

α = β = γ = 90°

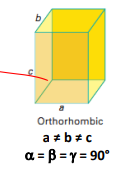
Orthorhombic crystal system

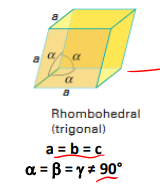
Rhombohedral (trigonal) crystal system

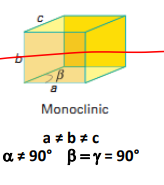
Monoclinic crystal system

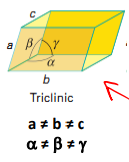
Triclinic crystal system

What are the abbreviations for each lattice type?

• Primitive/Simple

• Body Centered

• Base Centered

• Face Centered

• Primitive/Simple (P)

• Body Centered (I)

• Base Centered (C)

• Face Centered (F)

Primitive (simple) lattice type

Lattice points (atoms) at each corner

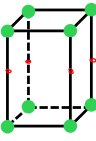
Body centered lattice type

Atoms at each corner + 1 atom in the center

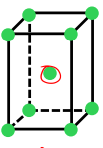
Base centered lattice type

Atoms at all each corner + 2 atoms centered on faces

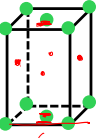
Face centered lattice type

Atoms at all corners + 6 atoms on faces (6 faces total, 1 atom per face)

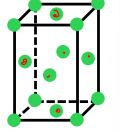
Cubic primitive Bravais lattice

a = b = c

α = B = y = 90°

atoms at all corners of the cube

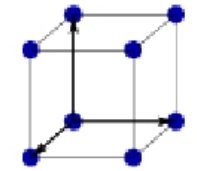
Cubic body-centered Bravais lattice

a = b = c

α = B = y = 90°

Atoms in corners + 1 atom in the center

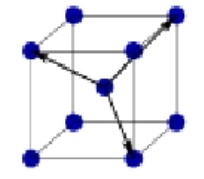
Hexagonal primitive Bravais lattice

a = b ≠ c

α = 120° , B = y = 90°

Atoms at all corners of unit cell

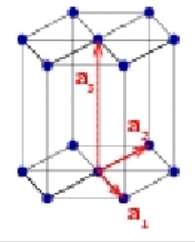
Tetragonal primitive Bravais lattice

a = b ≠ c

α = B = y = 90°

Atoms at all corners

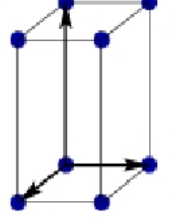
Tetragonal body-centered Bravais Lattice

a = b ≠ c

α = B = y = 90°

Atoms at all corners + 1 atom in the center

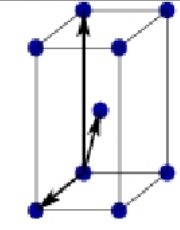
Orthorhombic primitive Bravais lattice

a ≠ b ≠ c

α = B = y = 90°

Atoms at all corners

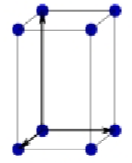
Orthorhombic body-centered Bravais lattice

a ≠ b ≠ c

α = B = y = 90°

Atoms at all corners + 1 atom in the center

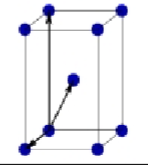
Orthorhombic base centered Bravais lattice

a ≠ b ≠ c

α = B = y = 90°

Atoms at all corners + 2 atoms (centered on each face)

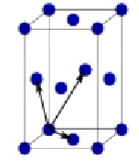
Orthorhombic face centered Bravais Lattice

a ≠ b ≠ c

α = B = y = 90°

Atoms at all corners + centered on each face (6 atoms total, 1 per face)

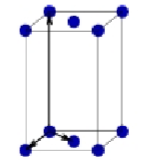
Rhombohedral (trigonal) primitive Bravais lattice

a = b = c

α = B = y ≠ 90°

Atoms at all corners

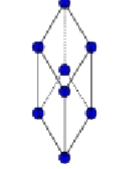
Triclinic primitive Bravais Lattice

a ≠ b ≠ c

α ≠ B ≠ Y

Atoms at all corners

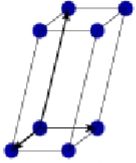
Monoclinic primitive Bravais lattice

a ≠ b ≠ c

α ≠ 90°

B = y = 90°

Atoms at all corners

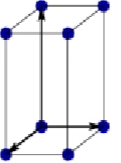
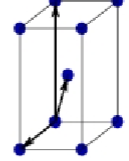
Monoclinic body-centered Bravais lattice

a ≠ b ≠ c

α ≠ 90°

B = y = 90°

Atoms at all corners + 1 atom in the center

Crystal structure “formula”

Crystal structure = Lattice + Basis

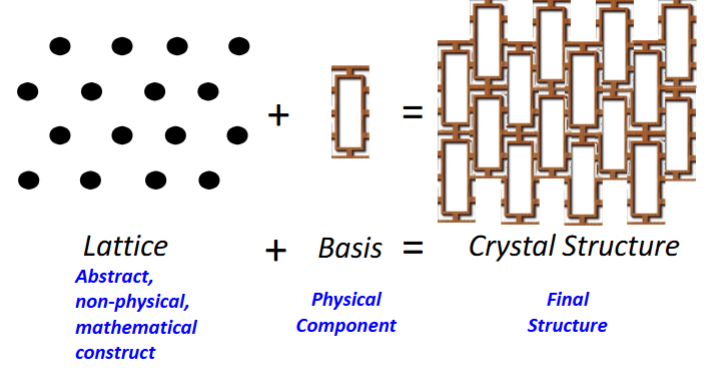
What is a lattice?

The place where we put things (map)

Lattice sites

What is a basis?

The stamps we put down

What we put on the lattice sites