MMW

Mathematics in the Modern World - EE

Pattern

is an arrangement that helps us anticipate what comes next.

Logic Patterns

The most basic patterns, involving classification and enumeration.

Word Patterns

Found in language, such as grammar rules (e.g., forming plurals, verb tenses) and sentence structure.

Geometric Patterns

Motifs or designs using abstract shapes like lines, polygons, and circles (e.g., wallpapers, tiles).

Number Patterns

Sequences of numbers governed by a specific rule (e.g., Pascal's Triangle).

Symmetries

is created by transformations, which move a figure without changing its size or shape.

Transformation

It is a correspondence where we can pair each point of a figure (object) with exactly one point of its image on a Euclidean plane and vice versa.

Reflection (Bilateral Symmetry)

Mirrors a figure across a line.

Rotation (Radial Symmetry)

Turns a figure around a central point.

Translation

Slides a figure a certain distance in a specific direction.

Glide Reflection

A combination of a translation and a reflection.

Rosette Patterns

Have rotation and/or reflection but no translation. They are fixed around a center point.

Rosette Pattern (Cyclic)

Only has rotational symmetry.

Rosette Pattern (Dyhedral)

Has both rotational and reflectional symmetry.

Frieze Patterns

Patterns that repeat in a single direction.

Mathematician John Conway

Created the 7 names relating to footsteps

Footstep - Hop

This pattern only involves translation. (f)

Footstep - Step

It is also called glide reflection symmetry (f)

Footstep - Siddle

It consists of translation and vertical reflection (f)

Footstep - Spinning hop

It contains translation and rotation (by a half-turn or rotation 180° angle) symmetries (f)

Footstep - Spinning Siddle

It contains translation, glide reflection and rotation (by a half-turn) symmetries (f)

Footstep - Jump

It contains translation and horizontal reflection symmetries (f)

Footstep - Spinning Jump

It contains all symmetries (translation, horizontal & vertical reflection, and rotation). (f)

Wallpaper Patterns

Patterns that repeat in two different directions, covering an entire plane. There are 17 distinct types.

Tessellations (Tiling)

Patterns of repeating figures that cover a plane without any gaps or overlaps, like a honeycomb.

Tessera

the latin word that tesselation comes from and means "Square tablet"

Fibonacci Sequence

A sequence where each number is the sum of the two preceding ones. It starts: 0, 1, 1, 2, 3, 5, 8, 13, 21, ...

Leonardo of Pisa

Creator of Fibonacci Sequence

(1180-1250)

Time where fibonacci sequence is created

Golden Ratio (ϕ)

An irrational number approximately equal to 1.618.

1.618

The ratio of successive Fibonacci numbers gets closer and closer to the Golden Ratio.

P1

pg

pgg

pm

cm

cmm

pmg

p2

p4

p4m

p4g

p3

p3m1

p31m

p6

p6m

pmm

Language

is a systematic means of communicating by the use of of sounds or conventional symbols. and a code humans use as a form of expressing themselves and communicating with others.

Language components

vocabulary, grammar, community of people, range of meaning

Noun

name given to object of interest

Sentence

must state a complete thought

Expression

name given to mathematical object of interest

Precise

It can make very fine distinctions or definition among set of mathematical symbols. That is, it removes all ambiguity.

Concise

It can express otherwise long exposition or sentence briefly using language of mathematics. That is, it says alot with very little

Powerful

One can express complex thoughts with relative ease

Preposition

is a declarative that is either true or false, but not both.

Simple preposition

is a preposition that conveys one thought with no connecting words.

Compound preposition

is a preposition containing (declarative) sentences that are combined together with connecting words.

Tautology

is a statement that is always true

Self-contradiction

is a statement that is always false

Existential Quantifiers

The word some and the phrases there exist and at least one

Universal Quantifiers

The word none, no, all and every

Negation

not p, ¬ p

Conjunction

p and q, p∧q

Disjunction

p or q, p∨q

Conditional

if p, then q, p ⇒ q

Biconditional

p if and only if q, p ⇔ q

Negation

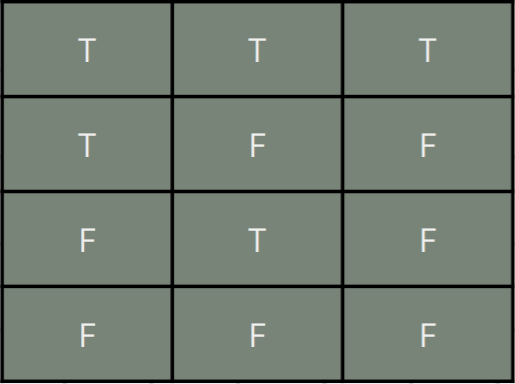
Conjunction

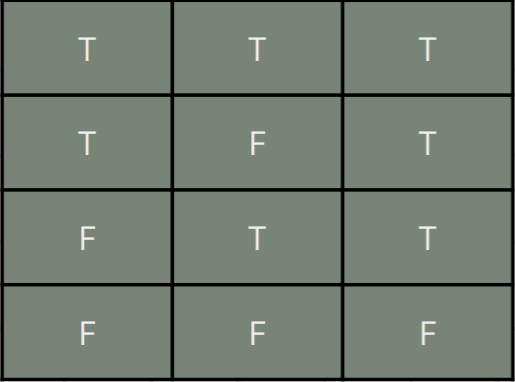
Disjunction

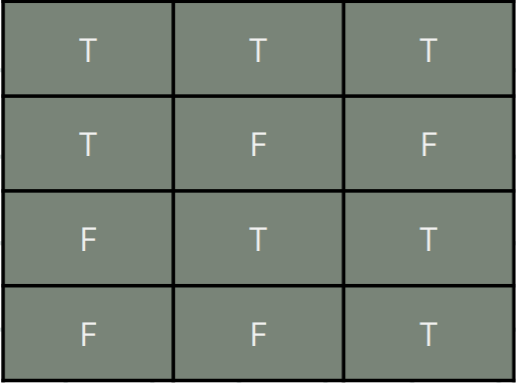
Conditional

Converse

p ⇒ q is q ⇒ p

Inverse

p ⇒ q is ¬p ⇒ ¬q

Contrapositive

p ⇒ q is ¬q ⇒ ¬p

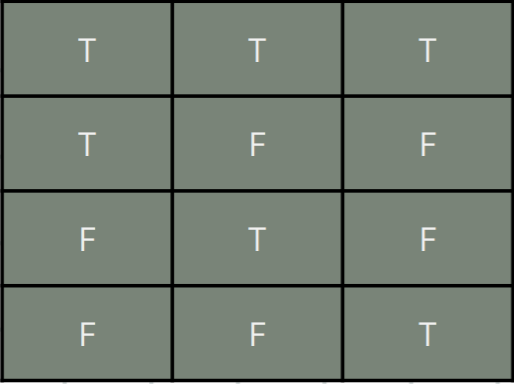
Biconditional