signal processing

equation to test for an energy signal if the signal is f(t), and thus its power is f(t)²

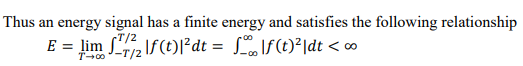
equation to test for a power signal,

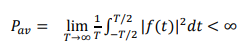
what is the power of an energy signal

zero, because it is finite energy divided by infinite time

what is the energy of a power signal

infinite, because the energy continues for infinite time (for there to be finite power) so there is infinite energy

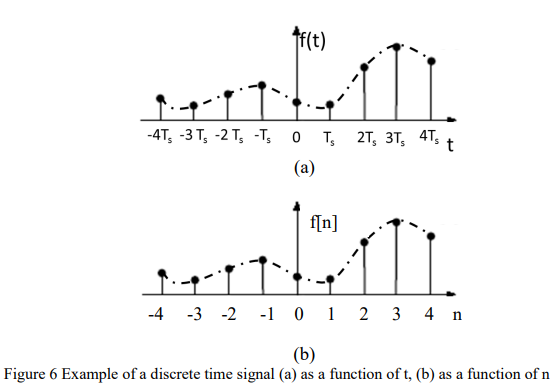
what is the difference between a continuous and a discrete time signal?

a continous signal has values at all times, like an analogue radio signal, or force on a wheel, etc, a discrete time signal has values only at discrete instants in time, nTs, where n is an integer and Ts is the time interval between the time samples

different ways for drawing a discrete time signal?

it can either be plotten as a function of Ts on the x axis, (a) or as a function of n on the x axis (b)

periodic time signal definition

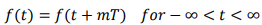
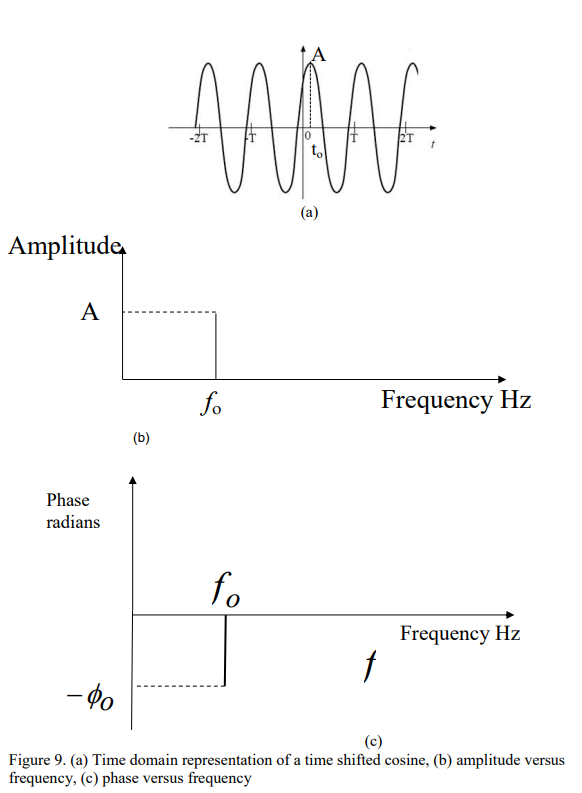
how to represent phase shift

f(t)=Acos(ω_ot + ϕ_o )

where ϕ_o = t_o*ω_o

what is the dB scale?

The dB scale is 10log_10(p2/p1) where p is power either in W (dBW) or mW (dBm)

what is the difference between dBW and dBm?

dBW or dBm are a measure of power into a 50  impedance when p1 is either 1 W, or 1mW, respectively.

how would you integrate cos(wt)²

us the trig identity that cos(wt)²=1/2[1+cos(2wt)]

the integrate that to get

when integrating to check if its an energy or power signal, how do you decide the limits?

they have to be over the time period T, which will tend to infinity, but you must check the limits for t given, and any other limits for constant given, as integrating between -infinity and + infinity will give different results than between 0 and infinity

what rule should you use when the energy signal has infinity on demon and num, or has zero on both denom and num?

use L’Hopitals rule, differentiate the top and bottom of the fraction with respect to T

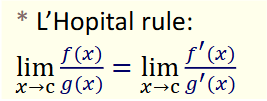
equation for P av of a sinusoid in terms of peak to peak voltage

V peak = V peak to peak/2, R=50

P av = V peak² / 2R

how to calculate dBW

dBW = 10 log10(P in watts/1)

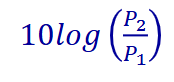
how to calculate dBm

dBW = 10 log10(P in mW/1)

how to convert from dBW to dBm

dBm=dBW+30

what is the synthesis equation for spectrum analysis

The synthesis equation for spectrum analysis decomposes a signal into its constituent frequencies by representing it as a sum of sinusoids, typically using Fourier series or Fourier transforms.

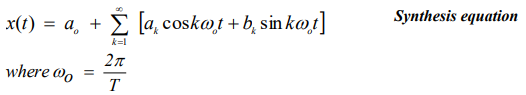
how to draw a SSS (single sided spectrum)

make sure to convert your equation into a form of Acos(n(2*pi*f)t+phi), if its a sin then do the phi - pi/2. Then use the A for the amplitude at the frequency given, if there are multiple frequencies in the signal then draw a line at each frequency at each amplitude. Do the same for the phase shift.

analysis equations for Spectrum analysis of a periodic continuous-time signal

when can you use fourier series?

for Spectrum analysis of a periodic continuous-time signal

euler identity general form

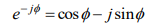
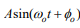
euler identity of Asin(w_o*t+phi_o)

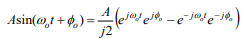
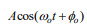
euler identity of Acos(w_o*t+phi_o)

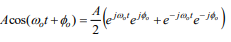
alternative Fourier series form (using Euler’s) DSS

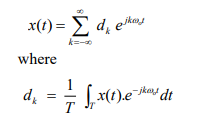
how to find dk for alternative fourier series (Eulers) DSS

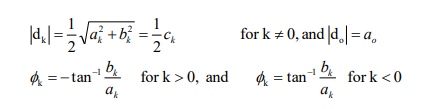
what is the single sided spectrum representation of the fourier series

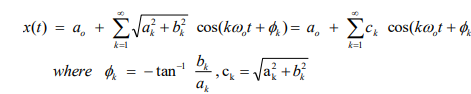
How can you use parseval’s theorem to find the average power of a signal from its Fourier series coefficients?

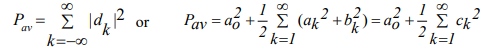
what is Parsevals theorem

the equation to find average power of a signal

difference between SSS and DSS?

positive and negative frequencies and complex coefficients which exhibit even symmetry in magnitude and odd symmetry in phase

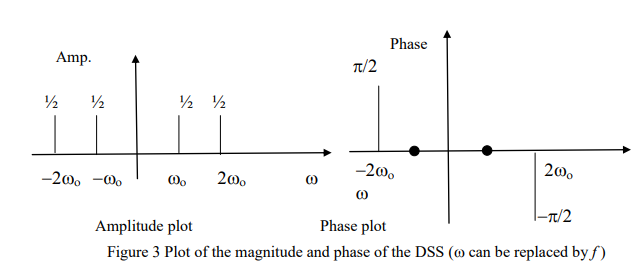
what are the rules to convert from SSS to DSS?

half the magnitude and reflect on y axis for amplitude

same magnitude and reflect on y and x axis for phase shift

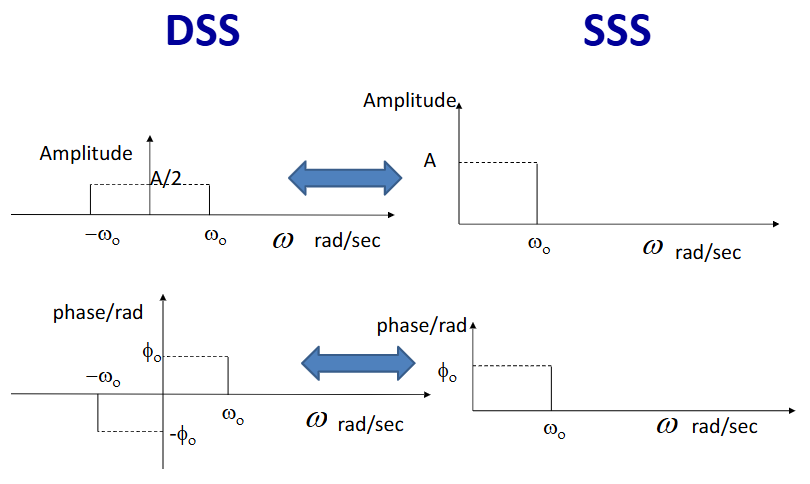
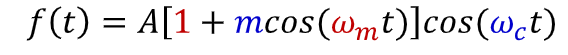
how would you sketch SSS of this signal?

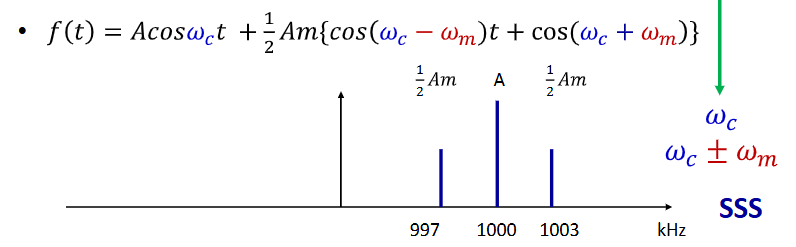
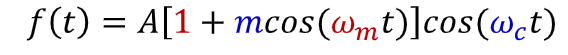
how would you sketch DSS of this signal?

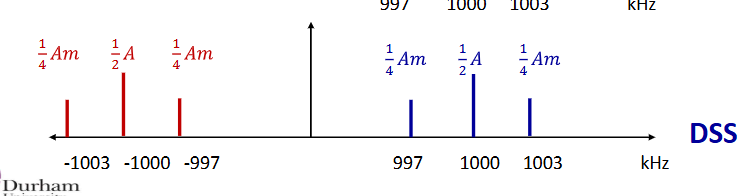
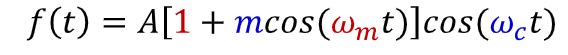
what type of signal is this?

Double sideband transmitted carrier

how to find the magnitude of dk (|d_k|)

½ sqrt(ak² + bk²), but for k=0, d_0=a_0

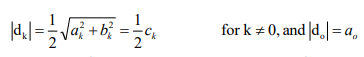
how to find the angle of d_k for k>0

- tan^-1 (bk/ak)

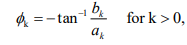
how to find the angle of d_k for k<0

tan^-1(bk/ak)

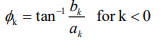
how to get dk from ak and bk (shortcut using imaginary)

for k>0, d_k = 1/2(a_k-jb_k)

for k<0, d_k = 1/2(a_k+b_k)

for k=0 d_k = a_0

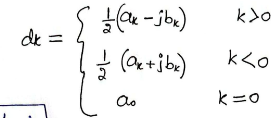
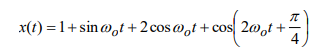
how would you find the compact coefficients for this signal?

a_0=d_0=1

a1=2, b1=1, put into equation d_k=1/2(a_k-j*b_k)

for d_2, use trig identity to get rid of the +pi/4, so you get cos(2wt)*cos(pi/4) - sin(2wt)*sin(pi/4), then use these to get a2 and b2, put that into same equation as before.

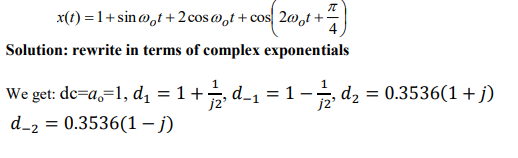
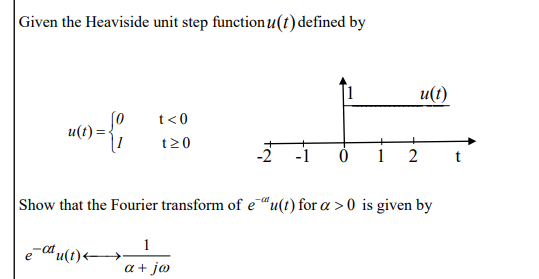
what are the steps to solving this question?

1) use u(t) to define the period over which you’re going to integrate for the fourier transform

2) since its 0 when t<0, go between 0 and inifnity

3) integrate over the period given

4) define the definite integral

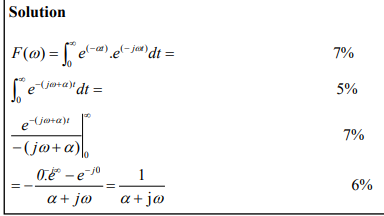
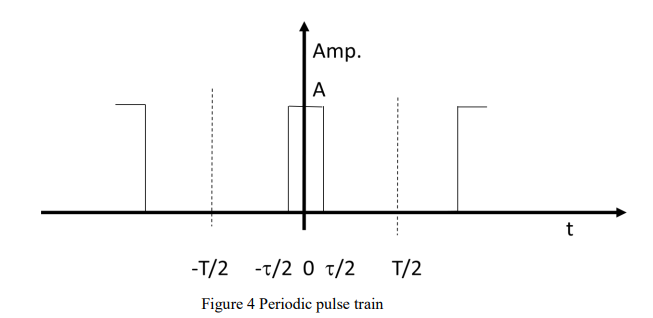
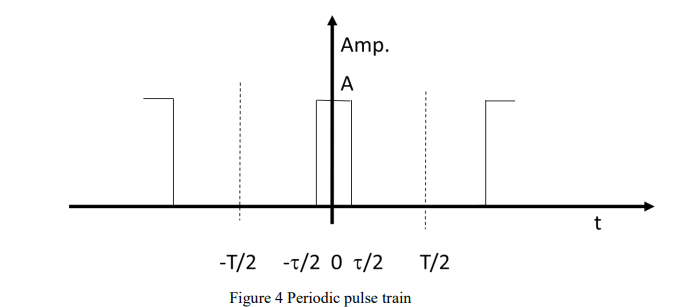
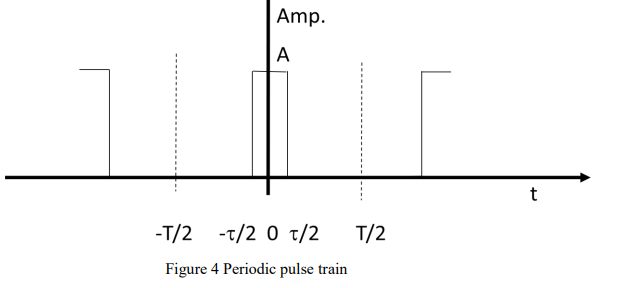
what is the function of the periodic pulse train?

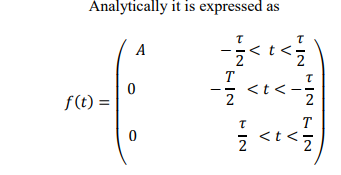
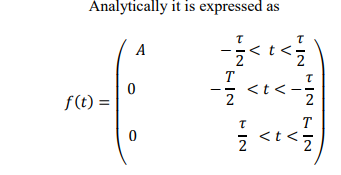
what would the amplitude time plot of this function look like and what is it called?

its a periodic pulse train. the pulse lasts for tau time, and repeats every T seconds.

if a function is even what does that mean for the Fourier series coefficients (ak and bk)?

b_k=0, so d_k=a_k/2

how do you normalise the values for an amplitude plot (or anything)

find the maximum value, then divide all values by the maximum value so that the maximum is 1.

what is the duty cycle of a pulse train?

a 5% duty cycle is the ratio of the width of the pulse to the period of the train, τ/T

equation for Fourier series coefficients of a periodic pulse train

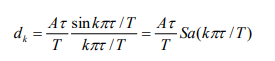
what does it mean if a waveform of a signal has even symmetry?

it means we can assume b_k=0, so d_k=1/2 a_k

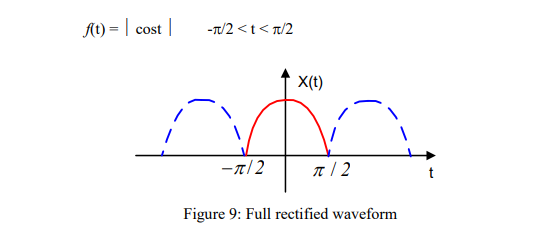
a_k fourier coefficient of a rectified wave

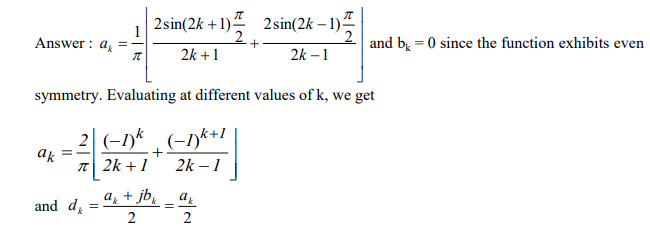
what are the 3 variables in a periodic pulse train?

T- the time period - defined the width between harmonics

tau - the pulse width - defines the zero crossings of the harmonics

duty cycle - defines the bandwidth

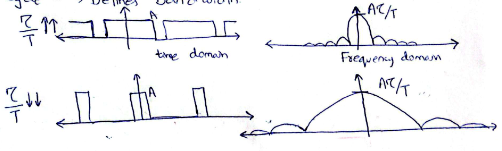
what would the impulse function delta(t) multiplied by the signal f(t) give?

it would give an impulse at t=0 of value of f(0)

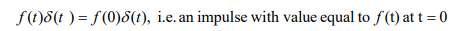
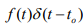
what would this give?

an impulse at time t_0 of value f(t_0)

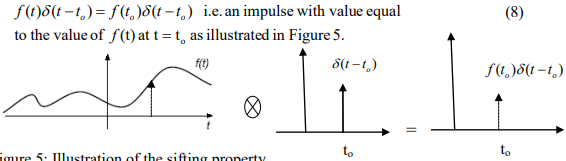
can you find the fourier transform of f(t)=1?

Replacing infinity in the result of the integral shows that it is not possible to use FT to evaluate f(t) directly. This is why the impulse function is useful because it overcomes the problem of not being able to use the FT

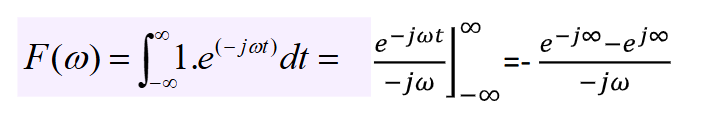
how to find the impulse response of a low pass filter

write out the equation for the filter in frequency domain

do the inverse Fourier transform of that filter

that is the impulse response

what is the inverse fourier transform of 1

2 * pi * delta durac function(t)

What are the advantages of digital implementation of signal processing?

1) Signals and Systems are Stored in Digital Computers and transmitted in Digital Form, so important to process digital signals instead of converting to analogue and then back again

2) DSP is stable and reliable in Contrast to Analogue Components which drift with Temperature, Humidity, Time, Etc

3) DSP can be used to process a number of signals simultaneously (TDM - time division multiplexing)

4) Accuracy can be precisely controlled in contrast to analogue Systems where Component Tolerances and Inaccuracies Are Not Precisely Known. ( assume compnent has 10% accuracy but not known, digital systems have precise number of bits)

5) More powerful DSP devices are becoming available at lower costs - so its more affordable

6) Digital filters offer the following advantages:
Can be made very close to ideal (sharp cut-offs, precise frequency behavior).

Can implement very low-frequency filters without physically large components.

Can be adaptive (change in real time), which is useful in applications like noise cancellation or communications.

Can have linear phase, meaning no distortion in signal timing—a feature hard to get in analog filters.

what are the advantages of digital filters?

• Can be made very close to ideal (sharp cut-offs, precise frequency behavior).

• Can implement very low-frequency filters without physically large components.

• Can be adaptive (change in real time), which is useful in applications like noise cancellation or communications.

• Can have linear phase, meaning no distortion in signal timing—a feature hard to get in analog filters.e.

what is a time invariant system?

Time invariance means that the system response remains unchanged with the time of the excitation so
if x(t) gives y(t) then x(t-to) gives y(t-to)

What is the impulse response of a system?

It is the output of a linear time-invariant (LTI) system when the input is an impulse function δ(t); denoted h(t)

What is the unit step response of a system?

It is the output of an LTI system when the input is a unit step function u(t) denoted s(t)

How are the impulse response h(t) and step response s(t) related?

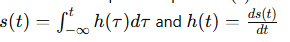
Why is the impulse response important?

It fully characterizes an LTI system in the time domain and allows output to be computed by convolution.

Give two advantages of digital over analog signal processing

1) Digital systems are more stable and not affected by temperature/humidity; (2) Precision is controllable via bit depth.

Why is DSP better for low-frequency filters?

Digital filters can implement very low-frequency cutoffs cheaply, whereas analog filters would require impractically large components.

What is one key benefit of digital filters regarding phase?

They can be designed to have linear phase, preserving signal shape (no phase distortion).

What makes digital filters adaptive?

They can change in real time using microprocessors, allowing dynamic adjustments to the signal or environment. like in noise cancellation