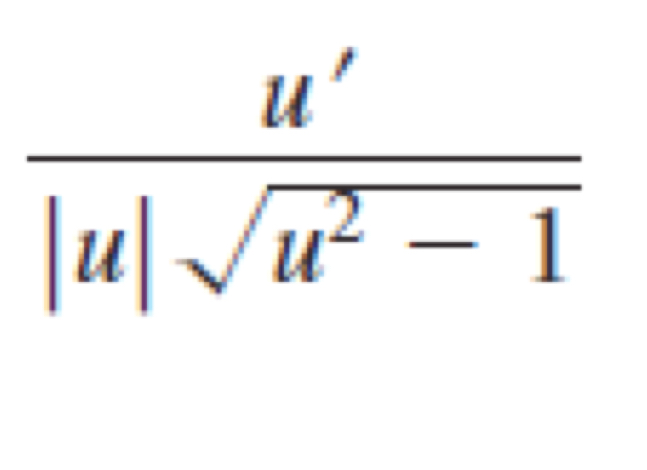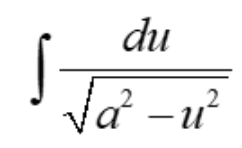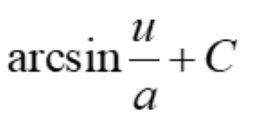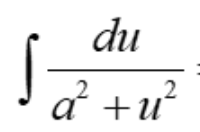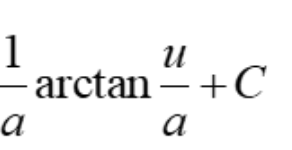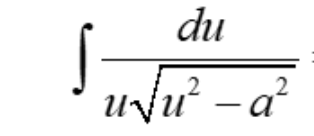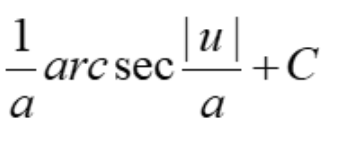Calc Unit 2 - Derivatives

Derivatives, rates of change, power rule, chain rule, etc.

Average velocity

(Speed 2 - speed 1)/(x2 - x1)

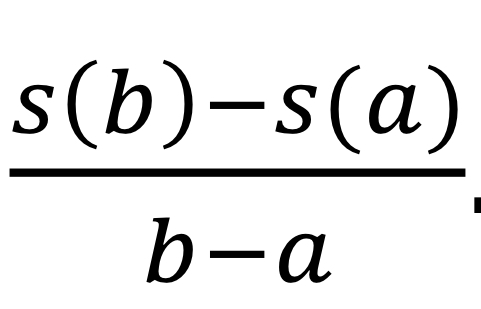
Limit definition of derivative

The limit as h approaches 0 of f(x+h) - f(x), all over h

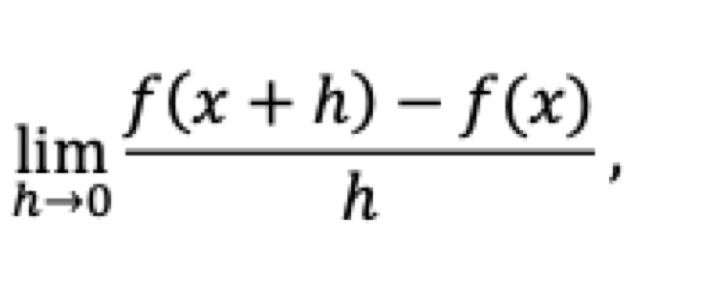
Limit definition of the derivative of a function f at the point (c, f(c ))

The limit as h approaches 0 of f(c+h) - f(c ), all over h

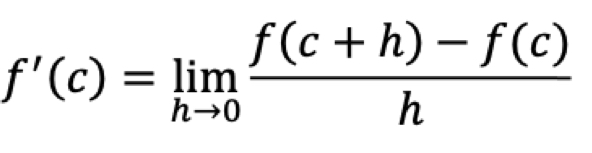
Alternative definition of the derivative of f at point c

Limit as x approaches c of f(x) - f(c ), all over (x-c)

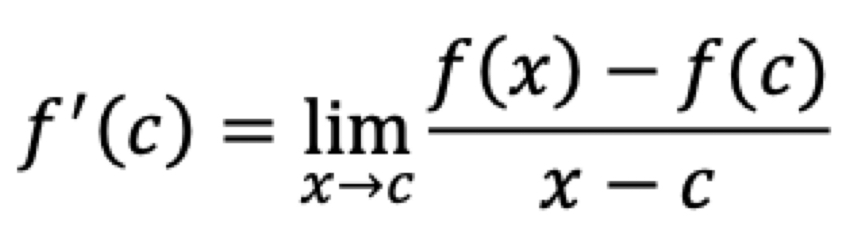
When is f(x) differentiable at x=c?

Limit as x approaches c from the left of f(x) - f(c ), all over (x-c) is equal to limit as x approaches c from the right of f(x) - f(c ), all over (x-c)

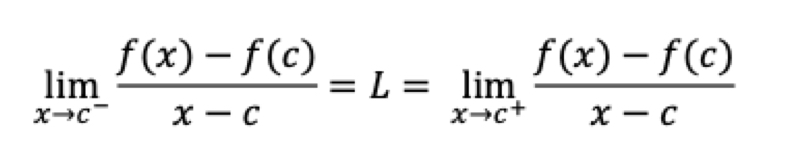
Derivative of sin x

Cos x

Derivative of cos x

-sin x

Derivative of sec x

sec x tan x

Derivative of csc x

-csc x cot x

Derivative of tan x

Sec²x

Derivative of cot x

-csc²x

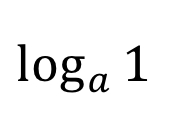
0

e =

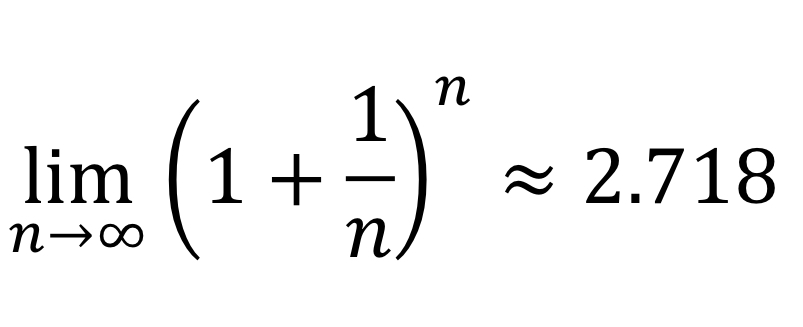
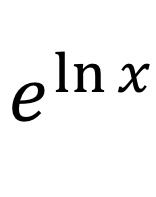
x

Derivatives of inverse functions are

Reciprocals

If g(x) is the inverse of f(x), then g’(x) =

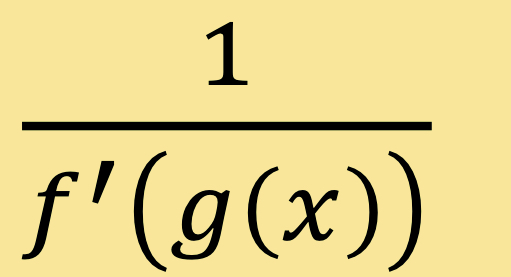
Derivative of ln u

U prime over u

Derivative of a^x

a^x * ln a

Derivative of a^u

u’ * a^u * ln a

Derivative of log_ax

1/(x ln a)

Derivative of log_au

u’/(u ln a)

Derivative of arcsin u

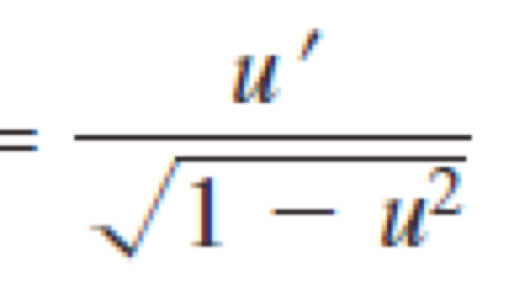
Derivative of arctan u

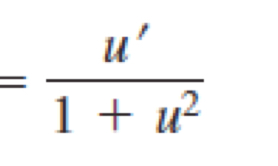
Derivative of arcsec u