Statistika - pojmy ke zkoušce

náhodný pokus

náhodný pokus

realizace určitého systému podmínek, které vedou k nějakému předem neznámému výsledku

cokoli, co uděláme a nemáme ambice to počítat

náhodný jev

to, v co vyústí náhodný pokus

(př. narození dítěte a zjištění, zda je to chlapec nebo dívka)

neslučitelné jevy

(disjunktní)

jevy, které nemohou nastat současně

(všechny elementární jevy)

pravděpodobnost

fce, která náhodným jevům připisuje čísla z intervalu [0;1]

klasická pravděpodobnost

využívá se tam, kde náhodný pokus vede ke konečnému množství výsledků, z nichž jsou všechny stejně možné

(Pω1=Pω2=Pω3=Pω4=…Pωn=1/n)

P(A) = všechny příznivé výsledky/všechny možné výsledky

geometrická pravděpodobnost

pokud elementární jevy nastávají se stejnou pravděpodobností, ale je jich nekonečně mnoho

obě množiny, jejichž prvky srovnáváme, si představíme jako geometrické útvary => stanovujeme jejich míru (míra = délka, obsah, objem…)

P(A) = míra (A)/míra (Ω)

náhodná veličina

fce, připisující každému myslitelnému výsledku náhodného pokusu nějaké číslo

spojení mezi skutečností a čísly

pokud s náhodnou veličinou provedeme jakoukoli matematickou operaci, výsledkem je opět náhodná veličina

př. náhodná veličina výška a váha => náhodná veličina BMI

rozdělení pravděpodobnosti

stejné jako pravděpodobnost (mat. fce), ale její definiční obor množiny čísel, ne množiny elementárních jevů

př. Px ({1, 2, 3})=0,5

(jaká je pravděpodobnost …?)

př. Px ([140;150])=? => Jaká je pravděpodobnost, že je dítě vysoké od 140 cm do 150 cm?

distribuční funkce

př. Px((-∞;150])=? => Jaká je pravděpodobnost, že bude dítě menší než 150 cm?

Px ((-∞; x]) = Fx = distribuční fce

FX(x) = jaká je pravděpodobnost, že se náhodná veličina X bude realizovat s hodnotou menší nebo rovnou libovolně zvolenému reálnému číslu x

((FX(x) = F, dolní index velké X, v závorce malé x))

vlastnosti distribuční fce

• není klesající => je rostoucí

• y nastoupá na 1

• na začátku je vždy 0 (nemusí být na x, ale na y je vždy)

spojitá náhodná veličina

má hladký průběh bez skoků

př. výška - může být 170,000, ale i 170,001, 170,0011 atd.

diskrétní náhodná veličina

graf vypadá jako schodiště

v některých bodech neroste a je konstantní - př. hod šestistěnnou kostkou => můžu hodit jen 1 nebo 2 nebo 3 atd. => nemůžu hodit 1,5 => v téhle hodnotě je pravděpodobnost 0

střední hodnota

E(X) = jakou hodnotu v průměru má realizace náhodné veličiny X

(může být + i -)

u diskrétních náhodných veličin se dá jednoduše spočítat - vynásobíme všechny hodnoty jejich pravděpodobnostmi a sečteme je - př. pohlaví => žena = 1 a muž = 2, obě mají pravděpodobnost 0,5 => 1×0,5 + 2×0,5 = 1,5

operace:
E(X + a) = E(X) + a
E(bX) = bE(X)
E(a + bX) = a + bE(X)
E(aX + bY + c) = aE(X) + bE(Y) + c

rozptyl (variance)

VAR(X) = jak jsou realizace rozmanité okolo střední hodnoty (jestli jsou těsně kolem toho nebo hooodně rozprostřené do stran)

(od 0 do +∞ => kladná čísla)

vysoký rozptyl => rozmanité hodnoty
nízký rozptyl => hodnoty těsněji u sebe

operace:
VAR(X + a) = VAR(X)
VAR(bX) = b²VAR(X)
VAR(a + bX) = b²VAR(X)

√VAR(X) = směrodatná odchylka

směrodatná odchylka

odmocnina z rozptylu (√VAR(X))

kovariance

COV(X, Y) = jak kolísání jedné náhodné veličiny (X) ovlivňuje kolísání druhé náhodné veličiny (Y)

statistický vztah, mění se pravděpodobnost jedné veličiny podle té druhé

COV (X, Y) = + => roste X, roste Y => kladný vztah
COV (X, Y) = - => roste X, klesá Y => záporný vztah
(( roste X, roste Y => vysoké hodnoty X vedou ke zvýšení pravděpodobnosti vysokých hodnot Y)
(př. inteligence a vzdělání => kladná kovariance)

korelační koeficient

pokud COV (X, Y) vydělíme směrodatnými odchylkami obou náhodných veličin => korelační koeficient (COR (X, Y))

hodnoty od -1 do +1

nezávislost náhodných veličin

hodnota jedné náhodné veličiny nesouvisí s hodnotou druhé náhodné veličiny => COV = 0

NULOVÁ COV NEZNAMENÁ NEZÁVISLOST! (je nelineární; př. rychlost řeči vyučujícího a objem odnesených informací => není to lineární => nulová COV)

pro nezávislé veličiny platí:
VAR(X + Y) = VAR(X) + VAR(Y)
E(XY ) = E(X)E(Y )

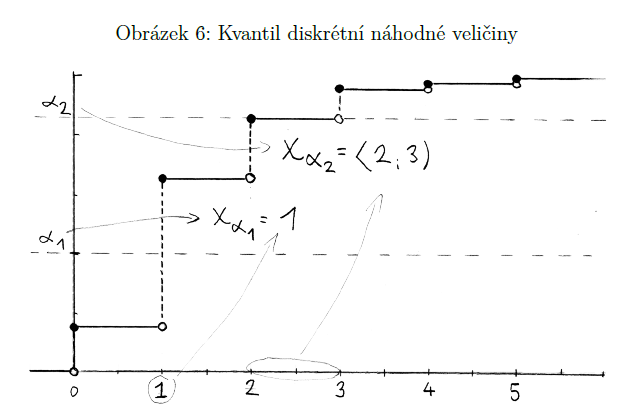
kvantil náhodné veličiny (alfa-kvantil)

opak distribuční fce

“Jakou hodnotu x bychom museli zvolit, aby v ní fční hodnota distribuční fce dosahovala nějaké námi stanovené pravděpodobnosti α” => α-kvantil (xα)

dáme pravděpodobnost => dá nám číslo (α=P)

stanovím α => xα = takové číslo, pro které platí, že se náhodná veličina realizuje v něm nebo v libovolné menší hodnotě s pravděpodobností α

př. jaké IQ musím mít, abych měla víc než 99 %

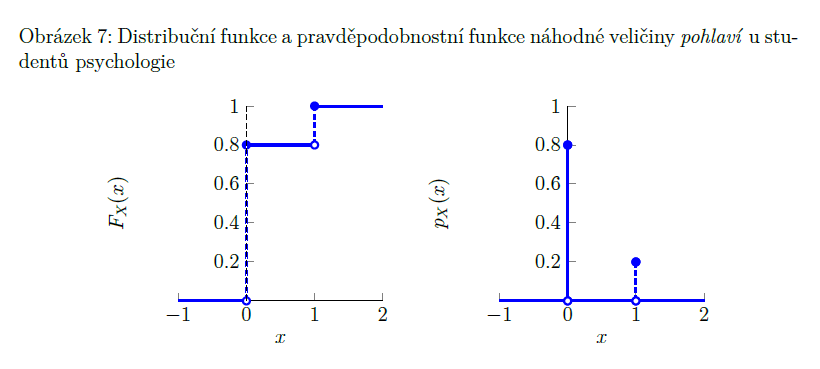
pravděpodobnostní funkce

pravděpodobnost toho, že náhodná veličina X se realizuje v hodnotě x = p_X(x) (p_X(x) = P (X=x))

pro diskrétní náhodné veličiny

přesně odpovídá výšce jednotlivých schodů distribuční fce diskrétní náhodné veličiny

pro spojité náhodné veličiny nemá smysl => P, že bude přesně takovéhle x, je nulová

hustota pravděpodobnosti

vlastnosti: je to kopec, který jde od 0 do 1 a pak znovu do 0; obsah tvaru je 1 (100 %)

značí se: f_x(x) ((první x je dolní index))

alternativní rozdělení

X ∼ Alt(p) => tato náhodná veličina má pouze 2 možné výsledky (0 nebo 1)
p = pravděpodobnost, že bude výsledek 1 (př. p=0,3 => 1 se objevuje s 30% pravděpodobností)

diskrétní rozdělení

E(X) = p
VAR(X) = p*(1-p)

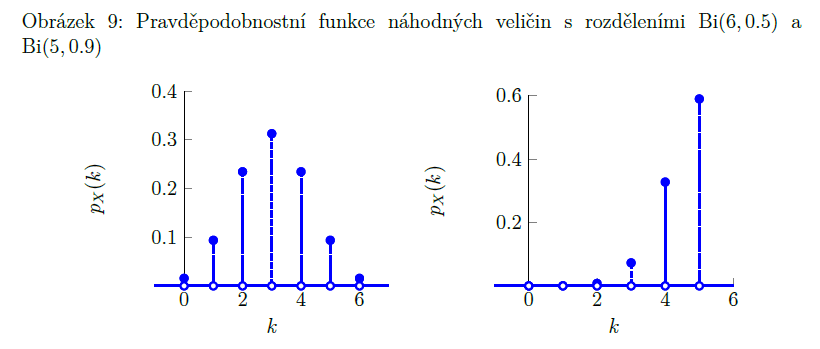
binomické rozdělení

X ∼ Bi(n, p)

součet n náhodných veličin, které mají každá pravděpodobnost p (že dostaneme 1 a ne 0) ((každá má alternativní rozdělení se stejnou p)
jednotlivé náhodné veličiny musí být NEZÁVISLÉ!

př. 10x hodím kostkou, jaká je P, že přesně 3x padne šestka?

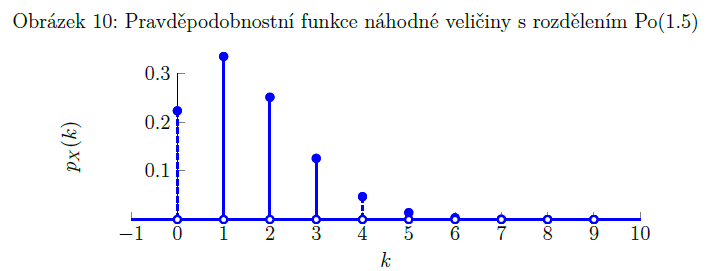
Poissonovo rozdělení

binomické rozdělení, kdy p je mega málo (blíží se nule) a n je mega moc (blíží se nekonečnu)

(krajní případ binomického rozdělení)

np = λ

má jediný parametr => λ => Po(λ)

u binomického rozdělení je n omezené, u Poissonova rozdělení je n neomezené

př. počet hvězd, které uvidíme, když se podíváme dalekohledem (hvězd je nekonečno, ale pravděpodobnost, že uvidíme zrovna tu jednu z nich, je zanedbatelná)

rovnoměrné rozdělení

X ∼ Ro (a, b) nebo (U (a, b))

a, b = parametry => a < b

př. délka čekání na tramvaj, když v náhodný čas přijdeme na zastávku, kde v pravidelných intervalech jezdí tramvaj

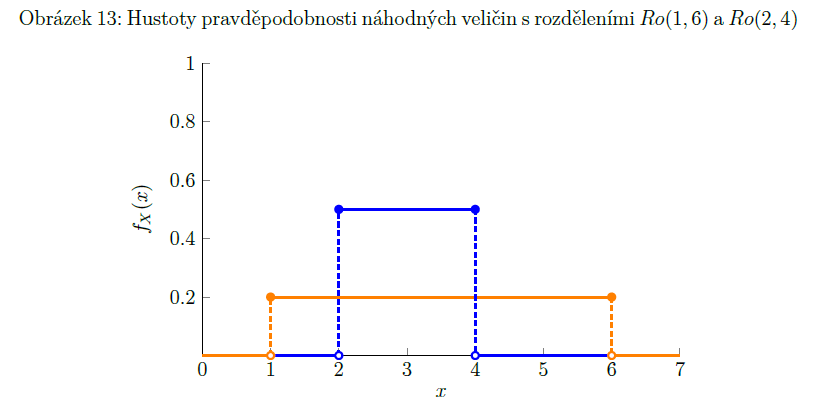
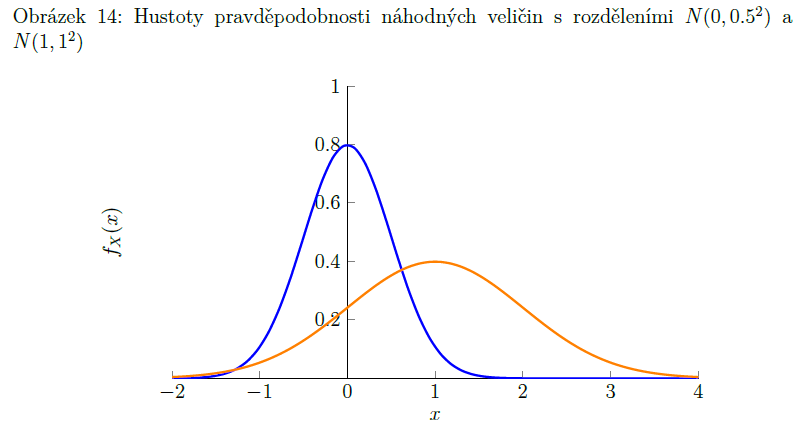
normální rozdělení

(Gaussovo rozdělení)

X ∼ N(μ, σ²)

vzniká tehdy, když sledovaná náhodná veličina představuje součet velkého množství nezávislých náhodných veličin s podobně velkými rozptyly

v přírodě velmi časté - př. tělesná výška lidí

má dva parametry: μ (střední hodnota) a σ² (rozptyl)

vlastnosti:
1. součet dvou náhodných veličin s normálním rozdělením vytvoří náhodnou veličinu s normálním rozdělením
2. pokud k náhodné veličině s normálním rozdělením něco přičteme/odečteme/vynásobíme/vydělíme ji (nenulovým číslem) => vzniklá náhodná veličina má opět normální rozdělení

(neexistuje nenormální)

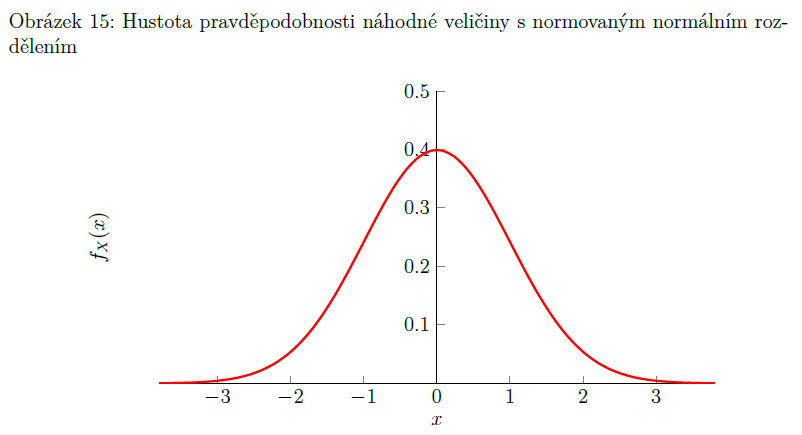
normované normální rozdělení

speciální případ normálního rozdělení - střední hodnota je 0 a rozptyl je 1

X ∼ N (0, 1)

hustota pravděpodobnosti norm. normál. rozdělení je symetrická okolo 0 => většina toho se organizuje od -3 do 3

převod normálního rozdělení na normované normální rozdělení:
X∼ N(μ, σ²) => Z ∼ N(0, 1)
Z = (X − μ)/σ

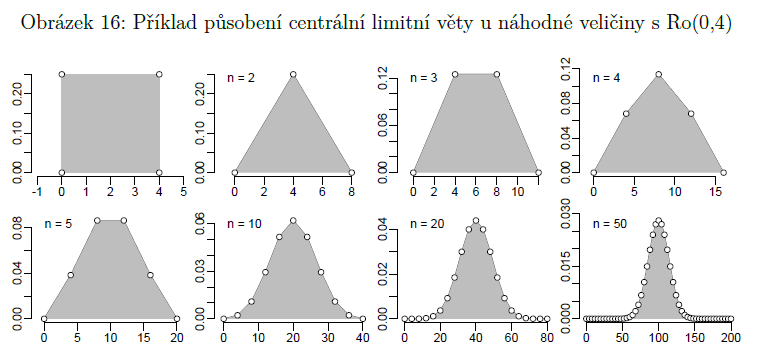
centrální limitní teorém

součet velkého množství nezávislých náhodných veličin s podobnými rozptyly bude čím dál víc připomínat normální rozdělení, čím víc jich bude

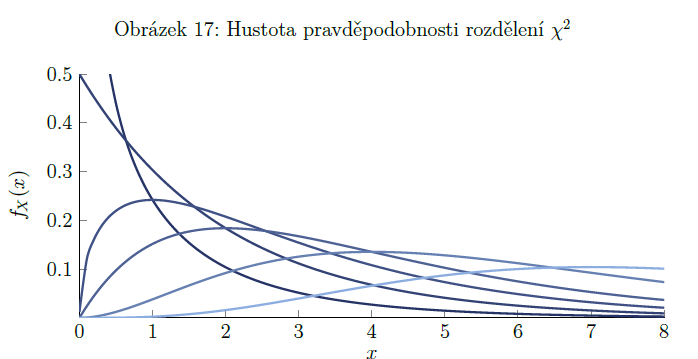
rozdělení chí kvadrát

pokud náhodnou veličinu s normovaným normálním rozdělením umocníme na druhou, získáme náhodnou veličinu Z², která má rozdělení chí kvadrát = X² (psáno chí, dolní index 1 a to celé na druhou) => spodní index označuje stupně volnosti = parametr rozdělení

př. 4 nezávislé veličiny ∼ N(0, 1) => součet jejich druhých mocnin bude mít rozdělení chí kvadrát se čtyřmi stupni volnosti

využití při tvorbě konfidenčních intervalů

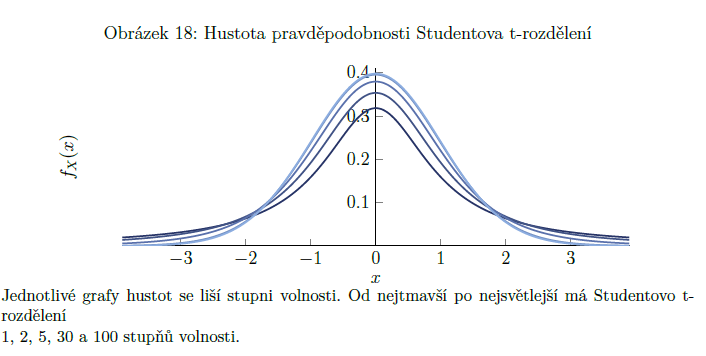
Studentovo t-rozdělení

potřebujeme: náhodnou veličinu Z₀ s normovaným normálním rozdělením + na ní nezávislou náhodnou veličinu “suma Z_i na druhou”, která má rozdělení chí kvadrát s n stupni volnosti => naše veličina se studentovým t-rozdělením bude míst stejně stupňů volnosti jako použitá vel. s rozdělením chí kvadrát

graf hustoty pravděpodobnosti připomíná normované normální rozdělení s těžšími chvosty (viz obrázek) => můžeme využít stejných vlastností jako u normovaného normálního rozdělení, jež vyplývají z jeho symetrie kolem nuly. S rostoucím počtem stupňů volnosti si jsou obě rozdělení podobnější, při n jdoucím k nekonečnu se stávají identickými

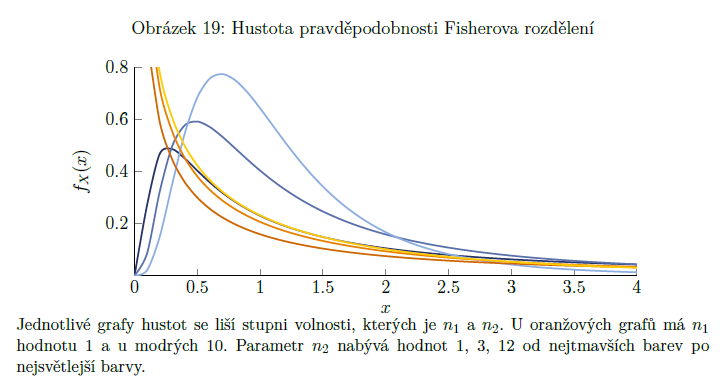
Fisherovo F rozdělení

získáme ho pomocí 2 nezávislých náhodných veličin (označíme je X1 a X2), které mají rozdělení chí kvadrát s n1 a n2 stupni volnosti => vzniklá náhodná veličina má Fisherovo rozdělení s n1 a n2 stupni volnosti (zapisujeme F ∼ Fn1,n2)

dva parametry: stupně volnosti veličiny v čitateli a stupně volnosti veličiny ve jmenovateli

pokud umocníme na druhou náhodnou veličinu s rozdělením tn, dostaneme náhodnou veličinu s rozdělením F1,n

absolutní četnost

počet prvků v úrovních statistických znaků

př. kolik je v souboru mužů (muž = úroveň statistického znaku pohlaví)

celé nezáporné číslo

značka: fj (j=označení dané kategorie, podsouboru)

relativní četnost

poměr, počet procent zastoupení

značka: pj

pj=fj/n (př. 3 lidi z 10 mají v souboru modré oči (3 = absolutní četnost) => 3/10 => relativní četnost = 0,3)

kumulativní četnost

kolik prvků má stejnou nebo menší hodnotu

př. kolik dětí má 5 sourozenců a méně

(je to jako distribuční fce)

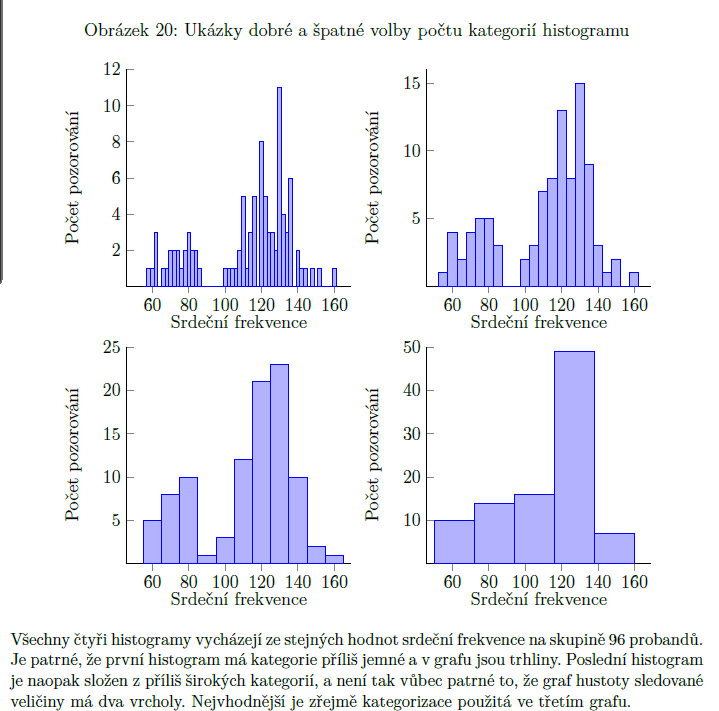
histogram

grafické znázornění četností

interval z jedné strany uzavřený, z druhé otevřený => záleží na nás, zda z leva nebo z prava; je na nás, kolik si dáme kategorií a jak si nastavíme krajní hodnoty

pomáhá nám pozorovat přibližný tvar grafu hustoty pravděpodobnosti náhodné veličiny, která se ukazuje jako kvantitativní znak

odlehlá pozorování

významně svou hodnotou vybočuje

“outliers”

někdy je možné je vyřadit (př. zaměřuji se na studenty 20-26 let, ale dotazník mi vyplnili i 2 lidé mimo tuto kategorii X nemůžu je vyhodit, i když se mi nelíbí) => použiji robustní statistiku

aritmetický průměr

míra polohy

součet všech hodnot vydělený jejich počtem

ne vždy to má smysl (např. u nominálních hodnot - př. pohlaví)

využití jen u kvantitativních statistických znaků (když to budu dělat třeba z pořadí, musím si uvědomit, že tím vyjádřím jen průměrné pořadí a nic jiného)

vážený průměr

každá jednotka má váhu (některé prvky souboru jsou důležitější než jiné => mají jiné váhy => musím to započítat do průměru => vážený průměr)

pracujeme s hodnotami (x1, x2…) a jejich váhami (w1, w2…)

výpočet: suma wi*xi/suma wi

kromě různých vah se taky využívá, pokud máme průměry více skupin, které nejsou stejně obsáhlé (př. v jedné skup. je 10 lidí a ve druhé 12) => výpočet: n1*průměr1 + n2*průměr2 + … nn*průměrn/součet všech n

useknutý průměr

robustní modifikace průměru

seřadím pozorování (od nejmenší po největší) a z obou stran useknu stejný počet pozorování (x %)

př. 0 0 1 1 1 1 2 2 2 3 3 4 5 8 9 13 18 29 300 => podtržené hodnoty useknu a spočítám průměr z toho zbytku (z obou stran jsme usekli 4 hodnoty, což je 20 %) => původní průměr = 20,5 X useknutý průměr (20 %) = 4

winsorizovaný průměr

robustní modifikace průměru

podobné jako useknutý průměr, ale ty krajní hodnoty nevymažu, ale udělám z nich hodnoty, co jsou na kraji useknutí (u useknutého průměru)

př. 0 0 1 1 1 1 2 2 2 3 3 4 5 8 9 13 18 29 300 => z podtržených částí se mi stane: 1 1 1 1 a 9 9 9 9 => původní průměr = 20,5 X winsorizovaný průměr (w 20 %ú = 4,4)

výběrový medián

střed; u lichých počtů pozorování je to číslo uprostřed, u sudých je to průměr dvou středních hodnot

jde to u ordinálních, pořadových dat (průměr ne)

je vysoce robustní (průměr ne)

dělí to na dva stejně velké soubory/poloviny (po 50 %) ((dá se to brát jako krajní případ useknutého průměru, kdy ponecháme jen 1 nebo dva prvky)

výběrový kvantil

umožňuje nám rozdělit soubor v nějakém poměru - př. 25:75

α = číslo od 0 do 1

výpočet kvantilu: n*α
- pokud je výsledek celé číslo => kvantil = (x_n*α + x_n*α₊₁)/2
- jinak zaokrouhlíme výsledek n*α nahoru => značíme [nα] => kvantil bude xα = x_[nα_]

př. 0 0 1 1 1 | 1 2 2 2 3 3 4 5 8 8 9 13 18 29 300
n = 20; α = 25 % => n*α = 20×0,25 = 5 => udělám průměr 5. a 6. prvku

výběrový modus

jediná míra polohy, která se dá uplatnit i na kvalitativní data (tam se musí hodnoty dát do kategorií)

nejčastější hodnota v souboru

typy: unimodální (1 hodnota), bimodální (2 hodnoty- př. modus je 3 a 5), multimodální (3 a více hodnot - př. modus je 3, 5 a 12)

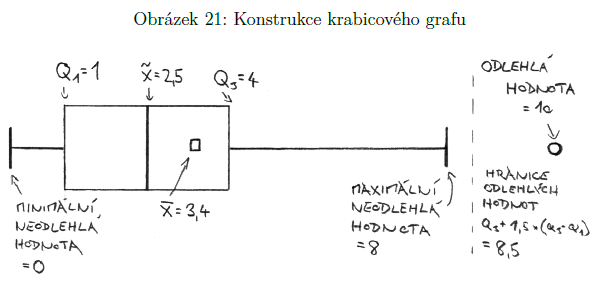
krabicový graf

vizualizace charakteristik míry polohy

části: krabička, jejíž hrany jsou na krajích kvartilů (Q1 a Q3) + čára znázorňující medián + vousy sahající k nejnižší a nejvyšší naměřené hodnotě, která ještě není odlehlé pozorování (odlehlá pozorování jsou 1,5 násobek mezikvartilového rozpětí => 1,5*(Q3-Q1))

výhody: opírá se o robustní ukazatele, ale zároveň ukazuje i odlehlá pozorování

variační rozpětí

R = Xmax-Xmin

míra variability

mezikvartilové rozpětí

IQR = Q3 - Q1 (Q3 = X_0,75; Q1 = X_0,25)

míra variability

průměrná absolutní odchylka

v průměru se lidé liší od průměru o …

značí se d (s čarou)

míra variability

sečteme absolutní hodnoty rozdílů jednotlivých měření od průměru a vydělíme je počtem

mediánová absolutní odchylka

robustnější než průměrná odchylka

značí se MAD

míra variability

MAD kolem průměru: sečteme absolutní hodnoty rozdílů jednotlivých měření od průměru a vybereme z toho medián

MAD kolem mediánu: sečteme absolutní hodnoty rozdílů jednotlivých měření od mediánu a vybereme z toho medián

výběrový rozptyl (variance)

míra variability

průměr součtu čtverců (součet čtverců = součet druhých mocnin rozdílů jednotlivých hodnot od průměru) (POZOR! - nedělí se SČ celkovým počtem, ale n-1)

vlastnosti:

• lze ho počítat jen na kvantitativních znacích; pokud sledovaný znak označuje pořadí, tak (podobně jako v případě průměru) rozptyl lze spočítat, avšak získaný údaj se bude vztahovat zase pouze k pořadí, ne k původní veličině, podle které byla měření seřazena.

• Rozptyl nikdy nemůže být záporný.

• Pokud je rozptyl roven nule, znamená to, že všechny naměřené hodnoty jsou přesně stejné (tedy rovné průměru).

• Rozptyl je velmi citlivý na odlehlá pozorování.

• Podobně jako jsme definovali useknutý a winsorizovaný průměr, můžeme definovat useknutý a winsorizovaný rozptyl, respektive směrodatnou odchylku. Získáme tak ukazatele s vyšší robustností.

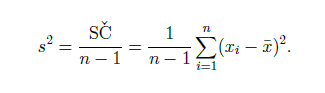
výběrová směrodatná odchylka

míra variability

odmocnina z výběrového rozptylu

je jednodušší na pochopení než výběrový rozptyl

((kdyby bylo s = 0, tak i průměr by byl 0 a všechny pozorování mají stejnou hodnotu))

je velmi citlivá na odlehlá pozorování

můžeme udělat useknutou a winsorizovanou smerodatnou odchylku => vyšší robustnost

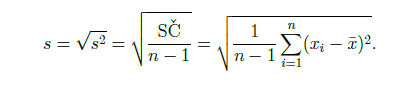
variační koeficient

používá se k porovnání velikosti variability u dvou různých znaků nebo ve dvou souborech

př. je výška variabilnější v souboru mužů nebo žen? => muži jsou obecně vyšší než ženy, takže rozdíl jejich směrodatných odchylek může být úměrný rozdílu v průměrné výšce

výpočet: směrodatná odchylka/průměr => vyjde nám relativní variabilita

udává, z kolika procent se směrodatná odchylka “vepisuje” do aritmetického průměru

nemá jednotky, vyjadřuje se v procentech

nelze ho počítat vždy => sledovaný statistický znak musí odpovídat množství něčeho => 0 musí být nulové množství atd. (=> nejde to u IQ, stupňů Celsia…)

mutabilita

zjišťuje variabilitu u KVALItativních znaků - př. barva očí => mají ji všichni v souboru stejnou nebo každý jinou?

pravděpodobnost toho, že když vylosuju 2, tak budou různé (2 jiné úrovně nominálního znaku) - př. pravděpodobnost toho, že když vylosuju dva lidi ze souboru, tak jeden bude mít každý jinou barvu očí

nabývá hodnoty od 0 do 1

n pozorování, k skupin - př. barvy očí - modrá = f1, hnědá = f2, zelená = f3, atd.

pokud je supin méně než počtů pozorování, mutabilita nikdy nedosáhne hodnoty 1 (max. hodnota bude pak (n(k-1))/(k(n-1))

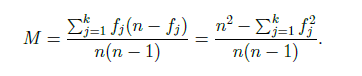
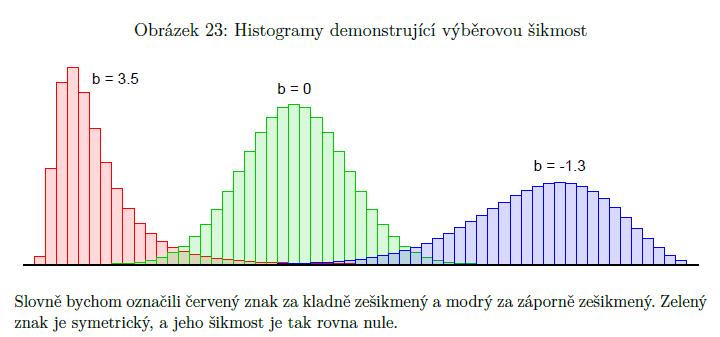
výběrová šikmost

pro lepší představu histogramu našich měření

ukazatel toho, do jaké míry je uspořádání nalezených hodnot symetrické kolem jejich aritmetického průměru (= míra asymetrie)

značí se b
b > 0 => častější realizace podprůměrných hodnot, protažený pravý chvost (vlevo jsou vysoké sloupce a směrem doprava jsou menší)
b < 0 => častější realizace nadprůměrných hodnot, protažený levý chvost (vlevo jsou malé sloupce a směrem doprava jsou velké)
b = 0 => symetrické

čím vyšší číslo, tím delší chvost (ocásek)

protějšek teoretické šikmosti (pomocí toho popisujeme rozdělení náhodné veličiny), symetrická rozdělení (normální, studentovo…) mají šikmost nulovou

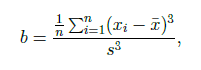
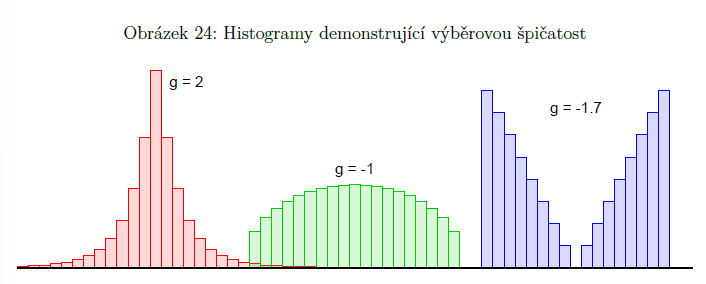
výběrová špičatost

jak moc jsou hodnoty namačkané ve středu (jak moc se hodnoty točí okolo průměru)

na rozdíl od šikmosti (která nás zajímá u nesymetrických rozdělení) nás špičatost zajímá u symetrických rozdělení

značí se g

ve vzorci se odečítá číslo 3, aby hodnotám, které pocházejí z normálního rozdělení náležela v průměru výběrová špičatost 0 (normální rozdělení by jinak mělo špičatost 3) => díky tomu špičatost značí, o kolik je tvar sledovaného znaku špičatější než normální rozdělení

g < 0 => málo špičaté, placatější než normální rozdělení
g > 0 => hodně špičaté, špičatější než normální rozdělení

pokud jsou hodnoty hodně k minimu a maximu než k průměru, bude špičatost hodně záporná

protějšek teoretické špičatosti, která analogickým způsobem popisuje tvar grafu hustoty pravděpodobnosti náhodné veličiny

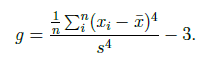
výběrová kovariance

míra závislosti

zobecnění rozptylu, který spolu 2 znaky sdílí
VAR (X) = COV (X,X)

s > 0 => vysoké hodnoty x souvisejí s vysokými hodnotami y (rostoucí x má tendenci v průměru k rostoucímu y)
s < 0 => vysoké hodnoty x se pojí spíše s nízkými hodnotami y (rostoucí x má tendenci v průměru ke klesajícímu y)
s = 0 => není lineární vztah (nedá se říct, že by rostoucí x souviselo s rostoucím nebo klesajícím y)

většinou se nepoužívá pro popis, ale jenom jako dílčí krok při výpočtech (má divné jednotky - př. body IQ krát centimetry)

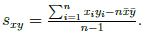
Pearsonův korelační koeficient

není v jednotkách

v intervalu od -1 do 1

značí se r (+ je symetrický => r_xy = r_yx)

těsnost vztahu podle r:
|r| < 0.1 zanedbatelný vztah
|r| < 0.3 slabý vztah
|r| < 0.5 středně silný vztah
|r| ≥ 0.5 silný vztah
r = 1 přímá úměra

r = 0 vztah mezi znaky není lineární

nezmění se, i když jeden ze znaků (x nebo y) vynásobíme, vydělíme, přičteme k němu něco

r_xy = r_{ax+b, y} (pokud budu násobit záporným číslem => změní se znaménko r (obrátí se, z kladného bude záporné a naopak)

není robustní!
popisuje to korelaci, ale ne kauzalitu
popisuje to v průměru
ideální pro data bez outlierů, metrická data…

standardizovaná kovariance => vydělení kovariance směrodatnými odchylkami obou znaků

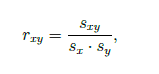
bodově-biseriální korelační koeficient

varianta Pearsonova korelačního koeficientu

stejný jako Pearson, když máme jednom sloupci pouze hodnoty 0 a 1 (nominál.)

pouze v intervalu od -1 do 1

značka: r_pb

popisuje pouze lineární vztahy

př. jedním znakem je pohlaví

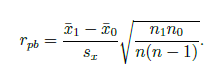
koeficient fí

varianta Pearsonova korelačního koeficientu

stejný jako Pearson, když oba sledované znaky nabývají pouze hodnot 0 nebo 1

značí se rϕ (fí)

zapisuje se to do tabulky 2×2 (čtyřpolní tabulka) - každá statistická jednotka může patřit do jedné ze 4 kategorií: 1-1, 1-0, 0-1, 0-0

př. je více leváků mezi muži nebo ženami?

ne vždy se pohybuje v intervalu od -1 do 1 - nedosáhneme do kraje, pokud nejsou stejné poměry na obou stranách (př. leváci : praváci ≠ muži : ženy => nemůže nám to vyjít (-)1)

Spearmanův korelační koeficient

dám hodnotám pořadí od největší po nejmenší (nebo naopak) v obou sloupcích => spočítám druhou mocninu rozdílů pořadí v hodnotě prvního a druhého znaku (d²) => hodím to do vzorce

X když jich má několik stejné pořadí (př. 1, 6, 7, 6, 5 => 5., 2.-3.=2,5., 1., 2.-3.=2,5., 4.) => nemůžu na to použít Spearmana => musím použít Pearsona

je vysoce robustní, o dost více než Pearsonův korelační koeficient (outlieři nejsou => je fuk, jestli mám poslední hodnotu 300 nebo 300 000)

dá se použít i na ordinální proměnné

můžeme ho spočítat i tehdy, když nemáme původní data, stačí nám vědět pořadí u obou znaků

dokáže popsat libovolný monotónní vztah (rostoucí/klesající), nejen ten lineární (na rozdíl od Pearsona) ((př. pokud by platilo, že y=x², tak by Spearman vyšel 1, ale Pearson by vyšel asi menší)

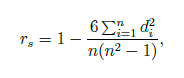
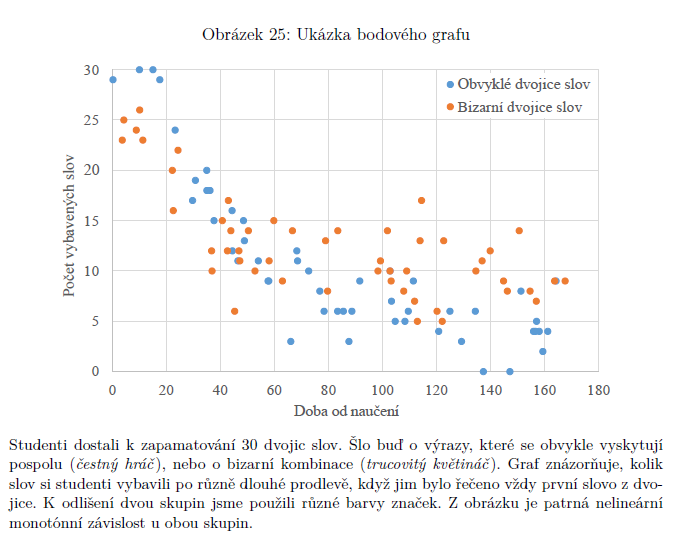
bodový graf

je lepší vidět celá data v grafu, než je zredukovat na jedno číslo (Spearman, Pearson)

některé vztahy nejdou ani Pearsonem ani Spearmanem, ale jsou vidět v grafu (nejsou lineární ani rostoucí nebo klesající, ale jsou třeba jako kopec (nejdřív nahoru, pak dolu)

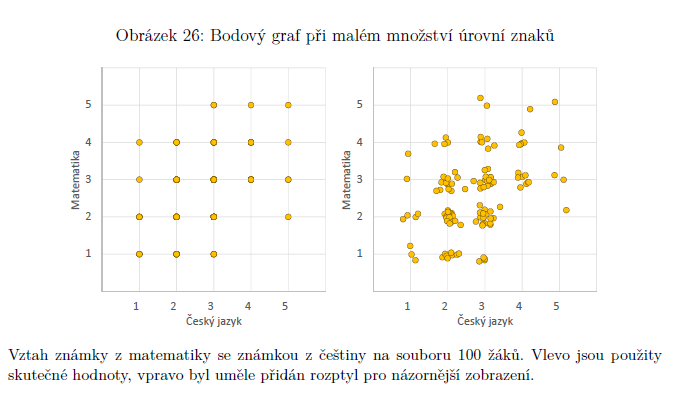
omezení: když oba sledované znaky nabývají jen malého počtu různých hodnot (př. souvislost známky z čj se známkou z matematiky) => vyřešíme to přičtením náhodných čísel, která nezmění interpretaci, ale pomůžou nám vyčíst to, co potřebujeme (obvykle jsou to čísla z normálního rozdělení se středem v nule a malým rozptylem)

vlastnosti bodových odhadů

estimátor je statistika (tedy náhodná veličina vytvořená z prvků náhodného výběru), která má tendenci se realizovat kolem skutečné hodnoty hledaného parametru

měřením získáme jednu realizaci náhodného výběru => získáme tím jednu realizaci našeho estimátoru => estimát (odhad)

u estimátoru požadujeme tyto vlastnosti:

• výpočet se musí opírat pouze o náhodný výběr (X1, X2, X3,…Xn)

• nevychýlenost/nestrannost = nepodhodnocuje, nenadhodnocuje => střední hodnota estimátoru = střední hodnota odhadovaného parametru (E(X s pruhem)=μ) (aritmetický průměr je nestranný; kde se v průměru realizuje aritmetický průměr)

• rozptyl estimátoru je nejmenší možný - motá se co nejmíň okolo té hodnoty (VAR(X s pruhem) => pokud je i nestranný = nejlepší nestranný odhad

• čím více pozorování (n), tím přesnější => konzistentní odhad (čím větší soubor, tím konzistentnější odhad, přesnější estimátor)

• nedá se vyrobit žádný estimátor, který by byl lepší (nejmenší rozptyl)

náhodný výběr

uspořádaná entice náhodných veličin, které mají indetické rozdělení pravděpodobnosti

• všechny náhodné veličiny jsou stejné (= mají stejné rozdělení pravděpodobnosti), liší se jen jmény, které jsme jim dali

  • podmínky identického rozdělení zajístíme tím, že všechna pozorování budeme provádět za stejných podmínek + zařídíme nezávislost (př. u pozorování aut - budeme je pozorovat s časovými odstupy, aby se řidiči nemohli ovlivnit)

• jsou vzájemně NEZÁVISLÉ!

nkrát realizujeme veličinu X s normálním rozdělením => realizujeme klony této veličiny, ntice

n naměřených hodnot (x1, x2, x3,…,xn) představuje jedinou realizaci náhodného výběru X

náhodná veličina nemá číslo, když se realizuje, realizuje se číselně

libovolná kombinace náhodných veličin je také náhodná veličina, tedy i náš průměr X (s pruhem) je náhodnou veličinou se svou distribuční funkcí, střední hodnotou, rozptylem atd.

Funkce, jejímž argumentem je náhodný výběr, se nazývá výběrová funkce neboli statistika.

př. malé x s pruhem = realizace náhodné veličiny X s pruhem

populační vs. výběrová variance

estimátor rozptylu = výběrový nebo populační rozptyl

máme k dispozici jen n prvků vybraných z větší populace => použijeme výběrový rozptyl => nestranný (E(S²) = σ²), širší rozptyl (ve jmenovateli je 1-n),

máme k dispozici všech N prvků (n=N) => použijeme populační rozptyl => přesnější, ale podhodnocuje (ve jmenovateli je n), je nejlepší možný (má nejmenší rozptyl)

obvykle dáváme přednost výběrovému rozptylu

(rozdělení výběrového rozptylu je modifikovaný chí kvadrát (stupně volnosti n-1))

populační vs. výběrová kovariance

stejné problémy jako u estimátoru rozptylu

nemá symetrickou hustotu pravděpodobnosti → nejsme schopni vytvořit jeden estimátor, který by splňoval všechny požadavky zároveň → máme dva estimátory

populační kovariance - není nestranná (je pouze asymptoticky nestranná) + je nejlepší možná (má nejmenší rozptyl, estimáty méně kolísají)

výběrová kovariance - je nestranná (E(S_xy) se rovná skutečné hodnotě s_xy), není nejlepší možná (VAR(S_xy) není ten nejmenší – více kolísá)

obvykle dáváme přednost výběrové kovarianci

jednostranný a dvoustranný konfidenční interval

jelikož náš bodový odhad nebude nikdy přesný (μ nikdy nebude přesně stejné jako x s pruhem (průměr))

=> je lepší prezentovat to v intervalech, aby to bylo přesnější

intervaly spolehlivosti = konfidenční intervaly

oboustranný konfidenční interval = dvojice statistik (dolní a horní), které když se realizují, tak s určitou spolehlivostí 1-α vytvoří interval, ve kterém se nachází námi hledaný parametr (př. μ)
(ta dolní statistika se realizuje s menší hodnotou, než je hodnota námi hledaného parametru, a horní statistika se realizuje s hodnotou větší, než je hodnota námi hledaného parametru)

je vždy stanoven s určitou spolehlivostí, kterou vyjádříme číslem mezi 0 a 1 (značí se 1-α, kde α značí nespolehlivost)

=> vytváříme interval, který v (1-α)*100 procentech případů (převedeme spolehlivost na procenta) pokrývá skutečnou hodnotu hledaného parametru

jednostranný interval je stejný jako oboustranný, jen nám říká pouze jednu hranici (druhá hranice není, je to buď od - nekonečna nebo do nekonečna) a při výpočtu se nepůlí α