PRECALC H: Flashcard sets 1-3

Solving Linear eqns & inequalities

Solving Linear eqns & inequalities

isolate the variable

Solving Quadratic eqns & inequalities

isolate zero

Solving polynomial eqns & inequalities

isolate zero

Solving Rational eqns & inequalities

multiply by the LCD

Solving absolute value eqns & inequalities

isolate absolute value

solving absolute value eqns

|a| =

a, if a>0

-a, if a<0

solving absolute value ineqalities

|f(x)| > c means…

f(x)>c

or

f(x)< -c

solving exponential equations

isolate the power

solving radical eqns

isolate the radical

solving log eqns

write as the log of one expression and then isolate the log

solve trig eqns

1) isolate the trig ratio

2) use zero product property

3) use a trig identity

to translate a graph up

add a #

to translate a graph down

subtract a #

to translate a graph right

subract a # “within”

to translate a graph left

add a # “within”

to vertically stretch a graph

multiply by a # c (c>1)

to vertically shrink a graph

multiply by a # c (0<c<1)

f(x) + k

translates a graph up k units

f(x) - k

translates a graph down k units

kf(x), where k>1

vertical stretch

kf(x), where 0<k<1

vertical shrink

f(x+h)

translates graph left h units

f(x-h)

translates graph right h units

to find x-intercepts

substitute 0 for y

to find y-intercept

substitute 0 for x

how to find inverse function

1) replace f(x) with y

2) switch x & y

3) solve for the new y

4) replace g(x) for the new y

properties of inverse function

1) symmetric with y=x

2) f(g(x)) = g(f(x)) = x

3) one-to-one function

4) Domain & Range are interchanged

f(kx), where k>1

horizontal shrink

f(kx), where 0<k<1

horizontal stretch

f(-x)

reflection across y-axis

-f(x)

reflection across x-axis

-f(-x)

reflection through origin

f(|x|)

reflection of QI & QIV through y-axis (lose QII & QIII)

|f(x)|

Reflection of QIII and QIV through x-axis (lose QI & QII)

1/f(|x|)

y → 0⁺ <-> y → +∞

y → 0^- <-> y → -∞

y = 0 <-> y is undefined

f(h-x)

= f(x+h) then replace xby - x (reflection of f(x+h) through y-axis)

|f(x)| defined as a piecewise function

f(x) for all x where f(x) ≥ 0

-f(x) for all x where f(x) < 0

even function

a function that is symmetric to itself through the y-axis; f(-x) = f(x)

odd function

a function that is symmetric to itself through the origin; -f(x) = f(x)

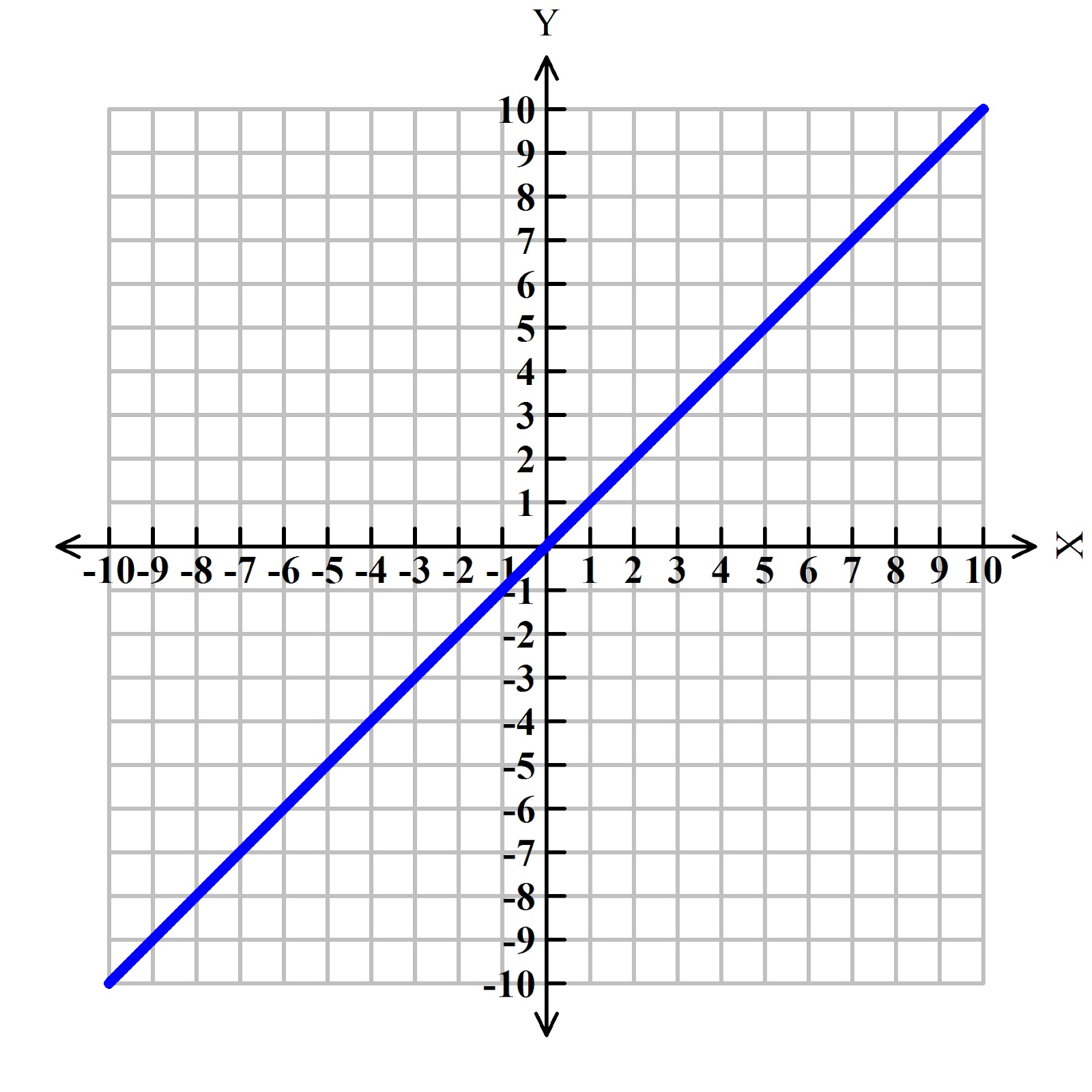
f(x) = x

linear family

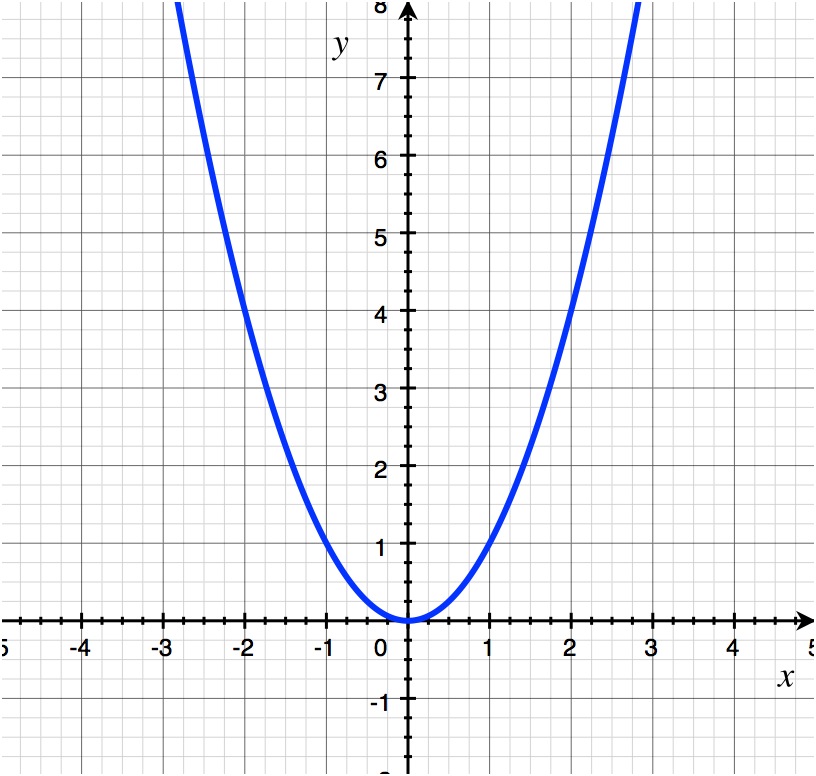
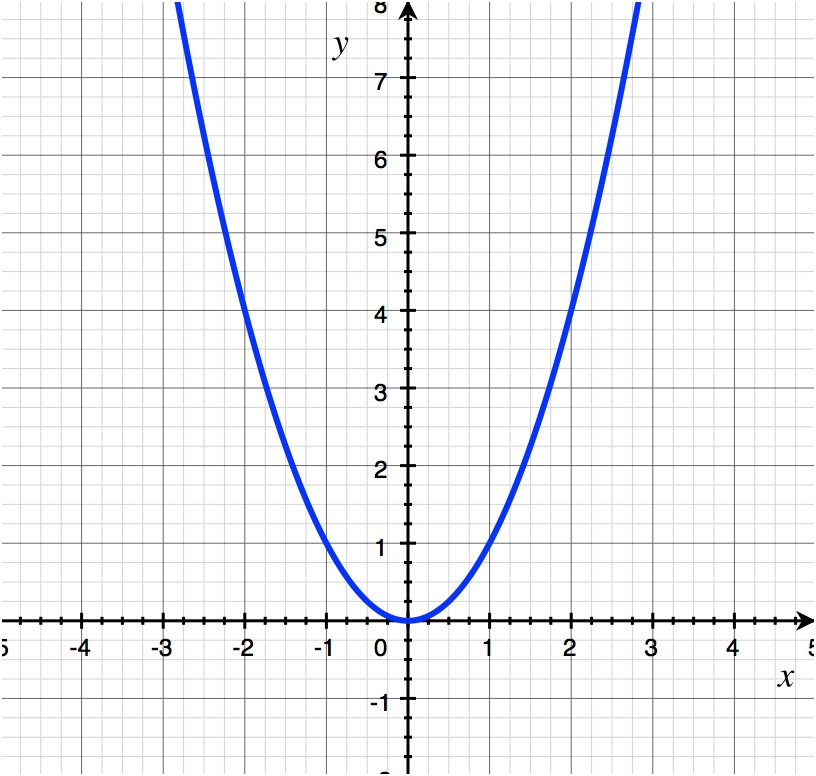
f(x) = x², x⁴, x⁶

parabolic family

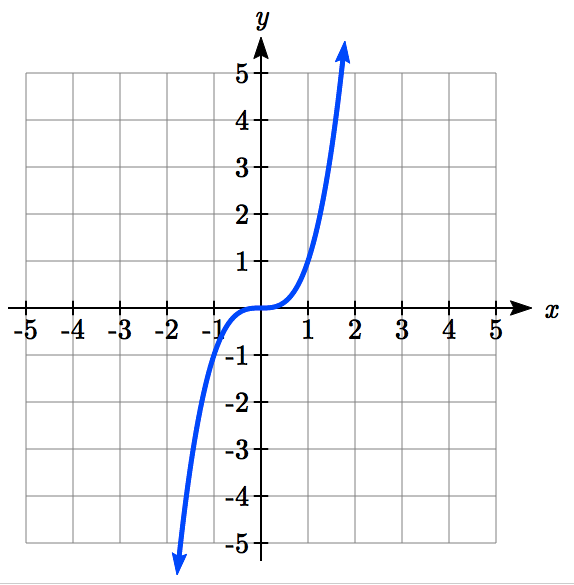
f(x) = x³, x⁵, x⁷

cubic family

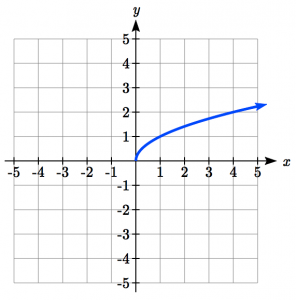
f(x) = x^1/2, x^1/4, x^1/6

square root family

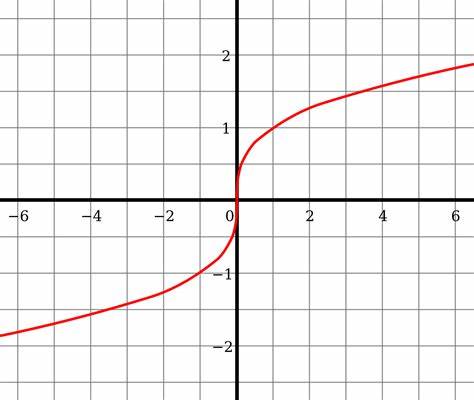
f(x) = x^1/3, x^1/5, x^1/7

cubic root family

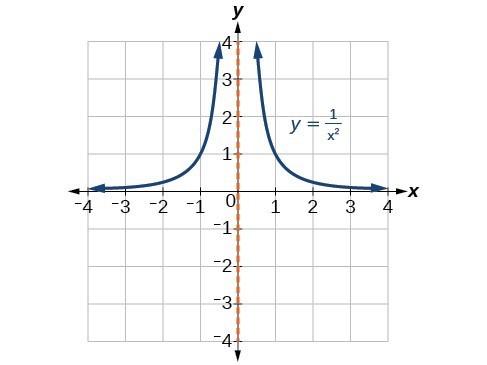
f(x) = x^-2, x^-4, x^-6

bell curve family

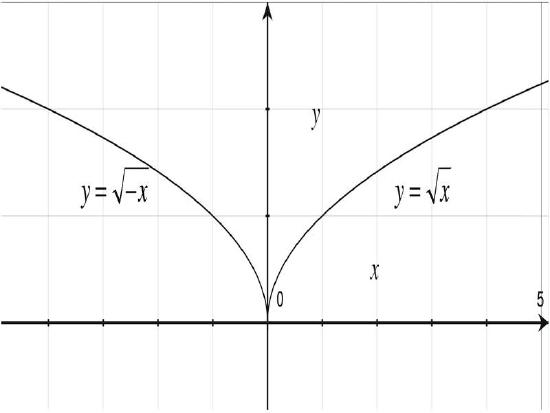
f(x) = x^2/3, x^4/5, x^6/7

Bird Family

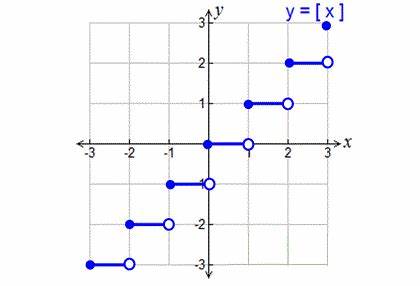
f(x) = [|x|]

greatest integer function

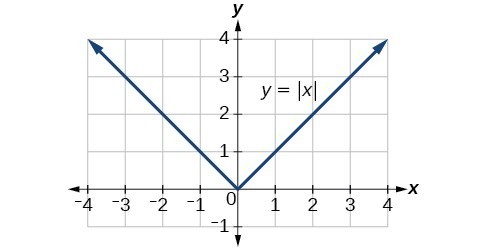
f(x) = |x|

absolute value

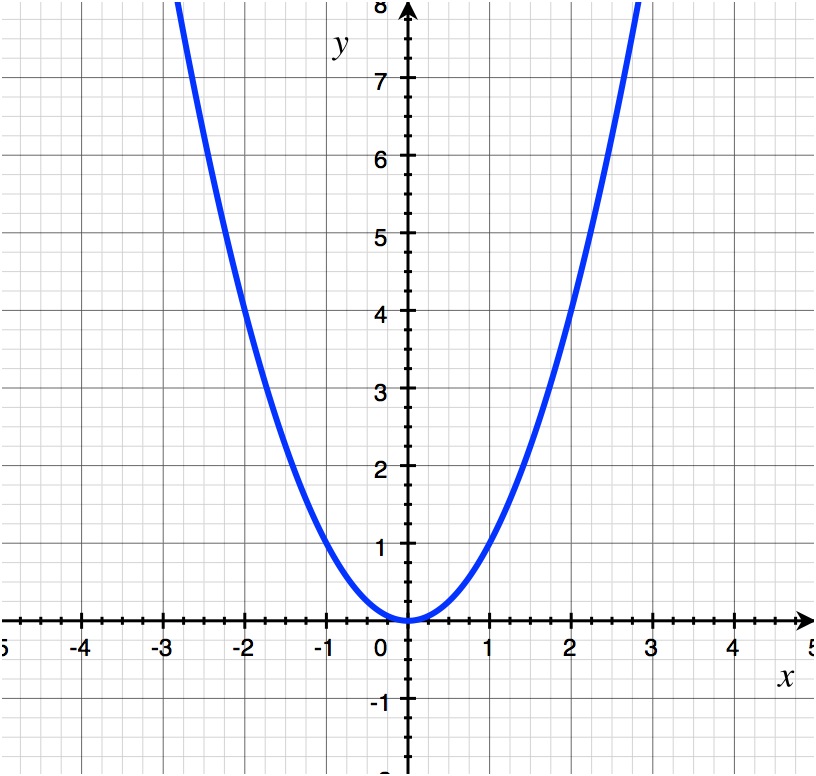
f(x) = ax² + bx + c

parabola family

Vertex of f(x) = ax² + bx + c?

Vertex → (h,k)

h = -b/2a

k = f(-b/2a)

f(x) = a_nxⁿ + a_n-1x^n-1 + .. a_{0; n is odd}

1) outside behavior → cubic

2) intercepts

3) relative extrema (n-1)

4) symmetry

f(x) = (a_nxⁿ + a_n-1x^n-1 + .. a_{0) /} (b_mx^m + b_m-1x^m-1 + .. b₀₎

1) asymptotes

2) intercepts

3) symmetry

4) plot points if needed

to find vertical asymptotes

set denominator of simplified rational expression to 0

to find horizontal asymptotes of rational functions

n=m, H.A. @ y=a/b

n<m, H.A. @ y = 0

n>m, no H.A.

f(x) = (c-x²)^1/2 , _c>0

circular function

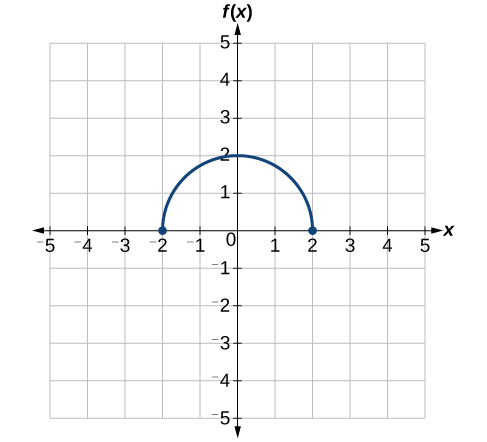
f(x) = (x²-c)^1/2 , _c>0

hyperbolic function

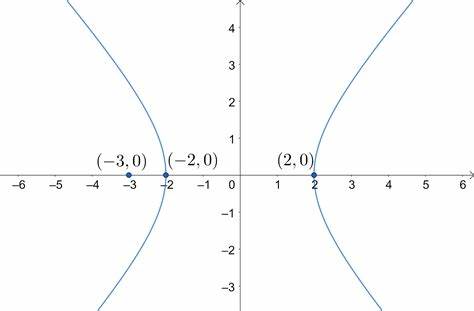
f(x) = (x²+c)^1/2

hyperbolic function