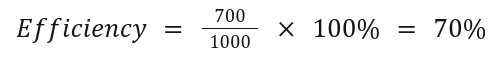1. Kinetic Energy (KE)

• Definition:

  • Energy an object possesses due to its motion.

• Formula:

  

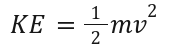
  • m: Mass (in kilograms, kg)

  • v: Velocity (in meters per second, m/s)

• Key Concept:

  • Kinetic energy depends on the square of velocity, meaning small increases in speed lead to significant increases in energy.

  • Doubling an object's velocity increases its kinetic energy by four times

• Importance:

  • Critical in analyzing motion, collisions, and momentum in physics.

• Applications:

  • Vehicle safety (e.g., analyzing collisions and braking distances).

  • Sports (e.g., calculating energy in projectiles like a baseball or soccer ball).

  • Engineering (e.g., turbines and engines).

• Example Problem:

  • A 5 kg object moves at 10 m/s. Find its kinetic energy.

    • Solution:

      

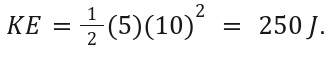
2. Gravitational Potential Energy (PE)

• Definition:

  • Energy stored in an object due to its height in a gravitational field.

• Formula:

  

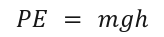
  • m: Mass (kg)

  • g: Gravitational acceleration (9.8 m/s2)

  • h: Height (m)

• Key Concept:

  • Directly proportional to mass and height.

• Importance:

  • Plays a key role in energy conservation and systems like roller coasters, pendulums, and hydroelectric power.

• Applications:

  • Hydropower (e.g., water stored in dams).

  • Roller coasters (e.g., analyzing height and speed transitions).

  • Space science (e.g., calculating escape velocity for rockets).

• Example Problem:

  • A 2 kg object is 5 m above the ground. Find its gravitational potential energy.

    • Solution:

      

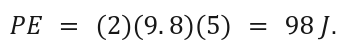
3. Elastic Potential Energy (PE)

• Definition:

  • Energy stored in elastic materials when stretched or compressed.

• Formula:

  

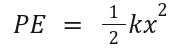
  • k: Spring constant (N/m)

  • x: Displacement from equilibrium position (m)

• Key Concept:

  • Increases quadratically with displacement.

• Importance:

  • Essential in analyzing springs, elastic bands, and other systems where energy is stored and released.

• Applications:

  • Suspension systems in vehicles.

  • Archery (e.g., energy stored in a stretched bowstring).

  • Trampolines (e.g., energy during compression and release).

• Example Problem:

  • A spring with k = 200 N/m is compressed by 0.1 m. Find its potential energy.

    • Solution:

      

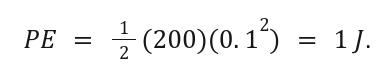
4. Thermal Energy

• Definition:

  • The total kinetic energy of particles in a substance, linked to its temperature.

• Key Concepts:

  • Higher temperatures result in greater particle motion.

  • Plays a key role in phase changes (e.g., melting, boiling).

• Importance:

  • Vital in understanding heat transfer methods (conduction, convection, radiation) and thermodynamics.

• Applications:

  • Heat engines (e.g., steam engines, car engines).

  • Climate science (e.g., understanding global temperature changes).

  • Daily life (e.g., cooking, insulation systems).

• Applications:

  • Engine efficiency, refrigeration, and climate systems.

5. Mechanical Energy

• Definition:

  • Total energy in a system from both kinetic (KE) and potential (PE) energy.

• Formula:

  

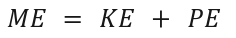
• Key Concept:

  • Remains constant in a closed system (ignoring friction or external forces).

• Importance:

  • Used in energy conservation laws to analyze physical systems like pendulums and roller coasters.

• Applications:

  • Pendulum motion (e.g., energy transformation between KE and PE).

  • Amusement park rides (e.g., analyzing energy in roller coasters).

• Example Problem:

  • A 3 kg object at a height of 4 m has a speed of 2 m/s. Find its total mechanical energy.

    • Solution:

      

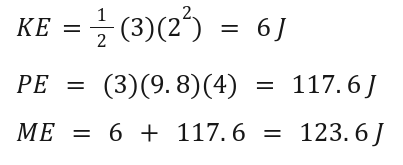
6. Work-Energy Theorem

• Definition:

  • Work done on an object equals the change in its kinetic energy.

• Formula:

  

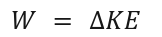
• Key Concept:

  • Links force, displacement, and energy changes.

• Importance:

  • Simplifies motion problems by focusing on energy changes rather than forces.

• Applications:

  • Launching a rocket (work increases kinetic energy).

  • Braking a car (negative work decreases kinetic energy).

• Example Problem:

  • A force does 50 J of work on a stationary object. What is its kinetic energy after the work is applied?

    • Solution:

      

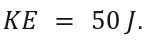
7. Conservation of Energy

• Definition:

  • Energy cannot be created or destroyed, only transformed between forms.

• Key Concepts:

  • Total energy in a closed system remains constant.

  • Examples include conversions between kinetic, potential, and thermal energy.

• Importance:

  • Fundamental principle in physics and engineering.

• Applications:

  • Power generation (e.g., potential energy of water in dams to electrical energy).

  • Space exploration (e.g., converting chemical energy of fuel to kinetic energy of rockets).

• Example Problem:

  • A pendulum at its highest point has PE = 100 J. At its lowest point, what is its kinetic energy (ignoring friction)?

    • Solution:

      

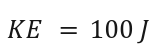
8. Energy Transformations

• Definition:

  • Conversion of energy from one form to another (e.g., potential to kinetic).

• Key Concepts:

  • Observed in systems like pendulums, roller coasters, and power plants.

  • Energy loss as heat or sound often accompanies transformations.

• Importance:

  • Critical for analyzing real-world systems and energy efficiency.

• Applications:

  • Renewable energy systems (e.g., solar panels converting light to electrical energy).

  • Daily life (e.g., batteries powering devices).

9. Power (P)

• Definition:

  • The rate at which work is done or energy is transferred.

• Formula:

  

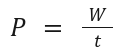
  • W: Work (J)

  • t: Time (s)

• Key Concept:

  • Measured in watts (W, where 1 W = 1 J/s).

• Applications:

  • Electrical systems (e.g., power ratings of appliances).

  • Sports (e.g., analyzing athletes’ performance).

• Example Problem:

  • A motor does 500 J of work in 10 s. Find its power output.

    • Solution:

      

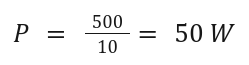
10. Efficiency

• Definition:

  • A measure of how much useful energy or work output is achieved compared to energy input.

• Formula:

  

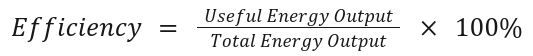
• Key Concept:

  • No machine is 100% efficient due to energy losses as heat or friction.

• Applications:

  • Evaluating machine performance (e.g., engines, electric generators).

  • Energy systems (e.g., renewable energy plants).

• Example Problem:

  • A machine uses 1000 J of energy and produces 700 J of useful work. Find its efficiency.

    • Solution: