Geometry: 3d and 2d shapes

Recommended: Graph paper, formulas, TI 84 calculator. Use writing and flashcard modes, answer with definition.

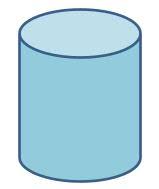
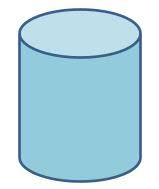
What shape is this?

Cylinder

How do you find the diameter using the circumference?

Divide the circumference by PI.

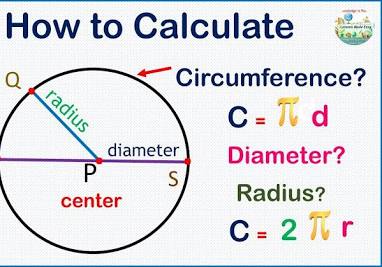
How do you convert inches to feet?

Divide the number by 12.

How do you convert feet to inches?

Multiply the number by 12

A cone with a height of 8 inches and a diameter of 6. What is the volume to the nearest tenth?

75.4 in

A wooden toy block can be modeled by a pyramid with a square base, as shown below. The height of the block is 17.4 cm and the square base has a side length of 8.2 cm.

Find the volume of the wooden toy block and round your answer to the nearest hundredth.

389.99

Samuel wants to fill an empty fish tank with water. The fish tank is in the shape of a rectangular prism with the dimensions 25cm, 24 cm and 125 cm.

He uses a cylindrical bucket with a diameter of 20 cm to fill the tank. Determine and state the maximum number of buckets of water, filled to an exact height of 26 cm, Samuel can put into the fish tank before it overflows.

9 buckets

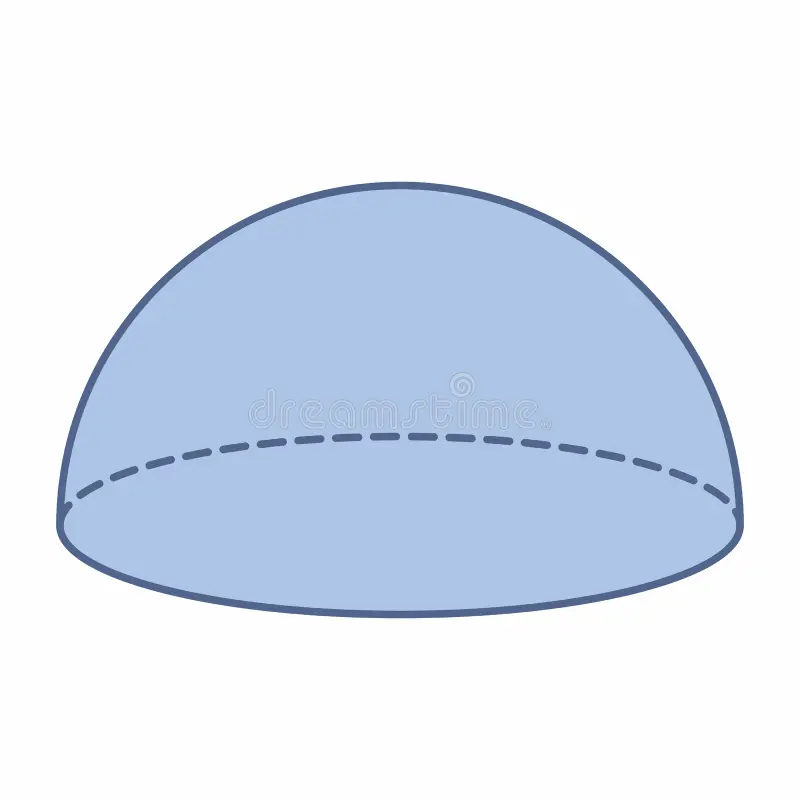
What shape is this?

Hemisphere

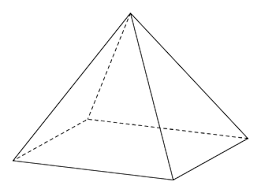
What shape is this?

Pyramid

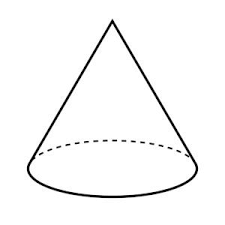
What shape is this?

cone

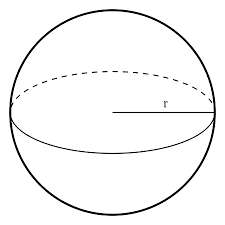
What shape is this?

Sphere

What shape is this?

Rectangular prism

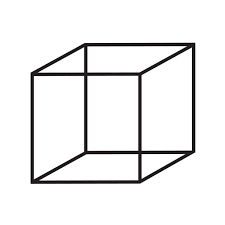
What shape is this?

cube

What is a radius?

A radius is a line segment or its length that extends from the center of a circle or sphere to its circumference or surface, and it is always half the length of the diameter.

What is a diameter?

The diameter of a circle is a straight line segment that passes through the circle's center, connecting two points on the circle's opposite edges. It is always twice as much as the radius.

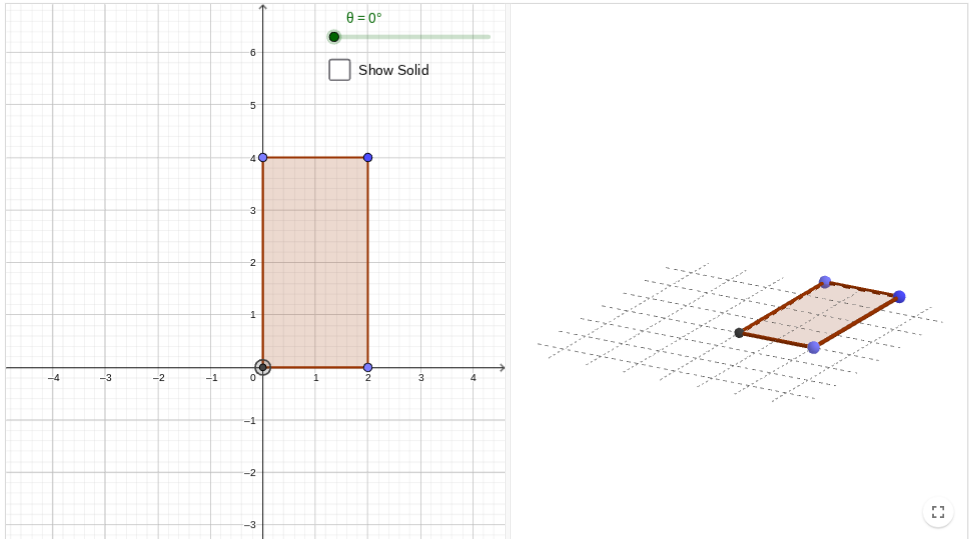
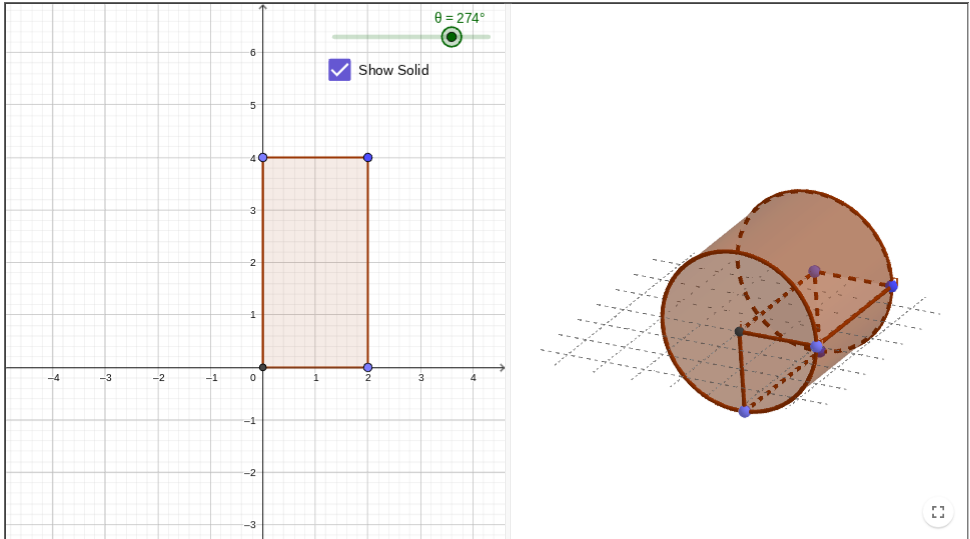
What 3d shape will form after rotating the rectangle continuously around one of its vertical sides (out of the flat plane)

What is its radius and diameter?

A cylinder.

radius = 2

diameter = 4

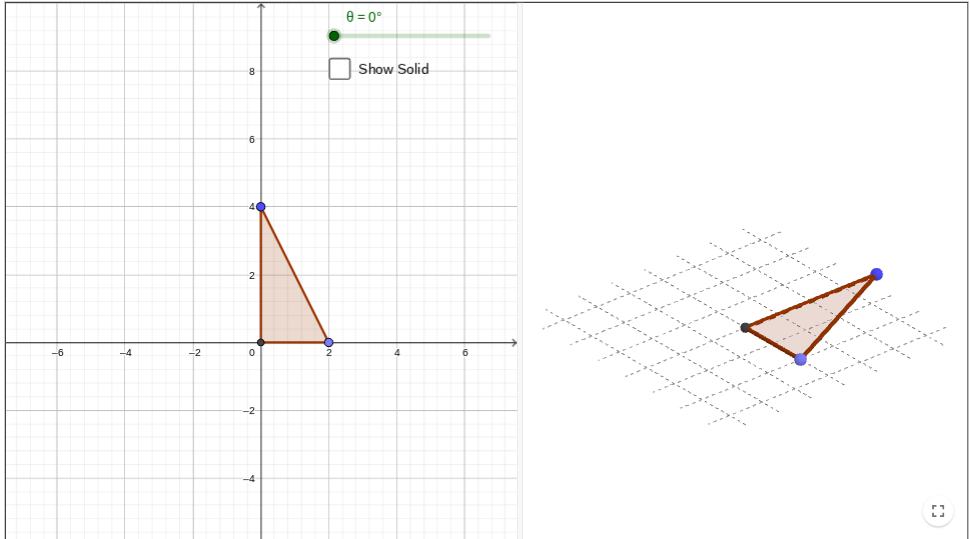
What 3d shape will form after rotating the triangle continuously around one of its vertical sides (out of the flat plane).

What is its radius and diameter?

A cone.

Radius = 2

Diameter = 4

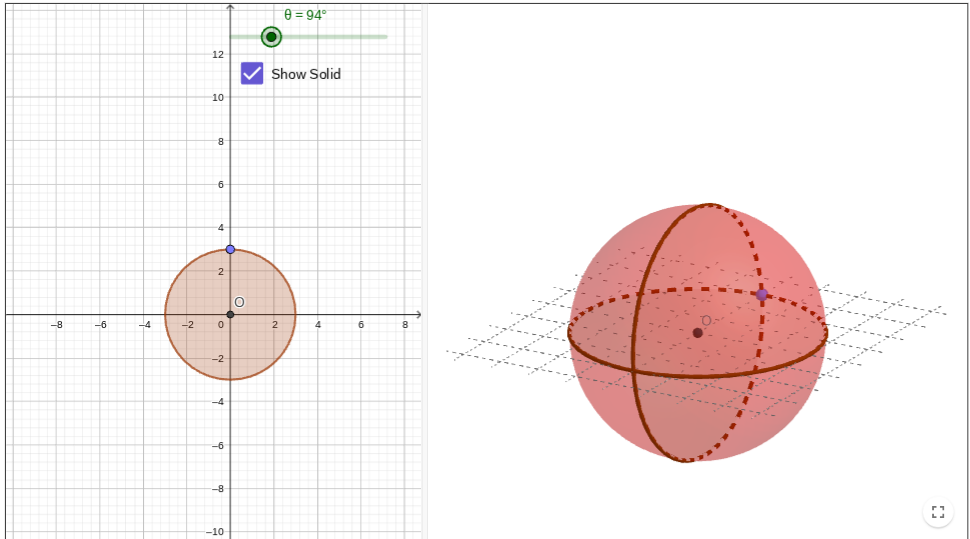
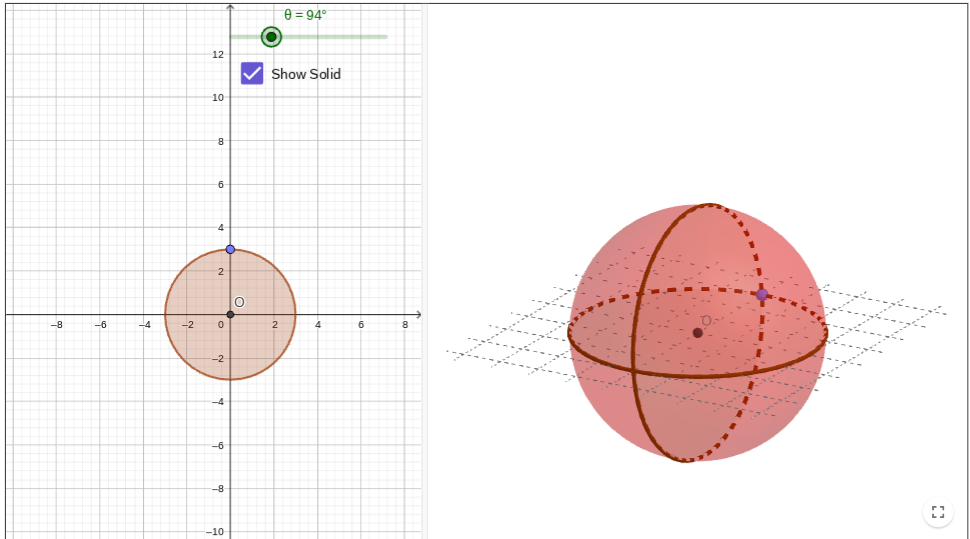
at 3d shape will form after rotating the circle continuously around one of its vertical sides (out of the flat plane).

What is its radius and diameter?

A sphere.

Radius = 3

diameter = 6

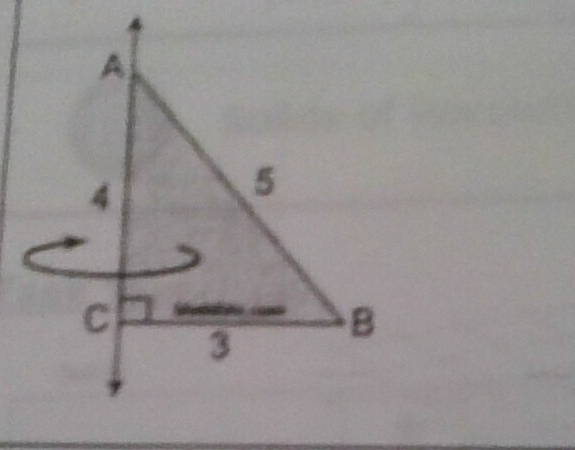
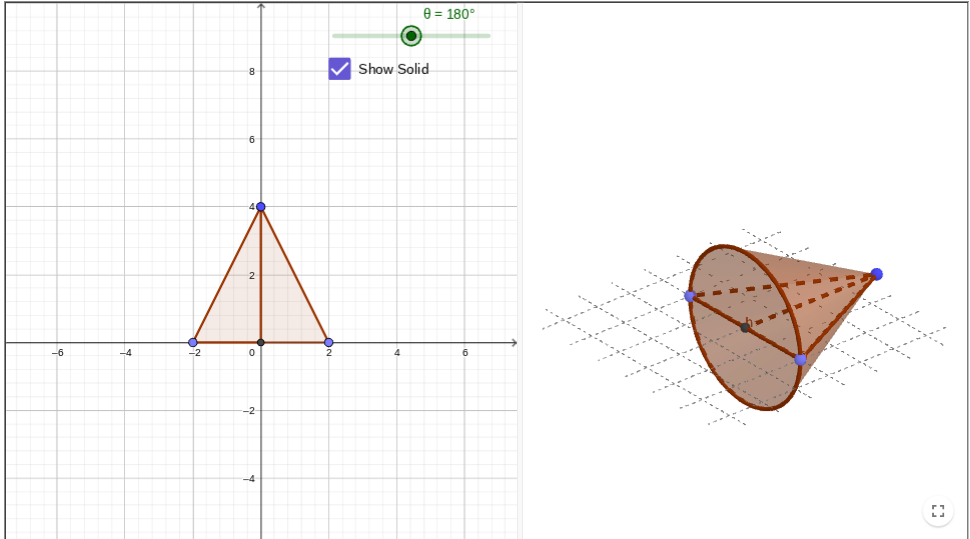
Rotate Triangle ABC continuously around line AC. What shape does it become?

What is its Radius, diameter and height?

A cone.

Height = 4

Radius= 3

diameter = 6

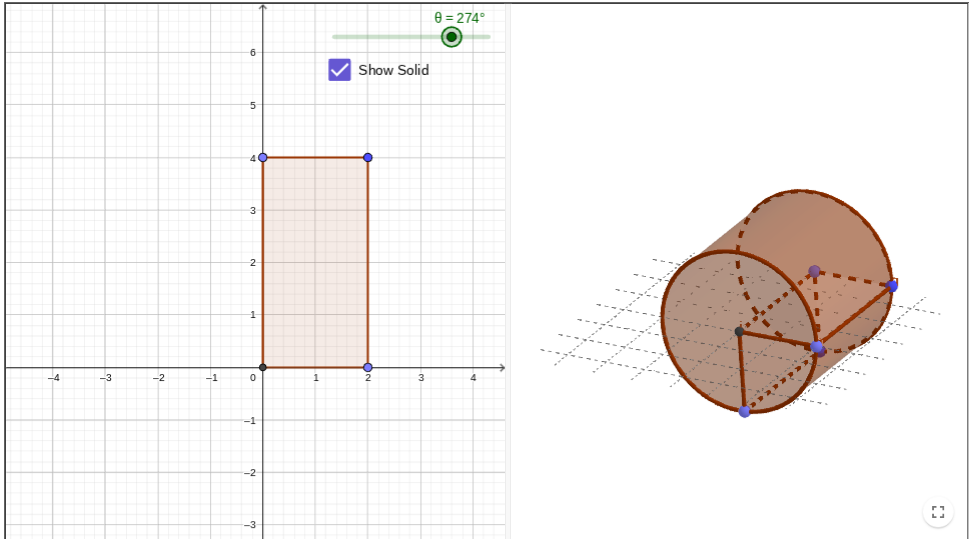
Rotate the rectangle continuously around the vertical line. What shape does it become?

What is its Radius, diameter and height?

It becomes a cylinder.

Height = 4

Radius = 3

Diameter = 6

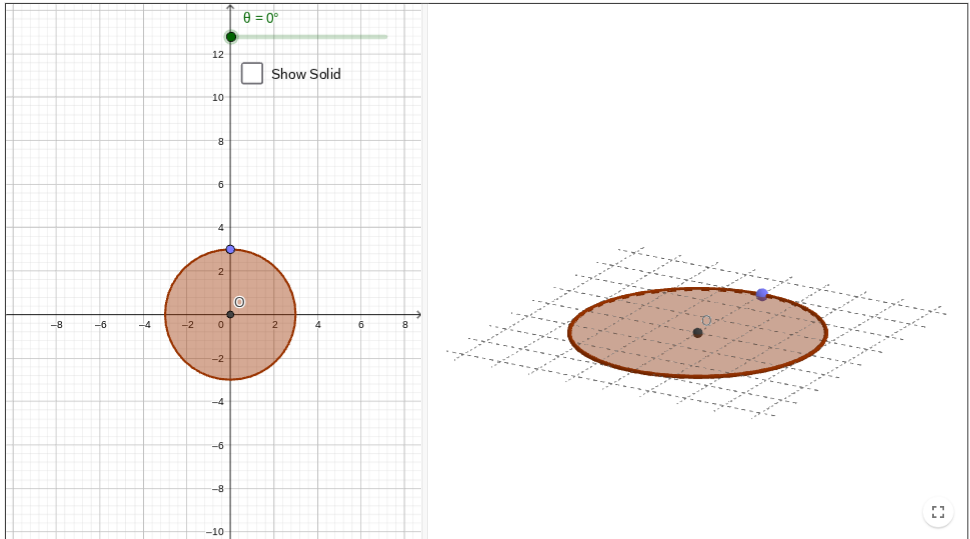
If a circle is continuously rotated about its diameter, it becomes a…

Sphere

If a half circle is continuously rotated about its diameter, it becomes a…

Sphere

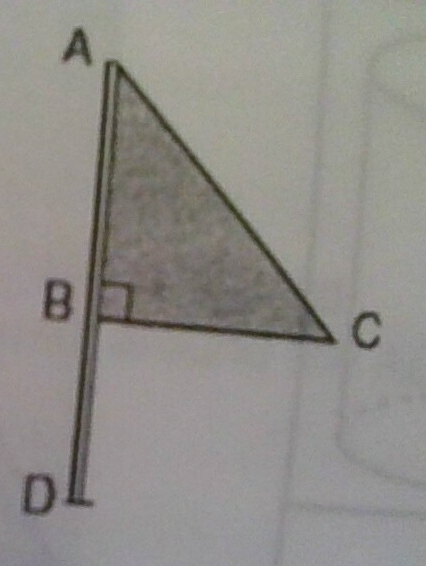
Triangle ABC represents a metal flag on pole AD, as shown in the accompanying diagram. On a windy day the triangle spins around the pole so fast that it looks like a three dimensional shape.

What shape would the spinning flag create?

A cone.

A student has a rectangular postcard that he folds in half lengthwise. Next, he rotates it continuously about the folded edge. Which three-dimensional object is generated by this rotation.

A cylinder

If the rectangle below is continuously rotated about side w, which solid figure is formed?

A cylinder

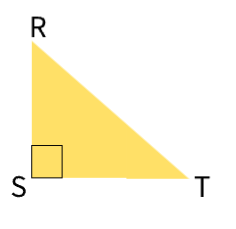
Which object is formed when the triangle RST is rotated around leg RS ?

A cone

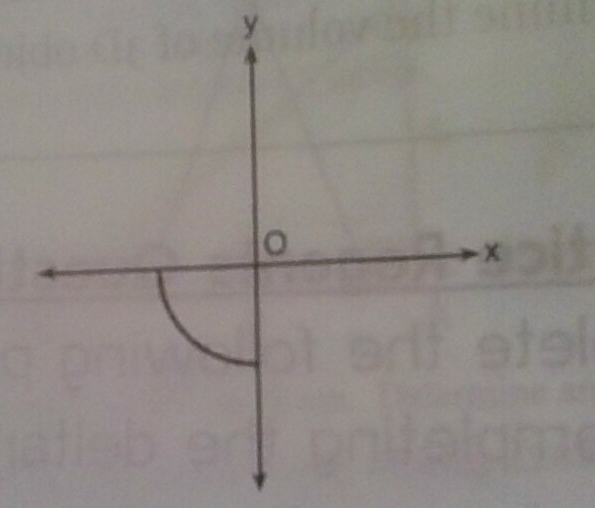
Circle O is centered at the origin. In the diagram, a quater of circle O is graphed.

Which tree-dimensional figure is generated when the quarter circle is continuously rotated about the y-axis?

A hemisphere

If a rectangle is continuously rotated around one of its sides, what is the three-dimensional figure formed?

A cylinder

An equilateral triangle is continuously rotated around one of its altitudes. The three-dimensional object formed is a…

cone

A circle is continuously rotated about its diameter. Which three dimensional object will be formed?

A sphere

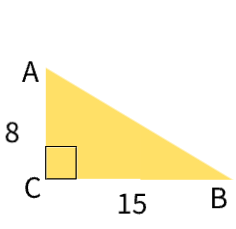
As shown in the diagram, right triangle ABC has side lengths of 8 and 15.

If the triangle is continuously rotated about AC, the resulting figure will be…

1). A right cone with a radius of 15 and a height of 8

2) a right cone with a radius of 8 and a height of 15

3) a right cylinder with a radius of 15 and a height of 8

4) a right pyramid with a radius of 8 and a height of 15

1). A right cone with a radius of 15 and a height of 8

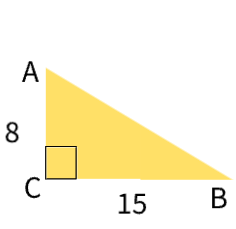
Find the volume of RIght triangle ABC if it is rotated continuously about side AC.

Hint: use a formula

600π

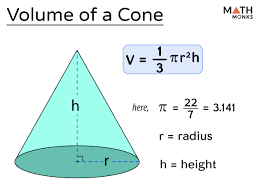
When looking for the volume in a 3dd shape what does answering (in terms of pi) mean?

Leaving the answer with the π symbol in it.

What is the cone formula?

V = (1/3)πr²h

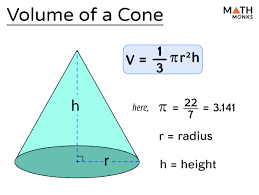
What is the sphere formula?

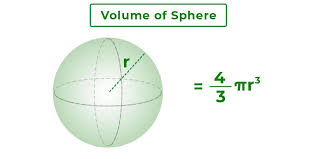
V = 4/3πr³

Square MATH has a side length of 7 inches. What three-dimensional object will be formed by continuously rotating square MATH around side AT, and what is its radius? Find the volume of the shape as well.

Hint: you need a formula

A cylinder with a radius of 7, and its volume is 1077.57

(Note: a square is the same length on all sides)

Which three dimensional figure will result when a rectangle 6 inches long and 5 inches wide is continuously rotated about the longer side?

1) a rectangular prism with a length of 6 inches, width of 6 inches and height of 5 inches.

2) a rectangular prism with a length of 6 inches, width of 5 inches, and height of 5 inches.

3) A cylinder with a radius of 5 inches and a height of 6 inches.

4) a cylinder with a radius of 6 inches and a height of 5 inches.

Then, find the volume of that shape.

3) A cylinder with a radius of 5 inches and a height of 6 inches.

Volume is roughly 471.239

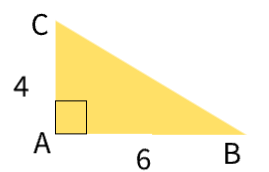
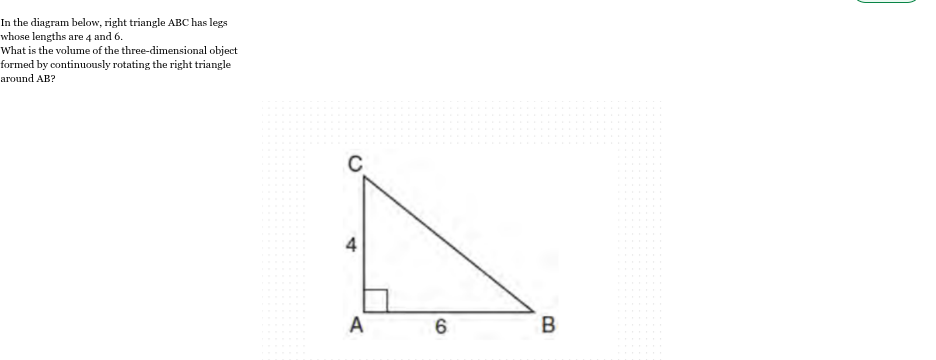
In right triangle CAB, CA = 4 and AB = 6

Determine and state, to the nearest tenth, the volume of the three-dimensional solid formed by rotating CAB continuously around AB.

V = 100.5

What is the cylinder formula?

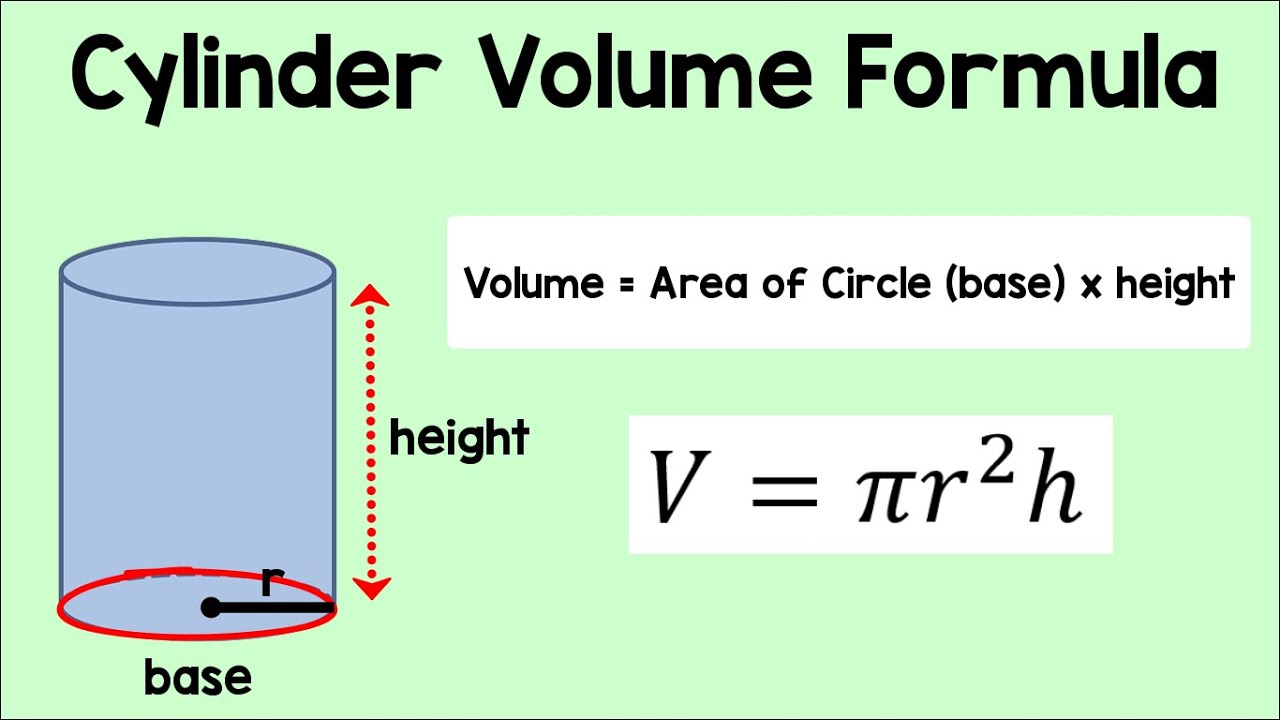
V = πr²h

What is the cylinder formula?

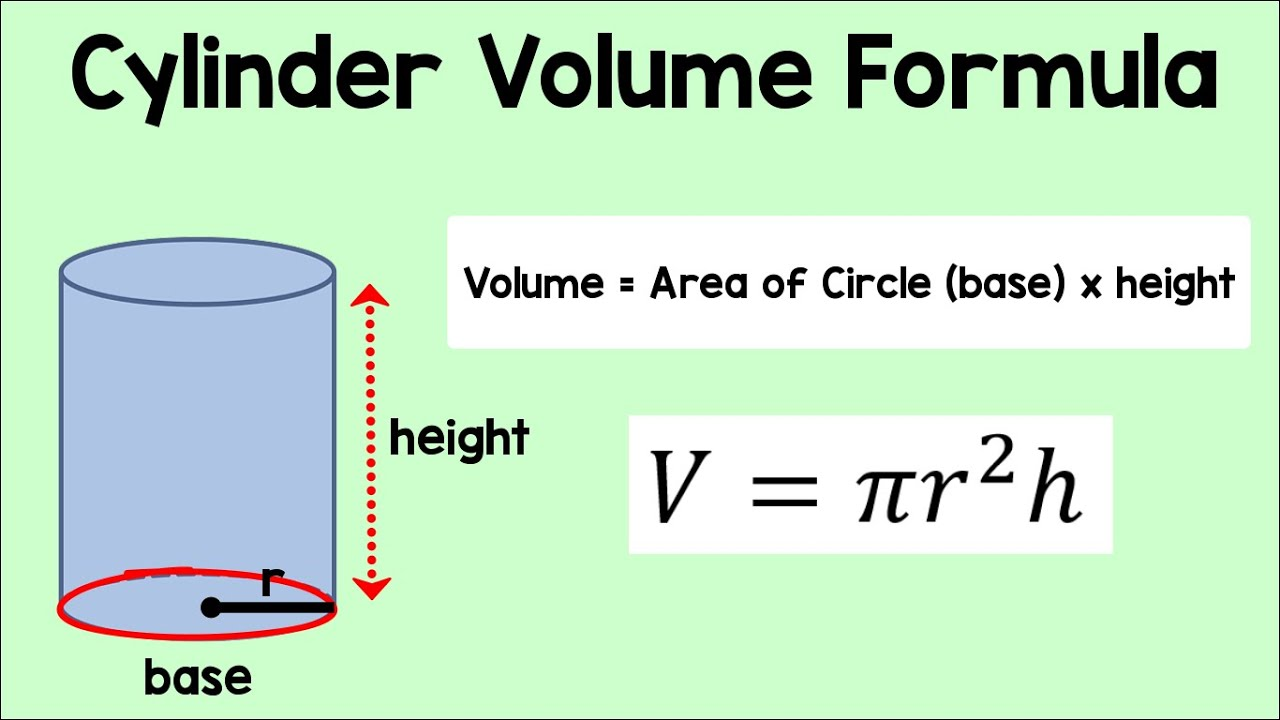
V = πr²h

What is the cylinder formula?

V = πr²h

What is the cone formula?

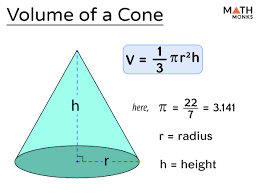
V = (1/3)πr²h

What is the cone formula?

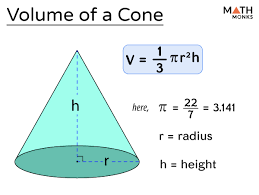
V = (1/3)πr²h

What is the sphere formula?

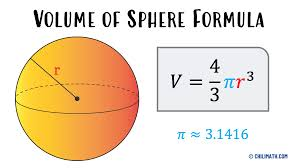
V = (4/3)πr³

What is the sphere formula?

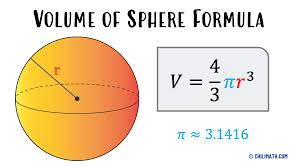
V = (4/3)πr³

46.1 units³

33.5 units³

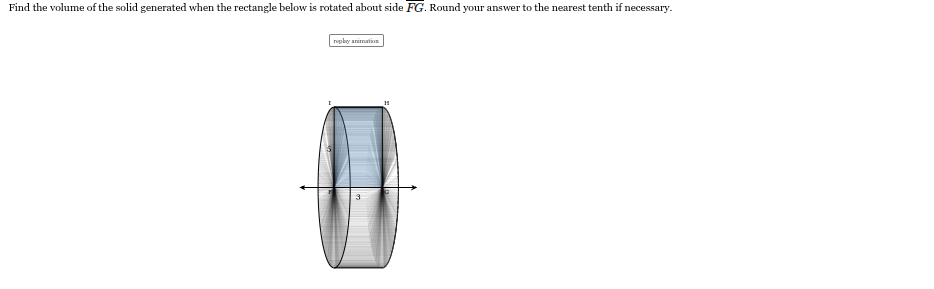
235.6 units³

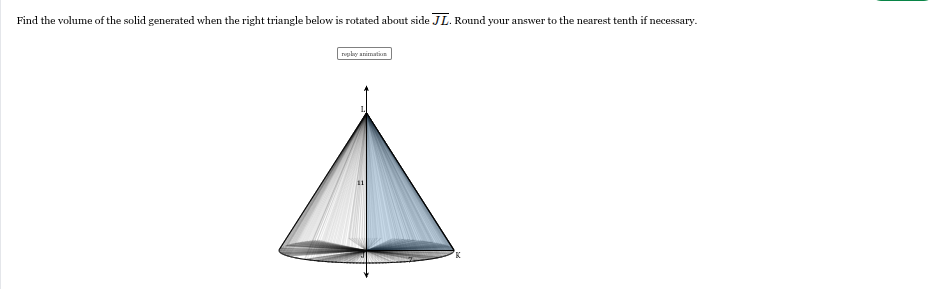
564.4 units³

(in terms of PI)

32π

(Read image)

1) long side

2) short side

3) vertical line of symmetry

4) horizontal line of symmetry

3) vertical line of symmetry

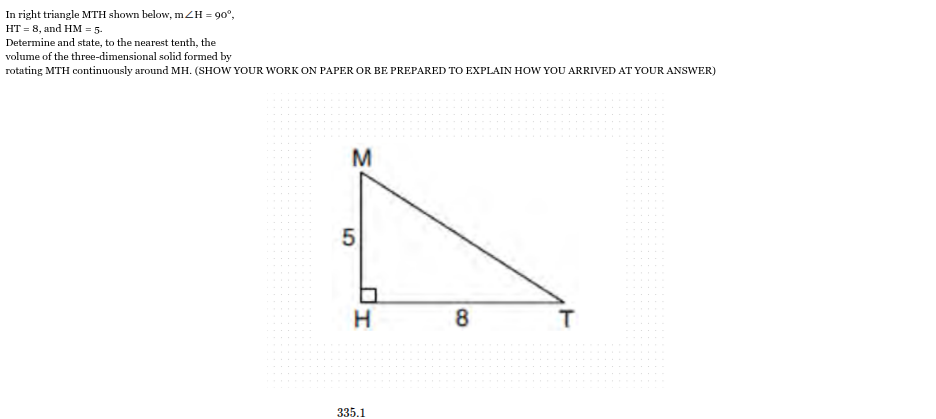
335.1

An equilateral triangle is continuously rotated
around one of its altitudes. The three-dimensional
object formed is a…

CONE

What is the formula for a rectangular (or square) pyramid?

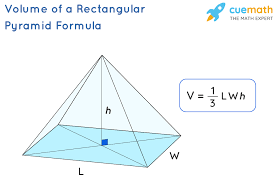
What is the formula for a rectangular (or square) pyramid?

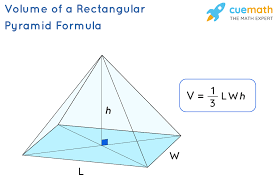
What is the formula for a rectangular (or square) pyramid?

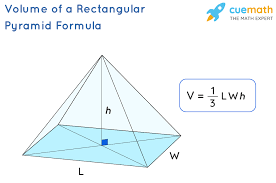
What is the formula for a rectangular (or square) prism?

What is the formula for a rectangular prism (or square)?

What is the formula for a rectangular (or square) formula?

What does B represent?

The area of the starting shape. For a cylinder that would be PI x r² as that's the area of a circle. For a rectangular prism its L x W

What does B represent?

The area of the starting shape. For a cylinder that would be PI x r² as that's the area of a circle. For a rectangular prism its L x W

Darnell Models a cup with a cylinder drawing. He measured the diameter of the cup to be 10 cm and the height to be 9 cm.

If Darnell fills the cup with water to a height of 8 cm, what is the volume of the water in the cup, to the nearest cubic centimeter?

628 cm³

Tennis balls are sold in cylindrical cans with the balls stacked one on top of the other. A tennis ball has a diameter of 6.7 cm. To the nearest cubic centimeter, what is the minimum volume of the can that holds a stack of 4 tennis balls?

1) 236

2) 282

3) 564

4) 945

4) 945

A small can of soup is a right circular cylinder with a base diameter of 7 cm and a height of 9 cm. A large container is also a right cylinder with a base diameter of 9 cm and a height of 13 cm.

Determine and state the volume of the small can and the volume of the large container to the nearest cubic centimerer

Than state the minimum number of small cans that must be opened tofill the large container.

Small can: 346 cm³

Large container: 827 cm³

Minimum amount of cans: 3

A regular pyramid has a square base whose side measures 6 inches.

If the altitude of the pyramid measures 12 inches, what is its volume in cubic inches? Round to the nearest cubic centimeter if needed,

144 cm³

The pyramid of Memphis, Tennessee stands 107 yards tall and has a square base whose side is 197 yards long.

What is the volume of the pyramid of Memphis, to the nearest cub yard?

1) 751,818

2) 1,384,188

3) 4,255,259

4) 6,105,214

2) 1,384,188

A regular pyramid has a square base. The perimeter of the base is 36 inches and the height of the pyramid is 15 inches. What is the volume of the pyramid in cubic inches?

V = 405 in³

A water cup in the shape of a cone has a height of 4 inches and a maximum diameter of 3 inches. What is the volume of the water in the cup, to the nearest tenth of a cubic inch, when the cup is filled to half its height?

1.2 in³

Remember since the height is cut in half due to the shape of a cone the diameter is cut in half too, thus the radius.

What is the volume of a right circular cone that has a height of 7.2 centimeters and a radius of 2.5 centimeters, to the nearest tenth of a cubic centimeter?

47.1 cm³

Jaden is comparing two cones. The radius of the base of cone A is twice as large as the radius of the base of cone B. The height of cone B is twice the height of cone A. The volume of cone A is

1) twice the volume off cone B

2) four times the volume of cone B

3) equal to the volume of cone B

4) equal to half the volume of cone B

1) twice the volume off cone B

Sally and Mary both get ice cream from an Icecream Truck. Sally’s ice cream is served as a cylinder with a diameter of 4 cm and a total height of 8 cm. Mary’s ice cream is served as a cone with a diameter of 7 cm and a total height of 12.5 cm. Assume that ice cream fills Sally’s cylinder and Mary’s cone.

Who was served more ice cream, Mary or Sally? Determine and state how much more is served in the larger ice cream than the smaller ice ream to the nearest cubic centimeter.

Mary was served about 60 cm³ more ice cream than Sally

What is the volume of a hemisphere that has a diameter of 12.6 cm, to the nearest tenth of a cubic centimeter?

523.7 cm³

A storage tank is in the shape of a cylinder with a hemisphere on top. the highest point on the inside of the storage tank is 13 meters above the floor of the storage tank, and the diameter inside the cylinder is 8 meters. Determine and state to the nearest cubic meter, the total volume inside the storage tank.

586 m³

A pyramid has a square base a height of 7 and a volume of 84.

what is the length of the side of the base?

1) 6

2) 12

3) 18

4) 36

1) 6

The base of a pyramid is a rectangle with a width of 4.6 cm and a length of 9 cm. What is the height, in centimeters, of the pyramid if its volume is 82.8 cm³

^{1) 6}

^{2) 2}

^{3) 9}

^{4) 18}

1) 6

A cone has a volume of 108π and a base diameter of 12. What is the height of the cone?

2) 9

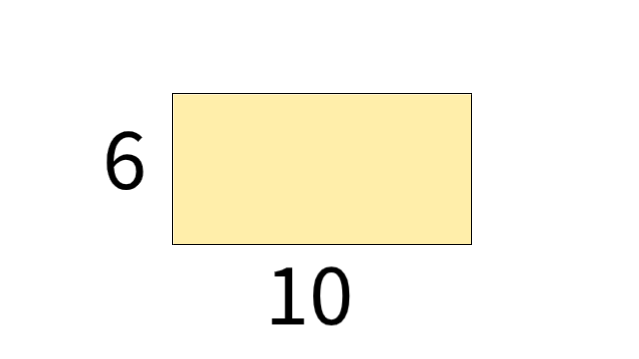
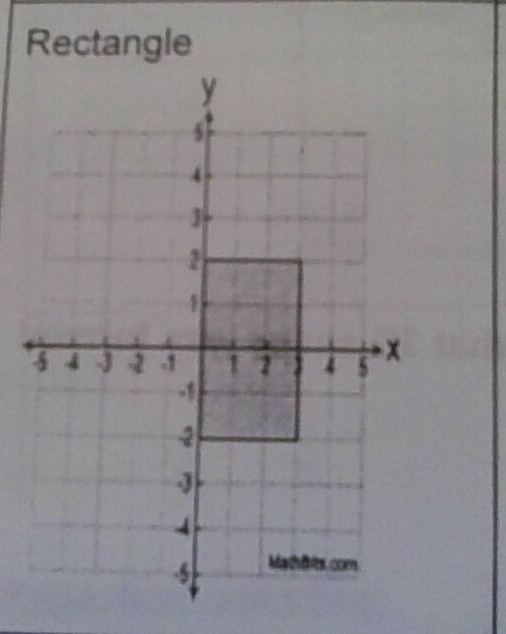
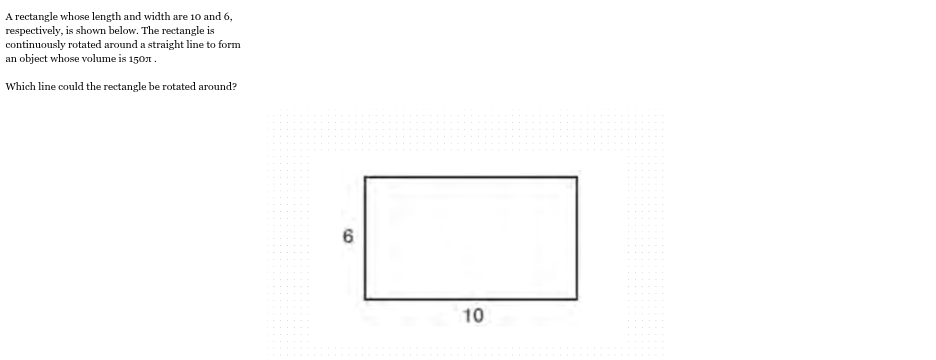
A rectangle whose length and width are 10 and 6, respectviely, is shown. The rectangle is continuously rotated around a straight line to form an object whose volume is 150π

Which line could the rectangle be rotated around?

1) a long side

2) a short side

3) the vertical line of symmetry

4) the horizontal line of symmetry

3) the vertical line of symmetry

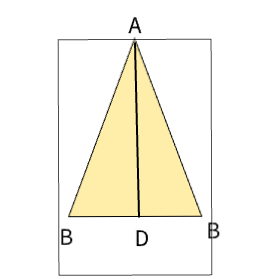
In isosceles triangle ABC shown, AB roughly equals AC, and altitude AD is drawn.

The length of AD is 12 cm and the length of BC is 10 cm… Determine and state, to the nearest cubic centimeter, the volume of the solid formed by continuously rotating ABC about AD

314 cm³

What does cubic mean?

Basically it just means you have to follow up with the power of three at the end of your unit. in³, cm³, m³, etc.

What is the area of a circle?

πr²

What does πr² represent?

The area of a circle

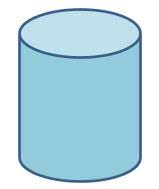
What information would you need to calculate the volume of this solid?

The cylinder formula, its height, and its diameter/radius

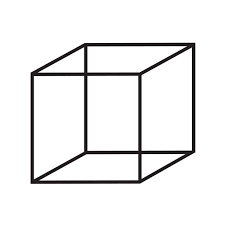
What information would you need to calculate the volume of this solid.

Its height or length or width

Note: since its a cube the length, height and width are the same

What information would you need to calculate the volume of this solid.

Its height, length and width

What is the volume of a cylinder, in cubic centimeters, with a height of 12 centimeters and a base diameter of 20 centimeters? Round to the nearest tenths place.

3769.9 cm³

What is the volume of a cylinder, in cubic meters, with a height of 2 meters and a base diameter of 8 meters? Round to the nearest tenths place.

100.5 m³

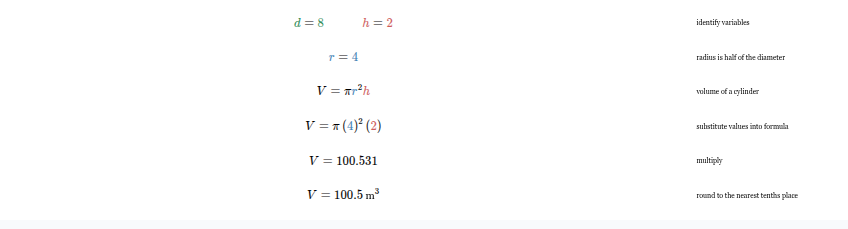
What is the volume, in cubic centimeters, of a rectangular prism with a height of 4 centimeters, a width of 11 centimeters, and a length of 8 centimeters?

V = 352 cm³

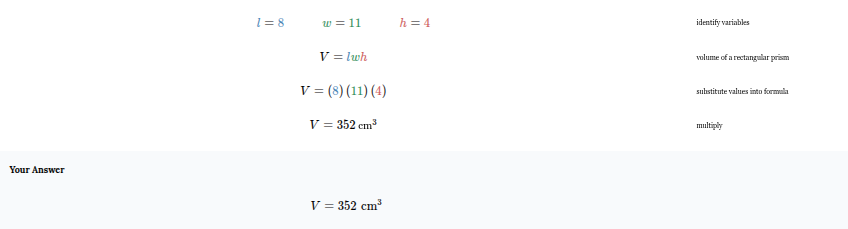
Find the volume of a right circular cone that has a height of 18.1 in and a base with a diameter of 18.7 in. Round your answer to the nearest tenth of a cubic inch.

1657 in³

Find the volume of a right circular cone that has a height of 11.9 in and a base with a radius of 14 in. Round your answer to the nearest tenth of a cubic inch.

2442.5 in³

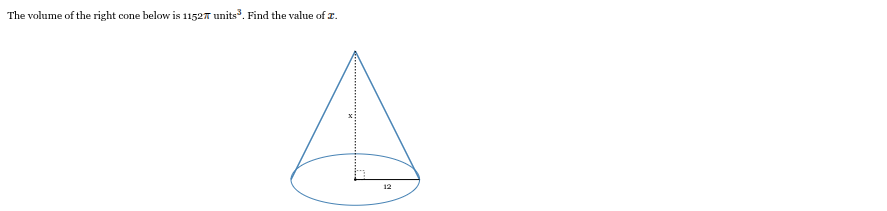
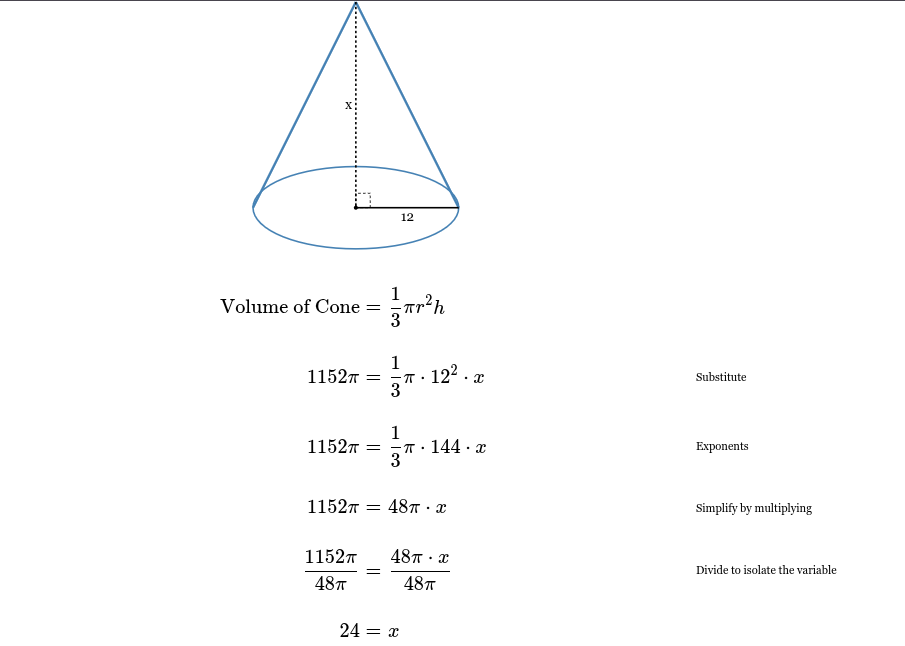
The volume of the right cone is 1152π units³. Find the value of x.

x = 24

Find the volume of a pyramid with a square base, where the side length of the base is 7.5 cm and the height of the pyramid is 10.2 cm. Round your answer to the nearest tenth of a cubic centimeter.

V = 191.3 cm³

Find the volume of a pyramid with a square base, where the side length of the base is 6.1 m and the height of the pyramid is 4.7 m. Round your answer to the nearest tenth of a cubic meter.

58.3 m³

What is the volume of a sphere with a radius of 8.8 in, rounded to the nearest tenth of a cubic inch?

2854.5 in³

What is the volume of a hemisphere with a diameter of 56.7 in, rounded to the nearest tenth of a cubic inch?

47721.9 in³

Sarah models the volume of a popcorn box as a right rectangular prism. Its dimensions are 3 ¾ in by 3 in by 7 1/2 in. How many cubic inches of popcorn would it hold when full? Round your answer to the nearest tenth if necessary.

84.4 in³

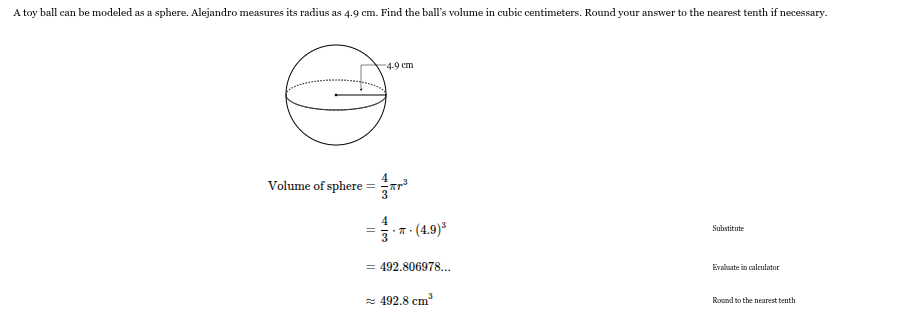
A toy ball can be modeled as a sphere. Alejandro measures its radius as 4.9 cm. Find the ball’s volume in cubic centimeters. Round your answer to the nearest tenth if necessary.

V = 492.8 cm³

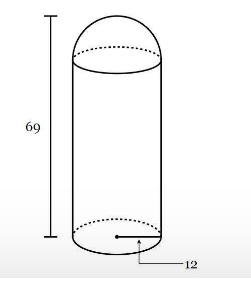
A grain silo can be modeled as a right cylinder topped with a hemisphere. Find the volume of the silo if it has a height of 69 m and a radius of 12 m. Round your answer to the nearest tenth if necessary. 

29405.3 m³

How do you find the radius of a sphere if you only have its height?

The height of a sphere is the same as its diameter, or twice its radius. you could use the formula h = 2r. In this case you would divide the height by 2 to get your answer.

How do you find the height of a sphere if you only have its radius?

The height of a sphere is the same as its diameter, or twice its radius. you could use the formula h = 2r

How do you find the height of a hemisphere if you only have its radius?

The height and radius of a hemisphere is the same, just like a squares width and length.