PSAD

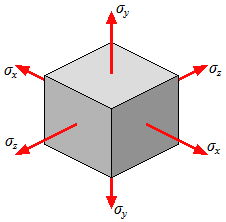
Multi-Axial Strain formula

\epsilon_x = \frac{1}{E} [\sigma_x - \nu(\sigma_y + \sigma_z)]

Thermal Deformation Formula

\delta_T = \alpha \cdot L \cdot \Delta T

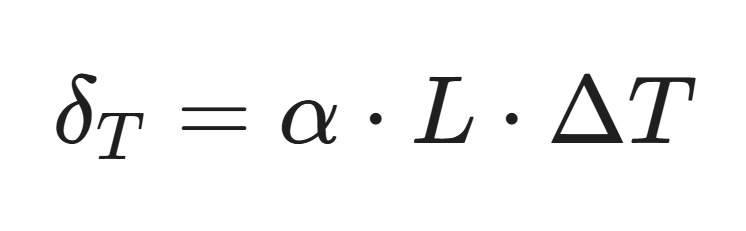
Coefficient of Linear Thermal Expansion (α) for Steel

\alpha=11.6\times10^{-6}

Deformation Formula

\delta = \frac{PL}{AE}

Angle of Twist Formula

\theta = \frac{TL}{JG}

Springs in Parallel

K_{eq}=K_1+K_2+K_3+\ldots+K_{n}

Springs in Series

\frac{1}{K_{eq}}=\frac{1}{K_1}+\frac{1}{K_2}+\frac{1}{K_3}+\ldots+\frac{1}{K_n}

Spring Constant (K) formula

K = \frac{P}{\delta}

or

K = \frac{AE}{L}

Torsional Shear Stress formula

\tau = \frac{Tr}{J}

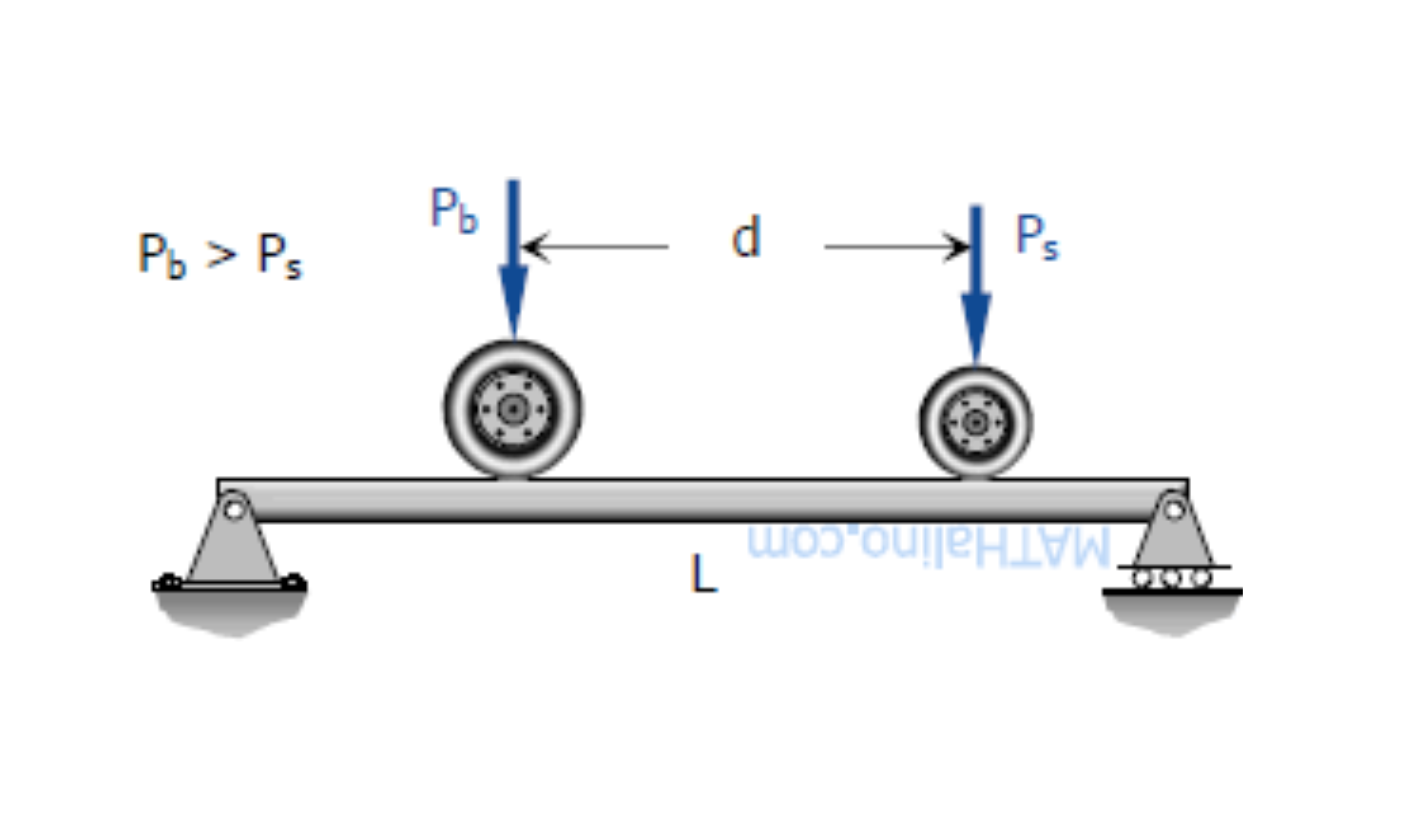
Moment for 2 Moving Loads

M_{max} = \frac{(PL - P_s d)^2}{4PL}

Moment-Curvature Equations

\kappa = \frac{1}{\rho} = \frac{M}{EI}

\rho = \frac{EI}{M}

Specific Shear Stress formula

\tau = \frac{VQ}{Ib}

fv,max for rectangular sections

\tau_{max}=\frac{3V}{2A}

fv,max for circular sections

\tau_{max}=\frac{4V}{3A}

fv,max for hollow circular sections

\tau_{max}=\frac{4V}{3A}\left(1+\frac{Dd}{D^2 + d^2}\right)

Shear Flow q formula

q=\frac{T}{2A_{o}}

Shear Stress in terms of Shear Flow

\tau=\frac{T}{2A_{o}t}

Cylinder Tank, Longitudinal and Tangential Stress

Longitudinal

\sigma_{L}=\frac{PD}{4t}

Tangential
\sigma_{C}=\frac{PD}{2t}

Cylinder Tank, Longitudinal and Tangential Stress

\sigma=\frac{PD}{4t}

Degree of Determinacy

Beams

i = r - 3n

Truss

i = (m + r) - 2j

Frames

i=(3m+r)-3j

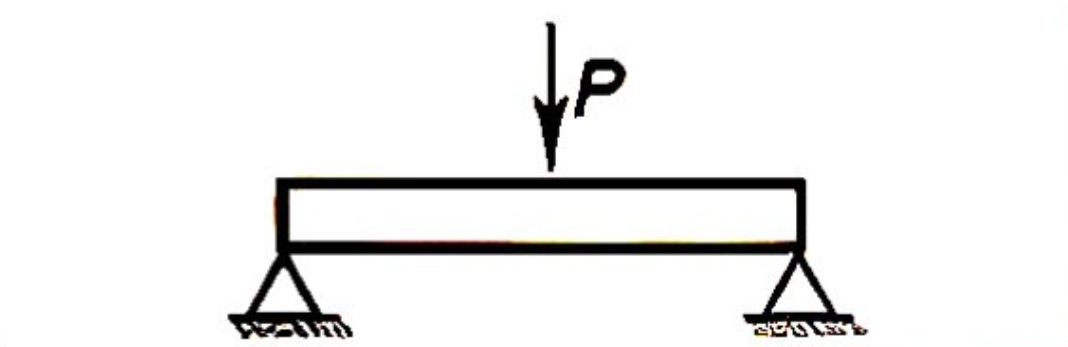
M_{max} = \frac{PL}{4}

\delta_{max} = \frac{PL^3}{48EI}

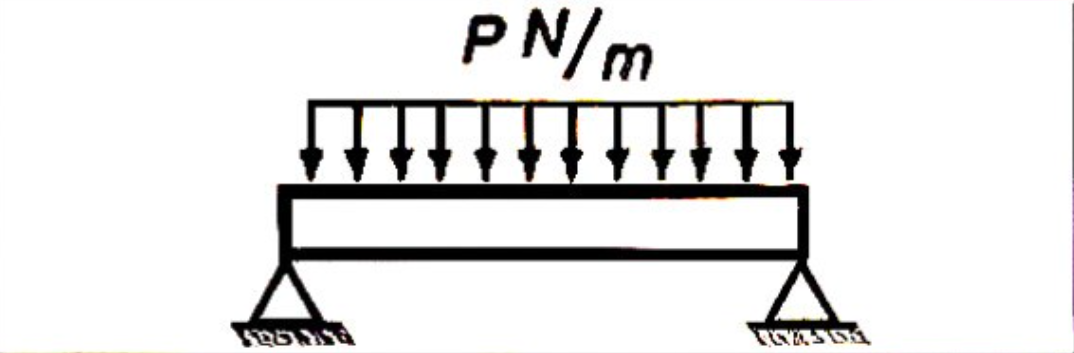
M_{max} = \frac{wL^2}{8}

\delta_{max} = \frac{5wL^4}{384EI}

M_{max} = -PL

\delta_{max} = \frac{PL^3}{3EI}

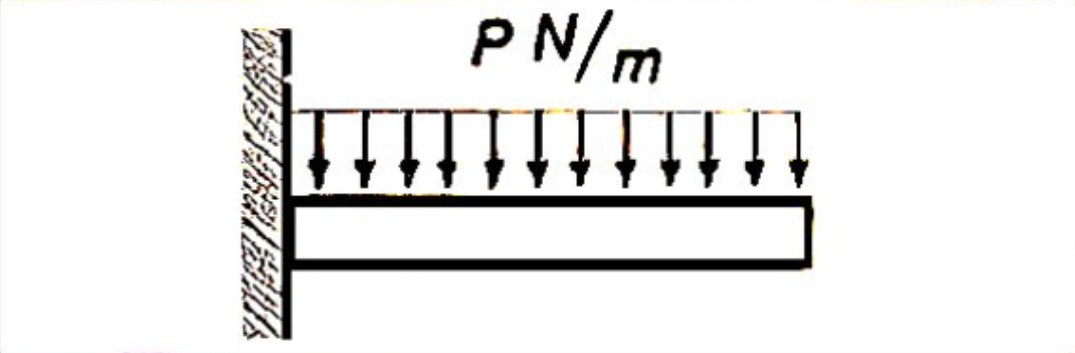
M_{max} = -\frac{wL^2}{2}

\delta_{max} = \frac{wL^4}{8EI}

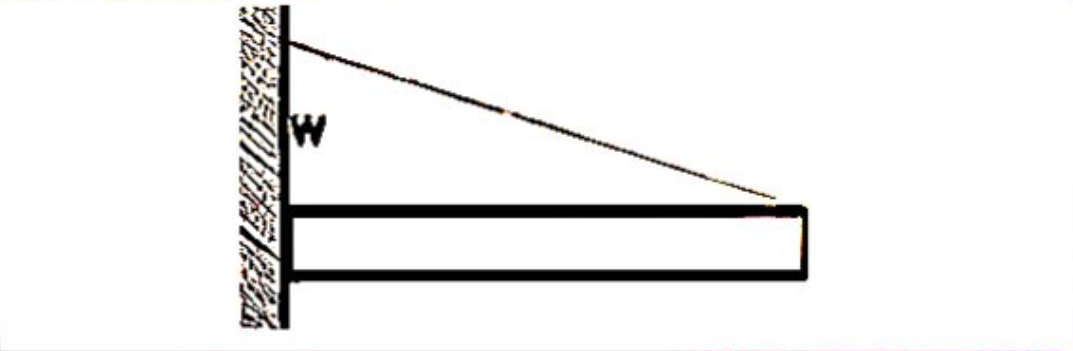
M_{max} = -\frac{wL^2}{6}

\delta_{max} = \frac{wL^4}{30EI}

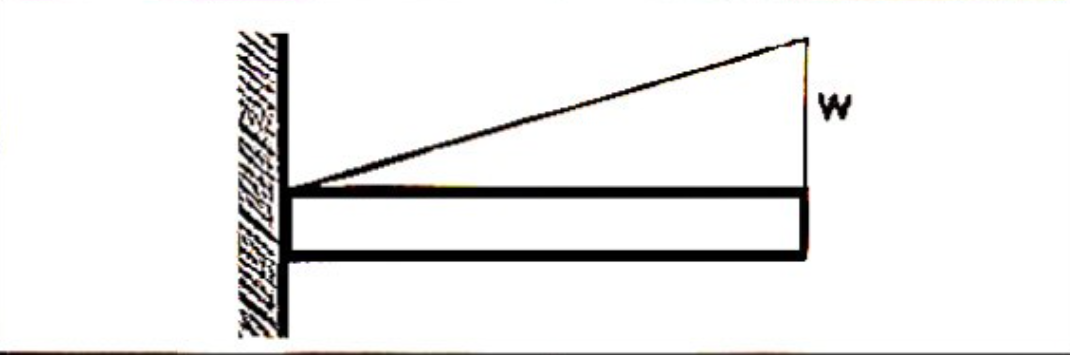
M_{max} = -\frac{wL^2}{3}

\delta_{max} = \frac{11wL^4}{120EI}

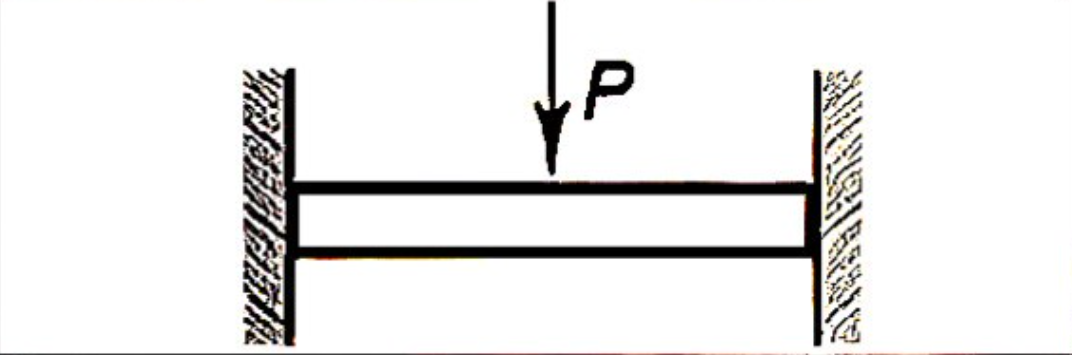
M_{max(+)} = \frac{PL}{8}

\delta_{max} = \frac{PL^3}{192EI}

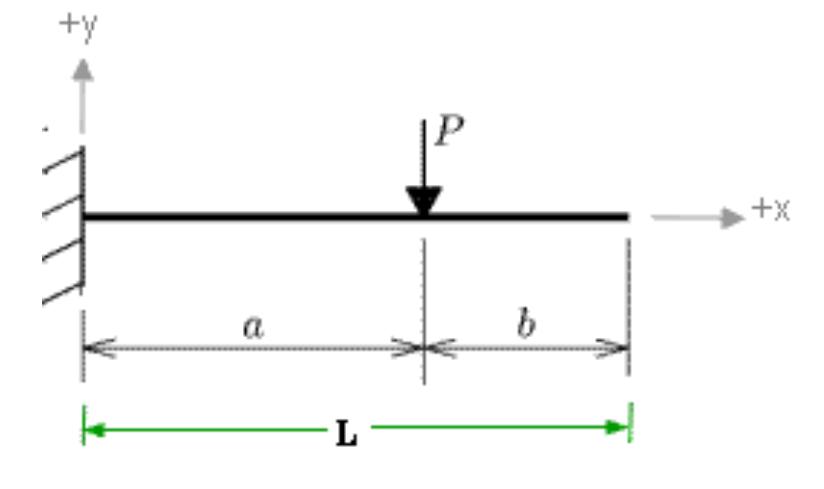
\delta_{max} = \frac{3Pa^2L - Pa^3}{6EI}

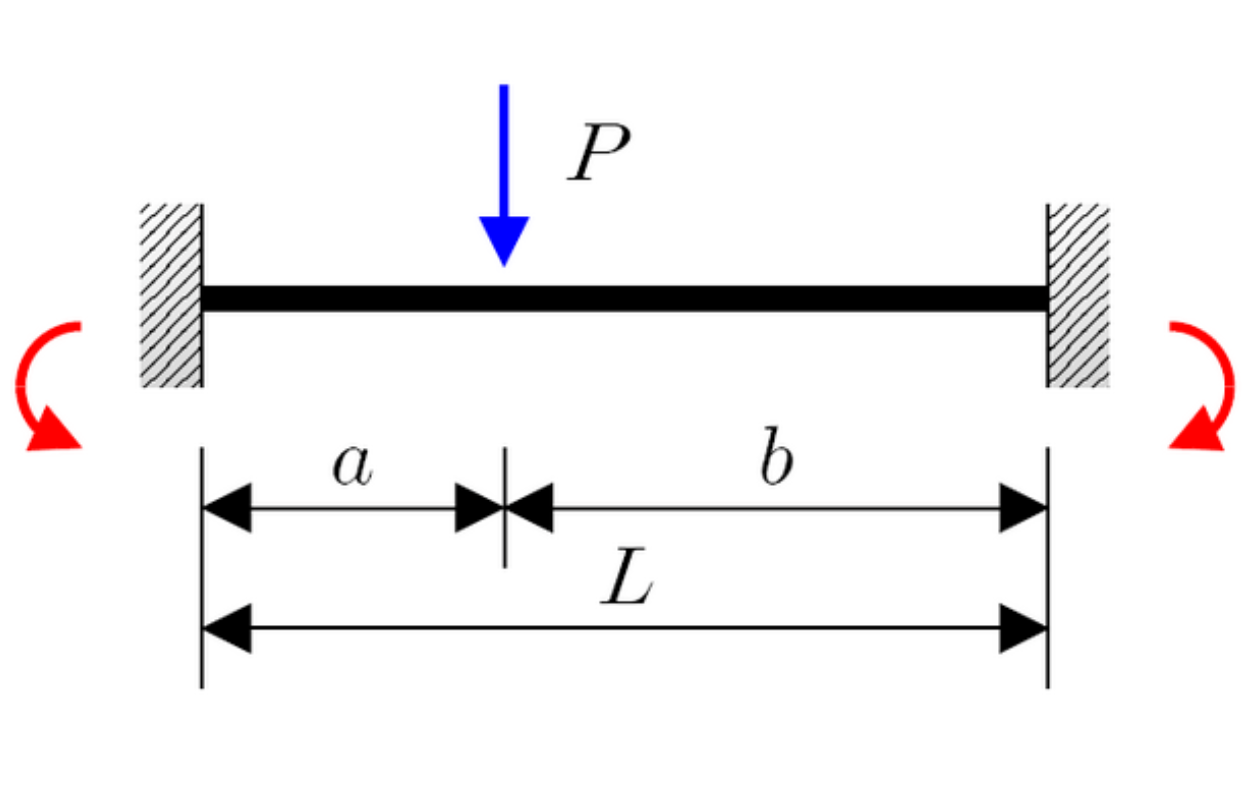
M_{A}=\frac{Pab^2}{L^2}

M_B = \frac{Pa^2b}{L^2}
R_A = \frac{Pb^2(3a + b)}{L^3}

R_B = \frac{Pa^2(a + 3b)}{L^3}

Tensile Strength (Gross Section Yielding)

P = 0.60 F_y A_g

Tensile Strength (Net Section Rupture)

P = 0.50 F_u A_n

Staggered Factor formula

\frac{s^2}{4g}

s - parallel to the force

g - perpendicular to the force

Block Shear formula

P = 0.5 F_u A_{nt} + 0.3 F_u A_{nv}

Length of Throat

0.707t

Ix of Bolts

i_x = \sum y^2

Ix of Welds

i_x = \sum \left( \frac{L^3}{12} + Ly^2 \right)

Caltech for Bolted Connections

\vec{R}=\left|\frac{P}{n}\angle\theta+\frac{T}{J}(y-xi)\right|

Caltech for Welded Connections

\vec{R}=\left|\frac{P}{L}\angle\theta+\frac{T}{J}(y-xi)\right|