5.2 - Marshallian externalities & multiple equilibria

Marshallian externalities

Local positive externalities that increase with size of industry

Lead to geographical agglomeration

• Local knowledge spillovers

• Input-output linkages

• L market pooling etc

Static model - can switch equilibria with out any fundamental changes

• Dynamic CA changes fundamentals

Marshallian externalities (ME) model - Harrison & Rodriguez-clare (2010) - Assumptions

Small open economy

2 sectors & 1 FofP (L)

• Sector 1 has constant RtS (& no externalities)

• Sector 2 has ME (constant RtS at firm level but L can have increasing productivity)

Marshallian externalities (ME) model - Harrison & Rodriguez-clare (2010) - Results

Under certain conditions, multiple equilibria arise

Equilibria in complete specialisation in 2 superior to 1

• Economy has latent advantage in 2 but due to coordination failures it fails to exploit it (specialises in 1)

As externalities take time to realise, countries may have dynamic CA in sector not currently specialised in

• may justify protection / IIP - policy can swap it to new CA without any fundamental changes

Marshallian externalities (ME) model - Harrison & Rodriguez-clare (2010) - maths

1: L produces λ1 units of 1

2: L produces λ2(1+αMin(L^bar,L₂)

• externalities increasing with employment but exhausted when L in sector teaches L^bar

• θ ≡ 1 + αL^bar > 1 = max benefits from clustering in 2 1 + α = max benefits

If L₂ > L^bar the max level of productivity = θλ2

p* is world price of good 2 p*=p*₂ / p*₁

Marshallian externalities (ME) model - Harrison & Rodriguez-clare (2010) - specialisation in good 1

wage = λ₁p*₁ if specialised in good 1

unit cost of producing 2 (with no cluster benefits) = w/λ₂ = p*

Hence, complete specialisation in good 1 is an equilibrium if and only if p* <= λ₁/ λ₂

• p*=p*₂ / p*₁ = (w/λ₂) / (w/λ₁) = λ₁/ λ₂

Marshallian externalities (ME) model - Harrison & Rodriguez-clare (2010) - specialisation in good 2

wage = λ₂p*₂θ

Hence, complete specialisation in good 2 is an equilibrium if and only if θp* >= λ₁/ λ₂

• p*=p*₂ / p*₁ = (w/θλ₂) / (w/λ₁) = λ₁/θλ₂

Marshallian externalities (ME) model - Harrison & Rodriguez-clare (2010) - multiple equilibria

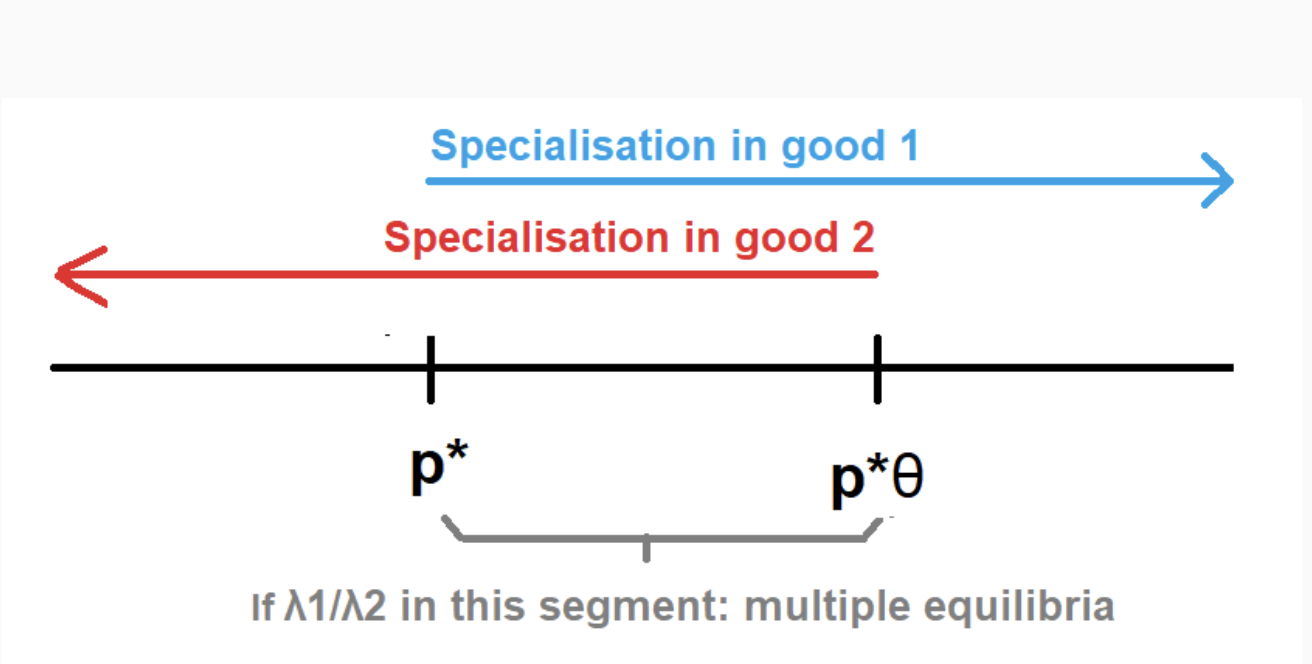
There is multiple equilibria if and only if:

p* <= λ₁/ λ₂ <= θp* CONDITION 1

• θ > 1 as α > 0 & θ = 1 + α

If no externalities then p* only equilibrium

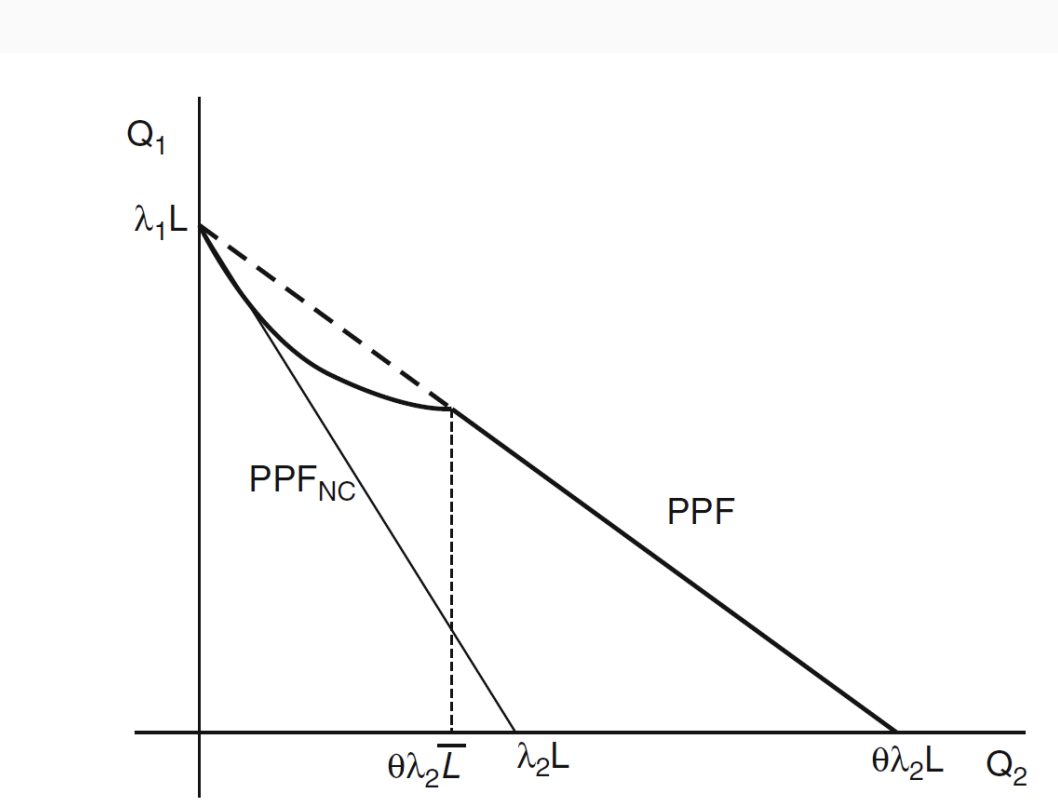
Marshallian externalities (ME) model - Harrison & Rodriguez-clare (2010) - multiple equilibria graph

θ = λL (determined by L assigned to each sector)

Externality causes line to turn as L increase = externality UP = Productivity UP

Turns until limit of L^bar then back to linear PPF with 1 factor

Marshallian externalities (ME) model - Harrison & Rodriguez-clare (2010) - wages in multiple equilibria

If complete specialisation in 1: w = λ₁p*₁

2: w = λ₂p*₂θ

Therefore if condition 1 satisfied then w₂ > w₁

Marshallian externalities (ME) model - Harrison & Rodriguez-clare (2010) - latent CA (LCA)

LCA in good i if: OC of this good when ME realised < p^w

• For good 1: λ₂θ/ λ₁ <= 1/p*

• For good 2: λ₁/ λ₂θ <= p*

Specialisation may still occur in 1 as nation has static CA in it and so isnt realising all ME

Marshallian externalities (ME) model - Harrison & Rodriguez-clare (2010) - Using a tariff

By using a tariff, consumers only see modified p - may cause switch to better equilibrium → Welfare rises

If p2 price increased enough by t → OC of producing 1 high enough to switch specialisation to 2

• p = p*t₂ = p*₂t₂ / p*₁ > p*

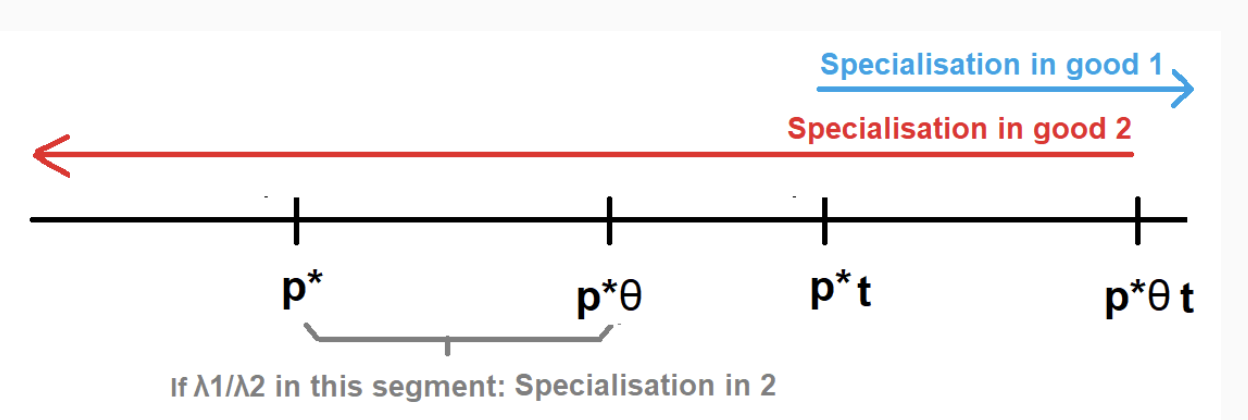
Once economy has switched specialisation then tariff can be removed

Marshallian externalities (ME) model - Harrison & Rodriguez-clare (2010) - Endogenous prices

Previously we have assumed p* is exogenous - in reality p* is determined by RoW productivity

Rich nations already enjoy lower costs of cluster in 2

• lower costs shown by p*

For developing nation to have LCA in 2 it must have deep parameters to sustain advantage

• α & L^bar need to be higher than in developed

• Large developing can realise more ME as shift moreL

• Technology affects α but unlikely to only affect developing

Marshallian externalities (ME) model - Harrison & Rodriguez-clare (2010) - Endogenous prices implications on model

Assume 2 is K & H intensive relative to 1

Specialising in 1 = low levels of K&H + lower TFP

By shifting specialisation to 2 through policy, endogenous accumulation of K&H

• Low K stock & TFP in developing caused by not exploiting LCA

• Either cant exploit or not enough access to K market to exploit

Marshallian externalities (ME) model - Harrison & Rodriguez-clare (2010) - Dynamic externalities problem

Model is static not dynamic

With international knowledge spillovers we have to add conditions for specialisation transition from 1 → 2

• took China 20-30yrs to realise gains

2 needs large externalities + improvement in productivity at fast pace

• Faster change = more benefits & shorter protection

• Protection losses < discounted gains

Marshallian externalities (ME) model - Harrison & Rodriguez-clare (2010) - Dynamic externalities problem & policy

Policy needs to shift resources quickly

OR a large enough externality underlying to get to new equilibrium quickly naturally

Marshallian externalities (ME) model - Harrison & Rodriguez-clare (2010) - Exceptionality

Does a policy to achieve LCA pass Mill test

• if all economies protect some industry to achieve LCA then not optimal - even with productivity gains

• Never reach frontier as efficient for producers to stop producing before CA level (p < p*)

Protection only passes Mill test only if nation has LCA in protected sector

• China has LCA as largest economy of L in Manu

• Realised the gains so other similar nation (india) cant overturn its realisation

• India may have own LCA in tech but needs exceptionality to force switch in specialisation