8. Multiple Regression

What does change in a multiple regression compared with other types?

• we build a model to explain the variance using a linear equation

• we test how well the variability of the scores is explained by the model (R² and significance of F)

• usual assumptions apply inc. Homoscedasticity and normally distributed residuals

What are the features new in multiple regression compared with other types?

• model built using more than one predictor

• examine how much each predictor contributes to predicting the variability of the outcome measure (forced entry and hierarchical regression)

• compare different models predicting the same outcome (hierarchical regression)

• new checks on the data for assumptions and issues

What is the difference between R² and adjusted R²?

• R² tells us the estimate for our sample. Will be an overestimate of the real R² in the population

• Adjusted R² is an estimate for the population. Adjusted down to allow for the overestimation of R². Better reflection of the real R²

• the adjustment relates to sample size (bigger sample = less need for adjustment

What determines the degrees of freedom for the regression?

number of predictors (k)

What is the role of b values in multiple regression?

• we can get individual bs for each of our predictors

• they are the estimate of the contribution while controlling for the other variables

• estimate of the individual contribution of each predictor

What makes us the equation in multiple regression?

• we have a number of predictors to add to the equation

• there is still one intercept b₀

• however, there is more than one predictor

  

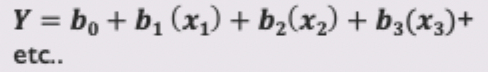
What are the 3 questions we can ask in multiple regression?

• How much of the variance in wellbeing does the overall model with the five predictors accounts for? (similar to simple)

• Do all the predictors contribute to the model?

• How do all the predictors contribute to the model? Can we tease apart the contribution of individual predictors?

Why do we need beta weights in multiple regression?

• Normal bs are affected by the distribution and type of score. Can use them in equations but can’t compare them esp. if they are different measures (IQ vs Age vs GPA)

• So we standardise. Standardised score is simply the number of SDs from the mean of the scores.

• We can then compare the contribution of each variable to the outcome, in terms of standard deviations.

What does the beta weight 0.594 show?

As our predictor increases by one standard deviation, the outcome increases by 0.594 of a standard deviation

What does the beta weight of -0.126 show?

As the predictor increases by one standard deviation, the outcome decreases by 0.126

What does testing each regression coefficient (b) in multiple regression tell us?

Whether each predictor contributes uniquely to explaining the outcome, after controlling for other predictors.

What statistical test is used to determine if a regression coefficient is significantly different from zero?

A t-test

What does it mean if a predictor is “significant” in a multiple regression model?

The predictor has a statistically significant unique effect on the dependent variable (p < .05).

What does the 95% confidence interval for a regression coefficient represent?

A range of values within which the true population coefficient is likely to fall.

How do you know from the confidence interval whether a predictor is significant?

If the 95% CI does not include zero, the predictor is significant.

This is directly linked to the t-test:

• If the CI does not include 0, the coefficient is significantly different from zero → predictor is significant

• If the CI does include 0, then zero is a plausible value → predictor is not significant

This is because CI-based significance testing aligns with t-tests at the same confidence level.

How come correlations show significant relationships between almost all big 5 factors but regression only shows that extraversion and conscientiousness are significant?

• the regression analysis controls for the other variables when estimating significance and importance

• the b_n and beta’s are better estimates of the contribution of individual predictors

• you can’t really trust your correlations, they are just an estimate of the two variables relationship without the other variables taken into consideration

How can we introduce categorical variables into regression?

• Dummy coding using 1s and 0s

• e.g. a two-level variable (gender) could be coded 0 for female and 1 for male

• a way to introduce more levels

• the variable is then entered in as you would a non-dummy variable

What does it mean if the b/beta value is positive in the Dummy variables output?

the category coded as 1 is higher in the outcome variable than the category coded as 0

What does it mean if the b/beta value is negative in the Dummy variables output?

The category coded as 0 is higher in the outcome variable

What are the usual assumptions that also apply for multiple regression?

• variable type: outcome must be continuous (predictors can be continuous or discrete)

• non-zero variance

• independence

• linearity

• homoscedasticity

• normally distributed errors

• check for outliers and influential cases

What is multicollinearity?

• multicollinearity exists when predictors are highly correlated with eachother

• if predictors are highly correlates it’s difficult to separate them. All measuring similar thing

• this assumption can be checked with collinearity diagnostics

How can multicollinearity affect findings?

• can undermine your findings

• b can be unstable (vary from sample to sample)

• difficult to say which predictor is important

• less likely to find a result if you have multicollinearity

What can we look for in output to determine multicollinearity?

• the VIF is a measure of each predictor’s relationship with other predictors - we want this to be low: anything close to 10 is an issue

• tolerance is 1 divided by the VIF, should be above 0.2

How do we check for outliers and influential cases?

• check for high standardised residuals: only about 5% should be over 2 SD

• Cook’s distance: measure of influence of each case on the model. most if not all cook’s distances should be below 1

What can we do if we violate the assumptions for multiple regression?

• Robust regression (regression without the assumptions)

• Bootstrapping: a method of finding results and their significance that doesn’t rely on underlying distributions, relies on “resampling”

• can be used in regression to derive both the coefficients and the associated tests of significance

Why might we use hierarchical regression?

• as a different way to introduce variables in the analysis

How do we perform hierarchical regression?

We add the variables into the equation in steps

1. We add the control variable in first. Examine the R² and its significance.

2. Then add the variable we are interested in and run the analysis again

3. This gives us two models

We are interested in the change of predictive power from Model 1 to 2

How can we compare between models in hierarchical regression?

The F ratio change compares the models and tells us there is a significant improvement in variance explained in model 2

How is F change calculated?

• (SSreg model 2) - (SSreg Model 1)

• divided by df of change

• divided by MS residual of model 2