10 Lesson 1: Discrete Random Variables, The Discrete Uniform Distribution, and The Binomial Distribution

What is a random variable?

A random variable is unpredictable and represents an outcome or value that can't be foreseen in advance.

What is a discrete random variable?

It can take on a countable number of outcomes which have a specific probability.

Examples: coin tosses and dice rolls

What are the properties of Probability Distributions?

* Probability values range between 0 and 1.
* ∑p(x) (sum of probabilities) equals 1.

What does P(X=x) express?

* Expresses the probability that a random variable X takes on a specific value x.
* p(x) = 0 for impossible values.
* p(x) > 0 for possible values.
* p(x) = 1 for the only possible outcome.
* Remember: 0 ≤ p(x) ≤ 1
* X is the random variable and x represents the different values it can take.

Define a continuous random variable

A random variable that has an infinite number of possible outcomes and no specific probabilities attached to individual outcomes.

What is a Probability Density Function (PDF)

Is the function associated to continuous random variables denoted by f(x). It determines the probability of outcomes within a specified range.

How can we calculate the probability under the PDF

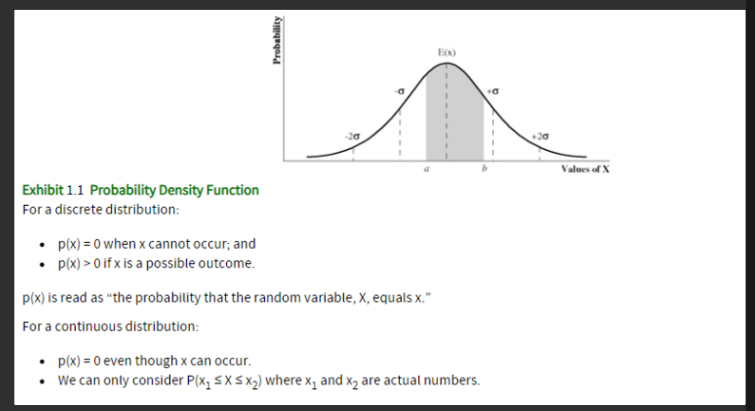
Probability is calculated as the area under the pdf curve.

What is a Cumulative Distribution Function (CDF)

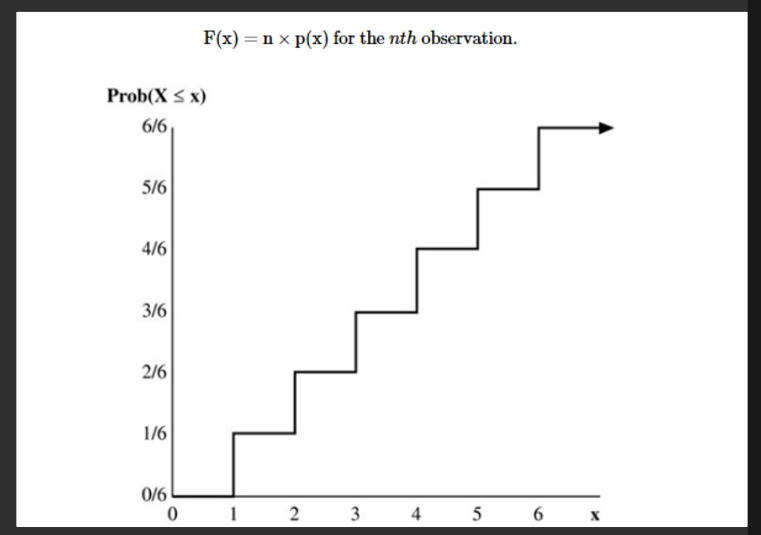
A CDF, also called a distribution function, expresses the probability that a random variable, X, will have a value less than or equal to a specific value, x. It is represented as F(x) = P(X ≤ x).

What is the purpose of the CDF

* To provide a comprehensive view of the probability distribution of a random variable.
* Helps in understanding how likely it is for the random variable to take on values within a specified range.

Define a Discrete Uniform Distribution

A discrete uniform distribution is one in which the probability of each of the possible outcomes is the same.

Define a continuous uniform distribution U(a,b)

A continuous uniform distribution is described by a lower limit, *a*, and an upper limit, b. These limits serve as the parameters of the distribution.

What is the probability of taking values outside a and b in a continuous uniform distribution?

The probability of the random variable taking on any set of values outside the parameters, a and b, equals zero.

* P(X

What is the probability of taking values that falls between x1 and x2 that both lie within the range, *a* to *b* in a continuous uniform distribution?

P(x1≤X≤x2)=(x2−x1)/(b−a)

What are Bernoulli Trials?

They are experiments with only two outcomes: success and failure. Remember that the outcome are mutually exclusive and collectively exhaustive.

What is a Bernoulli Distribution?

Describes the number of successes “X” in “n” independent Bernoulli trials.

Denoted as X ∼ B(n, p) → “X follows a binomial distribution with n trials and probability of success p.”

What are the main assumptions for a Binomial Distribution?

* Probability of success, p, is constant for all trials.
* Trials are independent; the outcome of one trial doesn't affect another.

State the formula for the probability of “x” successes in a Binomial Distribution?

How do we calculate the mean (expected value) and the variance of a random variable that follows a Binomial Distribution?

E(X)=ux=p\*n

Variance=n\*p\*(1-p)

How can we asses the skewness of a Binomial Distribution?

* If the probability of success is 0.50, the binomial distribution is symmetric.
* If the probability of success is less than 0.50, the binomial distribution is skewed to the right.
* If the probability of success is more than 0.50, the binomial distribution is skewed to the left.

How can we track errors in a portfolio returns?

Tracking error is a measure of how closely a portfolio's returns match the returns of the index to which it is benchmarked