Quiz Chapter 14 - Twee gemiddeldes vergelijken (MD 6)

Stel een ervaren bedrijf heeft 2 nieuwe designs gemaakt voor hun nieuwe webshop en wil weten of er voor hogere bedragen aangekocht wordt via 1 van de 2 webshop designs. Men besluit dit via steekproeven te onderzoeken en hiervoor worden 200 klanten aselect aan de 2 designs toegewezen. We weten dat de varianties van de aankoopbedragen in de populatie gelijk zijn voor de 2 webshop designs uit eerdere gelijkaardige gerandomiseerde experimenten.

Welke toets(en) kun je uitvoeren?

 

t-toets voor 2 steekproeven of gepoolde t-toets voor 2 steekproeven

Which of the following is not an assumption and/or condition for the paired t-test?

 

All of these.

 

Independent Groups Assumption

 

Paired Data Assumption

 

Randomization Condition

 

Nearly Normal Condition

 

Independent Groups Assumption

The transport authority “Transport for London” operates a public bike sharing-scheme that consists of 750 docking stations and 11,500 bikes. The bikes are available 24/7, 365 days a year and allow citizens and visitors to get around in London quickly and easily.

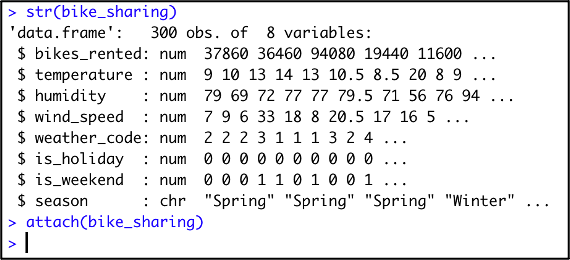
Transport for London has collected a dataset that contains the number of bikes that were rented for a random selection of 300 days from the past 5 years. Besides the number of bikes rented (bikes_rented), the dataset also contains information on the weather (temperature, wind_speed, humidity, weather_code) and type of day (is_holiday, is_weekend, season). This dataset is already loaded into R as a dataframe called “bike_sharing”. The following R console output is given:

Transport for London now wants to test with 95% confidence whether the average number of bikes that are rented on a windy day (this means a wind speed of 20 km/h or more) is significantly higher compared to the other days. Which of the following R code statements can be used to perform this test correctly?

t.test(bikes_rented[wind_speed >= 20], bikes_rented[wind_speed < 20], alternative = "greater", conf.level = .95)

Een bedrijf brengt 2 nieuwe fruitsappen op de markt en wil weten of het ene fruitsap beter in de smaak valt dan het andere bij kinderen. 2 klassen uit het derde leerjaar uit 2 verschillende scholen worden geselecteerd (elk 20 kinderen) en 1 klas geeft men fruitsap A en de andere klas fruitsap B. Ieder kind mag een score geven van 1-10. De gemiddelde smaakscore van beide fruitsappen worden vergeleken. Is hier voldaan aan de conditie van randomisatie?

 

bediscussieerbaar: je zou de randomisatie kunnen verbeteren door het uitdelen van de 2 fruitsappen niet per klas te doen, maar per kind

Welke uitspraak omtrent de geschatte effectgrootte bij de t-toets voor 2 steekproeven met H₀: µ1 - µ2 = 0 is juist?

De geschatte effectgrootte bij de t-toets voor 2 steekproeven…

 

geeft het werkelijke verschil weer tussen de populatiegemiddeldes van een kwantitatieve variabele voor 2 onafhankelijke groepen

fout

Welke uitspraak omtrent de geschatte effectgrootte bij de t-toets voor 2 steekproeven met H₀: µ1 - µ2 = 0 is juist?

De geschatte effectgrootte bij de t-toets voor 2 steekproeven…

 

geeft een schatting weer van het verschil tussen de populatiegemiddeldes van een kwantitatieve variabele voor 2 gepaarde groepen

fout

Welke uitspraak omtrent de geschatte effectgrootte bij de t-toets voor 2 steekproeven met H₀: µ1 - µ2 = 0 is juist?

De geschatte effectgrootte bij de t-toets voor 2 steekproeven…

 

geeft een schatting weer van het verschil tussen de populatiegemiddeldes van een kwantitatieve variabele voor 2 onafhankelijke groepen

juist

Welke uitspraak omtrent de geschatte effectgrootte bij de t-toets voor 2 steekproeven met H₀: µ1 - µ2 = 0 is juist?

De geschatte effectgrootte bij de t-toets voor 2 steekproeven…

 

geeft een schatting weer van het verschil tussen de steekproefgemiddeldes van een kwantitatieve variabele voor 2 onafhankelijke groepen

fout

Data were collected on annual personal time (in hours) taken by a random sample of 16 women and 7 men employed by a medium sized company. The women took an average of 24.75 hours of personal time per year with a standard deviation of 2.84 hours. The men took an average of 21.89 hours of personal time per year with a standard deviation of 3.29 hours. The standard error of the sampling distribution for the difference between the two means is

1.43

Een professionele tomatenboer, boer Teun, wil een schatting maken van het verschil in gemiddeld gewicht tussen zijn tomaten en de tomaten van Frans, die als hobby tomaten kweekt in zijn tuin. Teun neemt een steekproef van 56 tomaten, met een gemiddeld gewicht van 120 gram en een standaardafwijking van 20 gram. Frans neemt een steekproef van 20 tomaten, met een gemiddeld gewicht van 128 gram en een standaardafwijking van 22 gram. Geef een 95% betrouwbaarheidsinterval voor het verschil in gemiddeld gewicht tussen de tomaten van boer Teun en de tomaten van Frans (y¯Teun−y¯Frans).

 

Het 95% betrouwbaarheidsinterval is [-19.4190 ; 3.4190] dus we hebben niet genoeg bewijs om te zeggen dat het gemiddelde gewicht van de tomaten van boer Teun verschilt van het gemiddelde gewicht van de tomaten van Frans, bij significantieniveau van 5%.

Data were collected on annual personal time (in hours) taken by a random sample of 16 women (group 1) and 7 men (group 2) employed by a medium sized company. The women took an average of 24.75 hours of personal time per year with a standard deviation of 2.84 hours. The men took an average of 21.89 hours of personal time per year with a standard deviation of 3.29 hours. The Human Resources Department believes that women tend to take more personal time than men because they tend to be the primary child care givers in the family. The correct null and alternative hypotheses to test this belief are

H₀: μ₁ - μ₂ = 0 and H_A: μ₁ - μ₂ > 0.

An army depot that overhauls ground mobile radar systems is interested in improving its processes. One problem involves troubleshooting a particular component that has a high failure rate after it has been repaired and reinstalled in the system. The shop floor supervisor believes that having standard work procedures in place will reduce the time required for troubleshooting this component. Time (in minutes) required troubleshooting this component without and with the standard work procedure is recorded for a sample of 19 employees. In order to determine if having a standard work procedure in place reduces troubleshooting time, they should use

 

a one-tailed paired t-test.

juist fout

 

De Bijna-Normaal conditie test je voor elk type t-toets op dezelfde manier: de kwantitatieve variabele in de steekproef moet unimodaal en symmetrisch verdeeld zijn

fout

juist fout

 

De bijna-Normaal conditie test je voor de gepaarde t-toets als volgt: de verschillen van de kwantitatieve variabele berekend voor iedere paar moeten unimodaal en symmetrisch verdeeld zijn

juist

juist fout

 

De bijna-Normaal conditie test je voor de gepoolde t-toets als volgt: de verschillen van de kwantitatieve variabele berekend voor iedere paar moeten unimodaal en symmetrisch verdeeld zijn

fout

juist fout

 

De bijna-Normaal conditie test je voor de gepaarde t-toets als volgt: de kwantitatieve variabele in de 2 steekproeven apart moet unimodaal en symmetrisch verdeeld zijn

fout

Data were collected on annual personal time (in hours) taken by a random sample of 16 women and 7 men employed by a medium sized company. The women took an average of 24.75 hours of personal time per year with a standard deviation of 2.84 hours. The men took an average of 21.89 hours of personal time per year with a standard deviation of 3.29 hours. The Human Resources Department believes that women tend to take more personal time than men because they tend to be the primary child care givers in the family. The t-test for two means is appropriate in this situation because

 

women and men are independent samples.

A consumer group was interested in comparing the operating time of cordless toothbrushes manufactured by two different companies. Group members took a random sample of 18 toothbrushes from Company A and 15 from Company B. Each was charged overnight and the number of hours of use before needing to be recharged was recorded. Company A toothbrushes operated for an average of 119.7 hours with a standard deviation of 1.74 hours; Company B toothbrushes operated for an average of 120.6 hours with a standard deviation of 1.72 hours. The 90% confidence interval is (-1.93, 0.13). The correct interpretation is

 

We are 90% confident that, on average, the toothbrushes from Company B operate longer before needing to be recharged than the toothbrushes from Company A.

 

None of these.

 

We are 90% confident that, on average, the toothbrushes from Company A operate longer before needing to be recharged than the toothbrushes from Company B.

 

We are 90% confident that, on average, there is no difference in operating hours between toothbrushes from Company A compared to those from Company B.

 

We are 90% confident that, on average, there is a difference in operating hours between toothbrushes from Company A compared to those from Company B.

 

We are 90% confident that, on average, there is no difference in operating hours between toothbrushes from Company A compared to those from Company B.

We willen het gemiddelde vergelijken tussen twee populaties A en B. Hiervoor voeren we de two-sample t-test uit op twee steekproeven a en b, een uit elke populatie. We krijgen volgende output in RStudio. 

Duid de juiste uitspraak aan, gebaseerd op deze output.

Het verschil tussen de steekproefgemiddeldes is onbekend maar we weten met 95% zekerheid dat het ligt tussen -2.929419 en 3.150642

 

Het verschil tussen de steekproefgemiddeldes is te wijten aan steekproefvariabiliteit

 

We voeren een eenzijdige hypothesetest uit

 

Het gemiddelde in populatie A is significant hoger dan het gemiddelde in populatie B

 

Het verschil tussen de steekproefgemiddeldes is te wijten aan steekproefvariabiliteit

An army depot that overhauls ground mobile radar systems is interested in improving its processes. One problem involves troubleshooting a particular component that has a high failure rate after it has been repaired and reinstalled in the system. The shop floor supervisor believes that having standard work procedures in place will reduce the time required for troubleshooting this component. Time (in minutes) required troubleshooting this component without and with the standard work procedure is recorded for a sample of 19 employees. Assuming that we define our differences as Time without standard work procedure - Time with standard work procedure, the correct alternative hypothesis is

 

μ_d > 0.

Data were collected on annual personal time (in hours) taken by a random sample of 16 women (group 1) and 7 men (group 2) employed by a medium sized company. The women took an average of 24.75 hours of personal time per year with a standard deviation of 2.84 hours. The men took an average of 21.89 hours of personal time per year with a standard deviation of 3.29 hours. The Human Resources Department believes that women tend to take more personal time than men because they tend to be the primary child care givers in the family. The results of the test are t = 2.02 with an associated P-value of 0.0352. The correct conclusion at α = 0.05 is to

I. reject the null hypothesis.
II. fail to reject the null hypothesis.
III. conclude that women take a higher average number of hours of personal time per year compared to men.

 

Both I and III

Onderzoeksvraag: valt een nieuw product beter in de smaak bij kinderen of volwassenen? Experimentele opzet: de deelnemers bestaan uit telkens 1 ouder met eigen kind en je laat hen beiden een product proeven. Je noteert de score die ze elk geven voor het product (score 1-10). De totale steekproef bevat 10 ouders en 10 kinderen. De toets bestaat erin na te gaan of kinderen en ouders gemiddeld een verschillende score geven. 
Vraag: is deze data gepaard of ongepaard?

gepaard

Stel dat een winkel wil nagaan of de smaak van een product anders beoordeeld wordt bij kinderen dan bij volwassenen. Ze willen dit aan de hand van een steekproef nagaan en vragen telkens aan 1 ouder die met zijn/haar kind naar de winkel komt of beiden het product kunnen proeven en vragen om een score te geven van 1-10. In totaal worden 16 ouder-kind paren bevraagd. Uit de steekproef komen volgende gegevens:

Voer de juiste hypothesetest uit om de onderzoeksvraag te beantwoorden en duid de juiste conclusie aan. Werk op significantieniveau 0.01.

 

Er is geen significant verschil tussen de score van de ouders en van hun kinderen.

Een bedrijf brengt 2 nieuwe fruitsappen op de markt en wil weten of het ene fruitsap beter in de smaak valt dan het andere bij kinderen. 2 klassen uit het derde leerjaar uit 2 verschillende scholen worden geselecteerd (elk 20 kinderen) en de ene klas geeft men fruitsap A en de andere fruitsap B. Ieder kind mag een score geven van 1-10. De gemiddelde score van beide fruitsappen worden vergeleken. Zijn de 2 groepen onafhankelijk?

ja

Glaucoom is een veel voorkomende oogziekte, die in de meeste gevallen gepaard gaat met een te hoge druk binnen in het oog. Cafeïne verlicht de druk binnen het oog. Daarom wordt er een experimenteel onderzoek opgezet dat test of langdurig gebruik van cafeïne de oogdruk permanent kan verlichten. 40 proefpersonen doen mee aan dit onderzoek. 22 van hen vormen de controlegroep en zullen geen cafeïne krijgen. 18 van hen zullen wel cafeïne krijgen. Na de behandeling is bij de controlegroep de gemiddelde druk in het oog 16 mmHg (kwikdruk) met een standaardafwijking van 5 mmHg. Bij de groep die cafeïne heeft gekregen is de gemiddelde oogdruk 14 mmHg met een standaardafwijking van 4 mmHg. Stel een hypothesetest op die test of langdurig gebruik van cafeïne de oogdruk kan verlagen. Werk op significantieniveau 0.1.

 

De P-waarde is 0.08402 en dus besluiten we dat cafeïne de oogdruk kan verlagen

An army depot that overhauls ground mobile radar systems is interested in improving its processes. One problem involves troubleshooting a particular component that has a high failure rate after it has been repaired and reinstalled in the system. The shop floor supervisor believes that having standard work procedures in place will reduce the time required for troubleshooting this component. Time (in minutes) required troubleshooting this component without and with the standard work procedure is recorded for a sample of 19 employees. The P-value associated with the calculated test statistic is < 0.001. At α = 0.05, the correct conclusion is to

I. reject the null hypothesis.
II. fail to reject the null hypothesis.
II. conclude that having standard work procedures in place reduces troubleshooting time for this component.

 

Both I and III

De Vlaamse Wiskunde Olympiade (VWO) is een vragenlijst van 30 meerkeuzevragen waarbij inzicht nodig is om en hoge score te behalen. Je wil testen of de leerlingen van school A betere scores halen dan de leerlingen van school B. Van school A neem je hiervoor een steekproef van 22 leerlingen uit de groep deelnemers van de VWO. Hier vind je een gemiddelde score van 92.5 met een standaarddeviatie van 6. Van school B neem je een steekproef van 18 deelnemers. Hier vind je een gemiddelde score van 88 met een standaarddeviatie van 8. Voer een gepaste hypothesetest uit om de onderzoeksvraag te beantwoorden en duid de juiste conclusie aan die je kan halen uit deze hypothesetest. Werk op significantieniveau 0.05.

 

School A scoorde significant beter dan school B

An army depot that overhauls ground mobile radar systems is interested in improving its processes. One problem involves troubleshooting a particular component that has a high failure rate after it has been repaired and reinstalled in the system. The shop floor supervisor believes that having standard work procedures in place will reduce the time required for troubleshooting this component. Time (in minutes) required troubleshooting this component without and with the standard work procedure is recorded for a sample of 19 employees. The standard error of the mean difference is

Without Standard Work Procedure	With Standard Work Procedure	Difference Without - With
142	119	23
144	118	26
153	126	27
148	119	29
146	121	25
149	125	24
138	116	22
145	120	25
153	124	29
160	138	22
163	135	28
170	144	26
169	142	27
151	128	23
152	131	21
167	141	26
164	140	24
165	140	25
163	138	25

 

0.529

The transport authority “Transport for London” operates a public bike sharing-scheme that consists of 750 docking stations and 11,500 bikes. The bikes are available 24/7, 365 days a year and allow citizens and visitors to get around in London quickly and easily.

Transport for London has collected a dataset that contains the number of bikes that were rented for a random selection of 300 days from the past 5 years. Besides the number of bikes rented (bikes_rented), the dataset also contains information on the weather (temperature, wind_speed, humidity, weather_code) and type of day (is_holiday, is_weekend, season). This dataset is already loaded into R as a dataframe called “bike_sharing”. The following R console output is given:

  

Transport for London now wants to test with 95% confidence whether the average number of bikes that are rented on a windy day (this means a wind speed of 20 km/h or more) is significantly lower compared to the other days. Which of the following R code statements can be used to perform this test correctly?

t.test(bikes_rented[wind_speed >= 20], bikes_rented[wind_speed < 20], paired = TRUE, conf.level = .95)

 

t.test(bikes_rented[wind_speed >= 20], bikes_rented[wind_speed < 20], alternative = "greater", conf.level = .95)

 

t.test(wind_speed[bikes_rented >= 20], wind_speed[bikes_rented < 20], paired = TRUE, conf.level = .95)

 

t.test(wind_speed[bikes_rented >= 20], wind_speed[bikes_rented < 20], alternative = "greater", conf.level = .95)

t.test(bikes_rented[wind_speed >= 20], bikes_rented[wind_speed < 20], alternative = "less", conf.level = .95)

juist fout

 

Indien je niet weet of de populatievarianties gelijk zijn in 2 groepen mag je geen gepoolde t-toets voor 2 steekproeven uitvoeren

juist

juist fout

 

De gepoolde t-toets en betrouwbaarheidsinterval heeft een iets hogere power en precisie indien voldaan is aan de voorwaarde van gelijke populatievarianties in de 2 groepen dan de niet-gepoolde t-toets voor 2 steekproeven

juist

juist fout

 

Indien je weet dat de populatievarianties gelijk zijn in 2 onafhankelijke groepen moet steeds een gepoolde t-toets voor 2 steekproeven uitgevoerd worden i.p.v. de niet-gepoolde t-toets voor 2 steekproeven

fout

juist fout

 

De gepaarde t-toets is mathematisch gelijk aan de t-toets voor 1 steekproef met als verschil dat er eerst een nieuwe variabele dient berekend te worden, nl. het verschil voor elk van de paren

juist

The transport authority “Transport for London” operates a public bike sharing-scheme that consists of 750 docking stations and 11,500 bikes. The bikes are available 24/7, 365 days a year and allow citizens and visitors to get around in London quickly and easily.

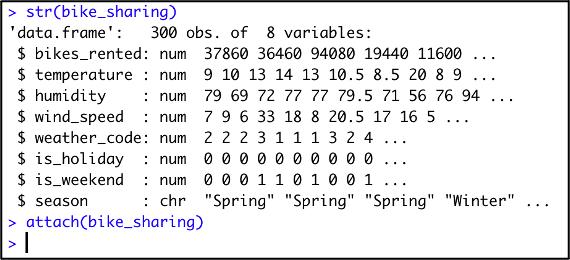
Transport for London has collected a dataset that contains the number of bikes that were rented for a random selection of 300 days from the past 5 years. Besides the number of bikes rented (bikes_rented), the dataset also contains information on the weather (temperature, wind_speed, humidity, weather_code) and type of day (is_holiday, is_weekend, season). This dataset is already loaded into R as a dataframe called “bike_sharing”. The following R console output is given:

  

Transport for London now wants to test with 95% confidence whether the average number of bikes that are rented on a windy day (this means a wind speed of 20 km/h or more) significantly differs compared to the other days. Which of the following R code statements can be used to perform this test correctly?

t.test(bikes_rented[wind_speed >= 20], bikes_rented[wind_speed < 20], conf.level = .95)