Micro Economics L8 - L14

Topics covered: Mix strategies 1 and 2, Not covered: Short and Long answers questions - look at the lecture slides

Look over the first Class experiment 

Recap the following terms: Normal Form games, Strategy, Complete information, Full rationality and common knowledge

What does iterated deletion mean

Iterated deletion is a process used in game theory to simplify a strategic game by repeatedly removing dominated strategies. A strategy is considered "dominated" if another strategy is always better for a player, regardless of what other players do. The process continues by eliminating strategies that are dominated in the new, smaller game, until no more strategies can be removed. 

Examples of Mixed strategy

Inspecting + Auditing

Military

What is a mixed strategy Nash Equilibrium in a Penalty situation 

No Nash equilibrium as presented previously.

Should involve some randomness

What is the difference between a pure strategy and Mixed strategy

What principle from Nash equilibria broadly still applies here

Eqm = Equilibrium

How would you set up for a mixed strategy equilibria 

Add probabilities in.

Randomise an equilibrium, have to be indifference in strategies. One cannot be dominate compared to the other.

Based on the example above what is the outcome of q (Probability)

The expected payoff of going right has to be equal to going left, therefore we make it equal to each other

What about P from the example above

The expected payoff of going right has to be equal to going left

What does the equilibrium mean in the example

With the probability (1/3)

What does willingness to mix with equal probability mean in order to keep the other player indifferent in equilibrium 

Explaination to willing to mix with equal probability:

Simplified Explanation of the Randomization Principle

In a mixed strategy equilibrium, the logic is:

1. Your Goal: Keep the Opponent Guessing. As a rational player, you don't want your opponent to know what you'll do next. If they could predict your move, they would always choose the action that maximizes their own payoff against yours, leaving you worse off.

2. The Method: Make the Opponent Indifferent. To make your opponent completely unpredictable (i.e., force them to randomize), you must choose your probabilities (the "mix") in such a way that every single choice they could make gives them the exact same average result.

3. The Result: Stability. Since the opponent gets the same payoff no matter which action they choose, they have no strict reason to favor one over the other. They are then willing to randomize their own moves, which is the only way for the equilibrium to be stable.

In short: You randomize your actions to keep the opponent indifferent, which in turn forces the opponent to randomize their actions, making the equilibrium stick.

Complete this example

0.3 × 0.3 = 0.09

Explanation: Player one is indifferent to whatever player 2 chooses, so we are looking at the probabilities on the first line. I will get 0, given the probability that player two selects ignore as well, and then I will get 10, given that player 2 phones the police

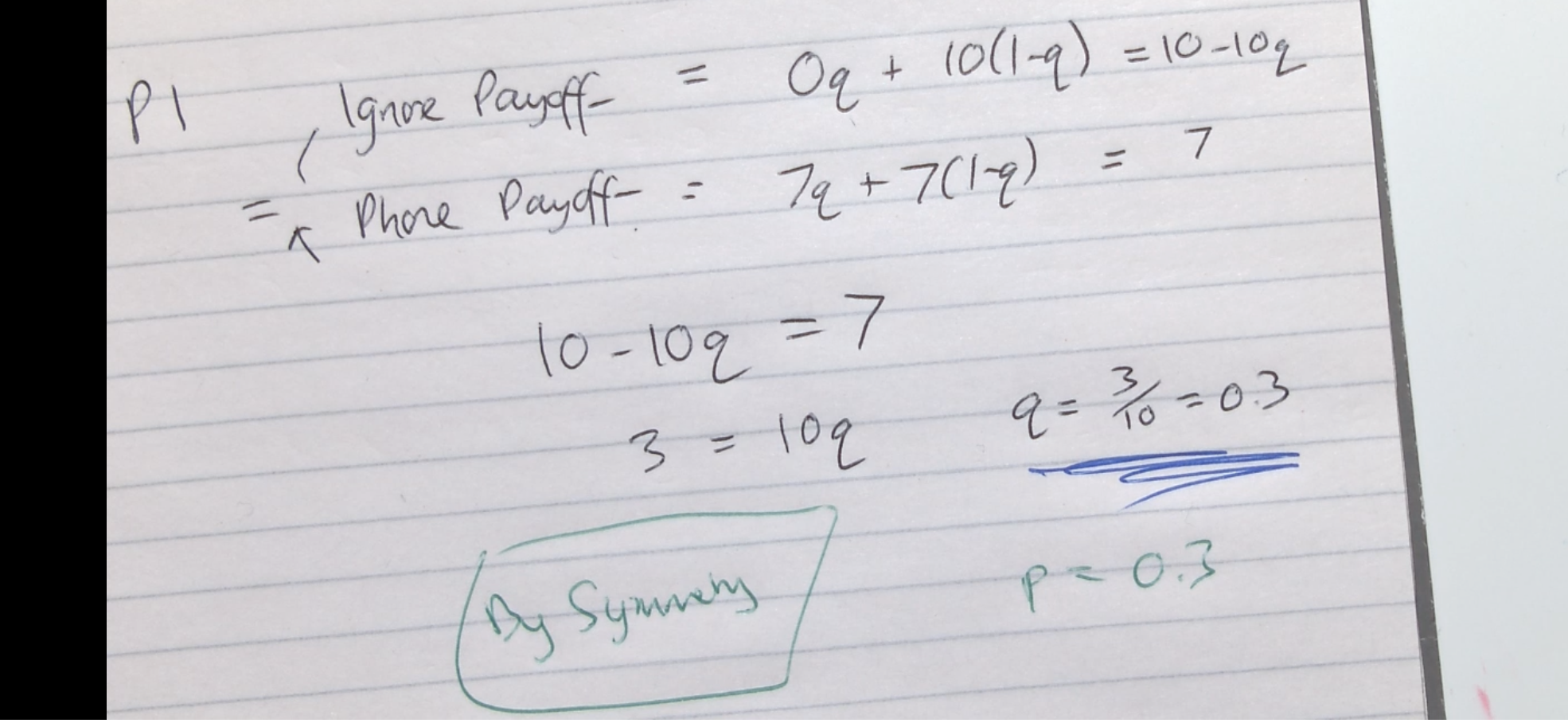
When do Mixed strategy equilibrium arise

Some cons of mixed strategy equilibrium 

Some situations where people are unpredictable, but are they random??

Situations which are indifference are very uncommon

Regret, makes it sense like it shouldn't be an equilibrium. Penalty shoot out example

 

Not good at randomising, rock paper scissors video example. If you aren't random we can take advantage of this and win, not captured in the equilibria.

Some pros of mixed strategy equilibria

Unpredictability

What are some pieces of evidence for mixed strategy equilibria

Frequently relative to that predicted

Do iteration deletion on this example

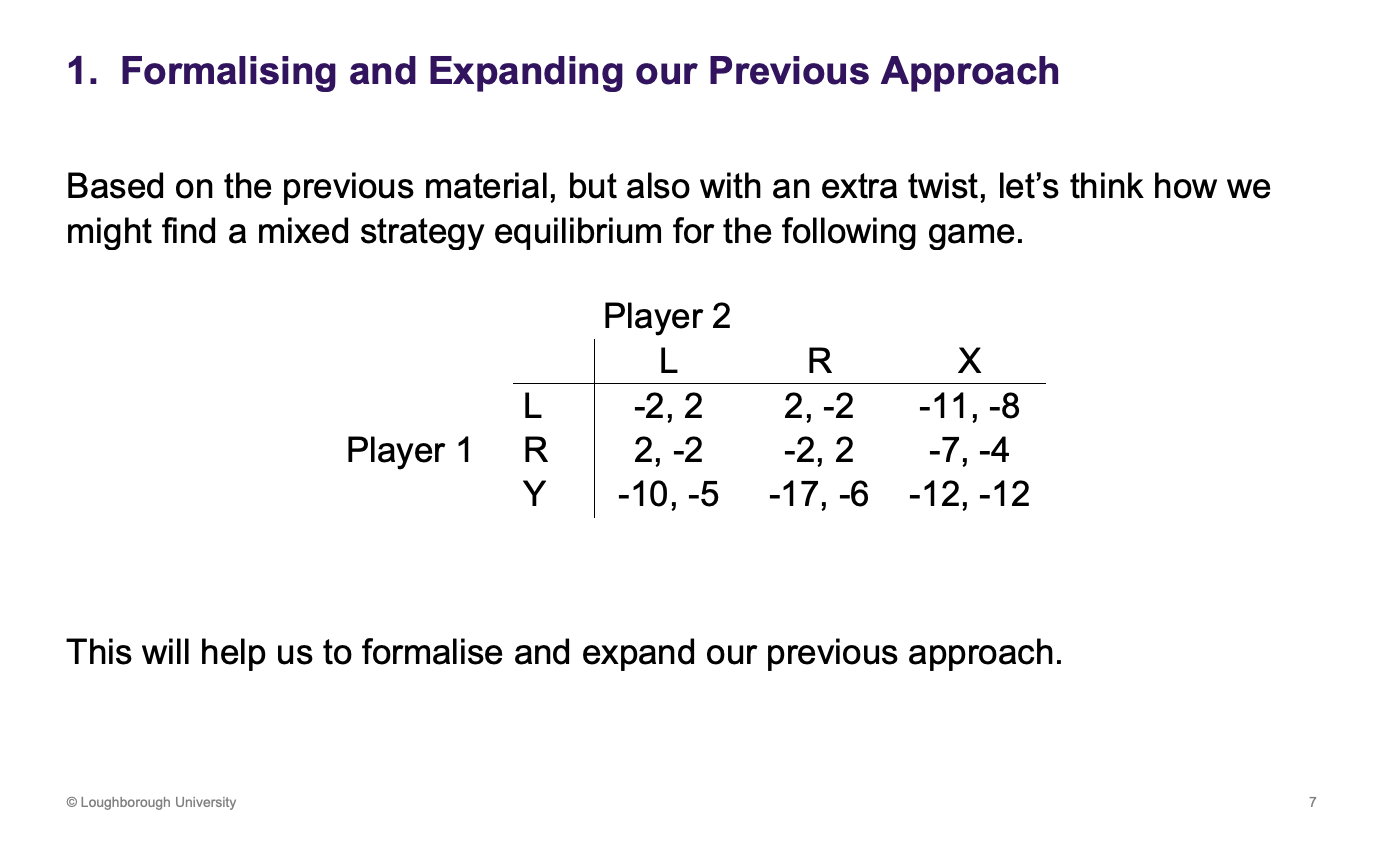
What does iteration deletion mean

Rationalizable - can be rational depending on what the other player chooses

Assess whether this example is mixed strategy

Will arise, when no pure strategy equilibrium and/or more than one pure strategy equilibrium.

Find the probability distributions of the example above

Has to be indifferent otherwise the wont be random, which is needed 

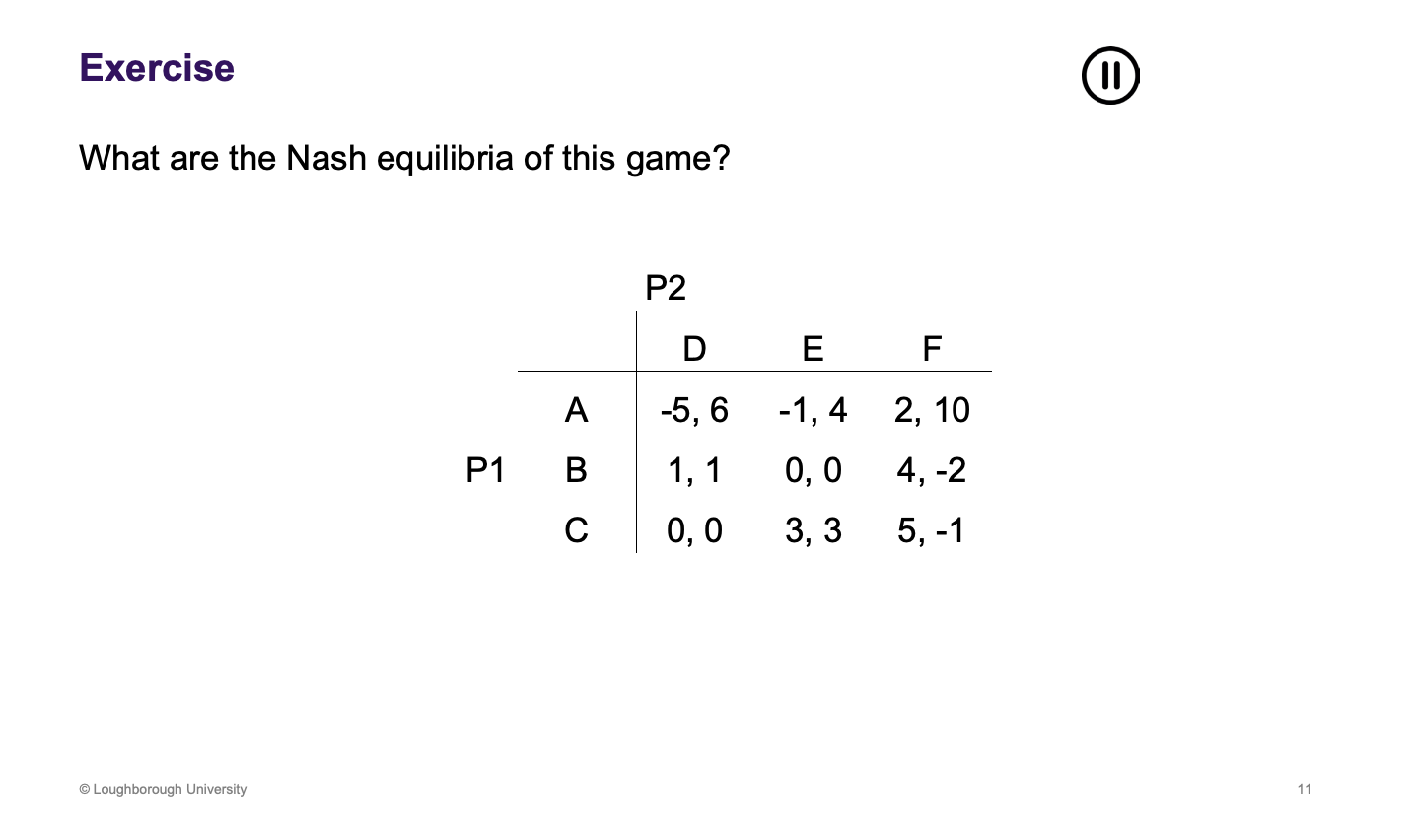
Work through this example

Answers written in the book

What are continuous strategy called

Some examples of All Pay auctions

Bidding on contracts is an example

Examples. Marketing, Football clubs, War, job applications

 

Legal Battles or Lobbying

Rewards in organisations (e.g Promotions)

What are the assumptions of a model in a continuous space

Describe the pay offs of the model

Prize is worth Z and b is the bid

How do you get to the equilibrium Step 1

Paying more than what the prize is worth - irrational

How do you get to the equilibrium Step 2a

How does the logic in step 2a apply to the class experiement

How do you get to the equilibrium Step 2b (how do you get the probability distributions)

Infinite values between 0 and V, this is why we need probability distributions rather than p and q

What is a cumulative distribution function

At 3, half the probability is less than 3 and half is above 3.

F(b) is never decreasing

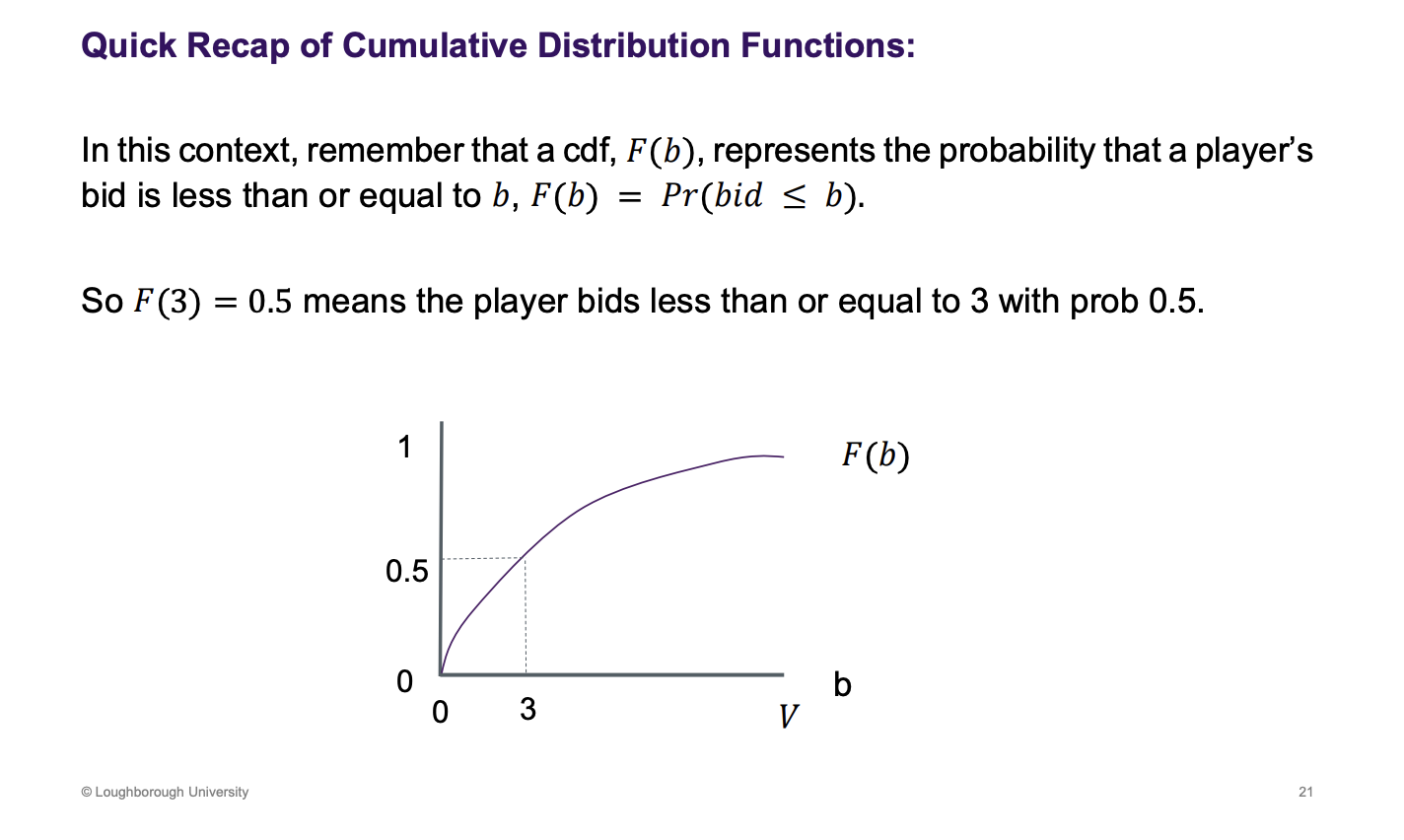
Too have a well behaved cumulative function, what assumptions must hold

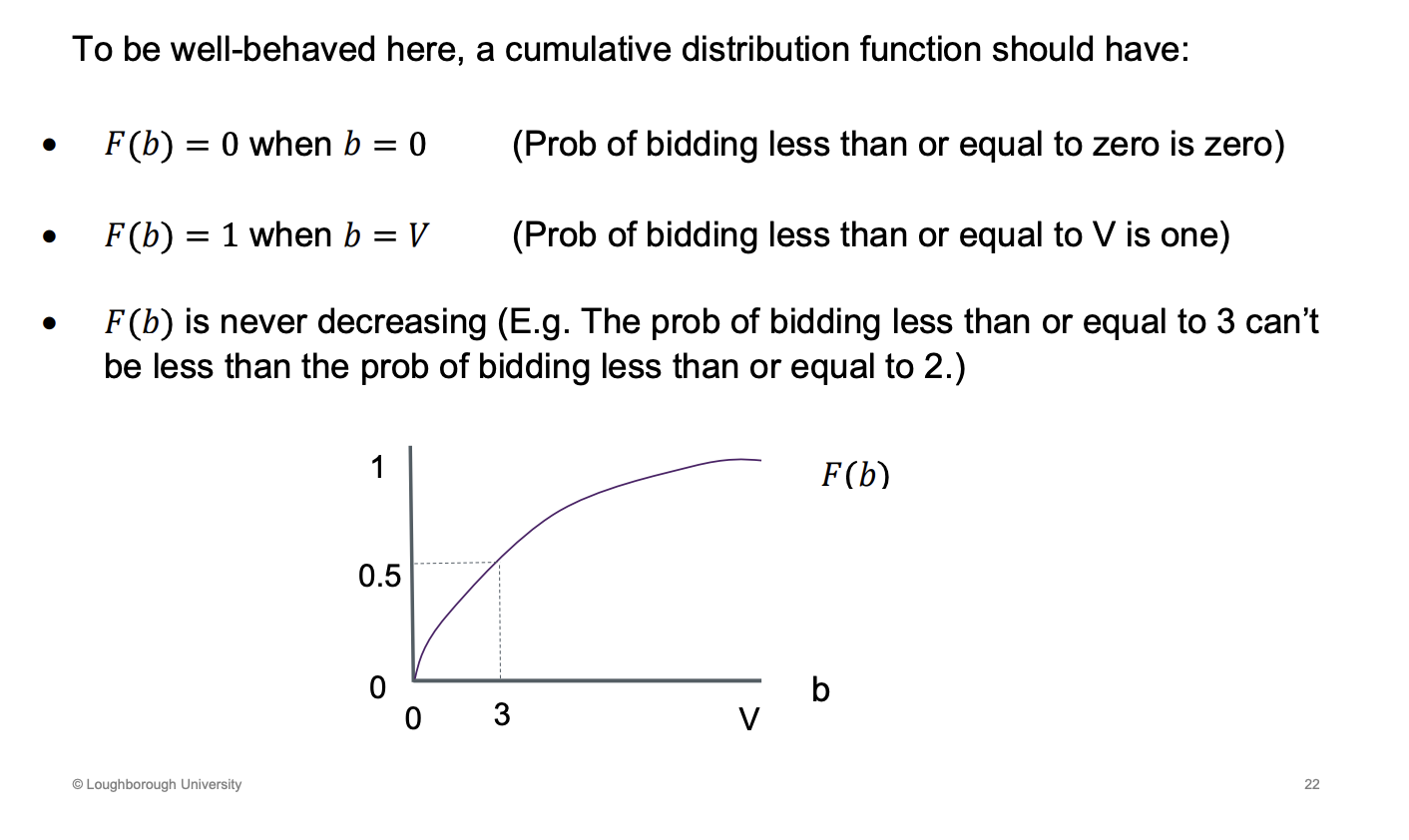
What function of b would make a player bid indifferently

Prize * probability that the other player bid the same or less than what I bid, minus the bid value

 

If you bid 0, the chance of winning is 0 and the bid is 0 so your payoff would be 0

What is the equation that connects expected payoff and bids

What is the equation which shows that there is a mixed strategy nash equilibrium 

What does the equilibrium distribution mean F(b) = (b/V) 

In eqm, equally likely to pick any bid between 0 - 10, keeps the other player in different as well

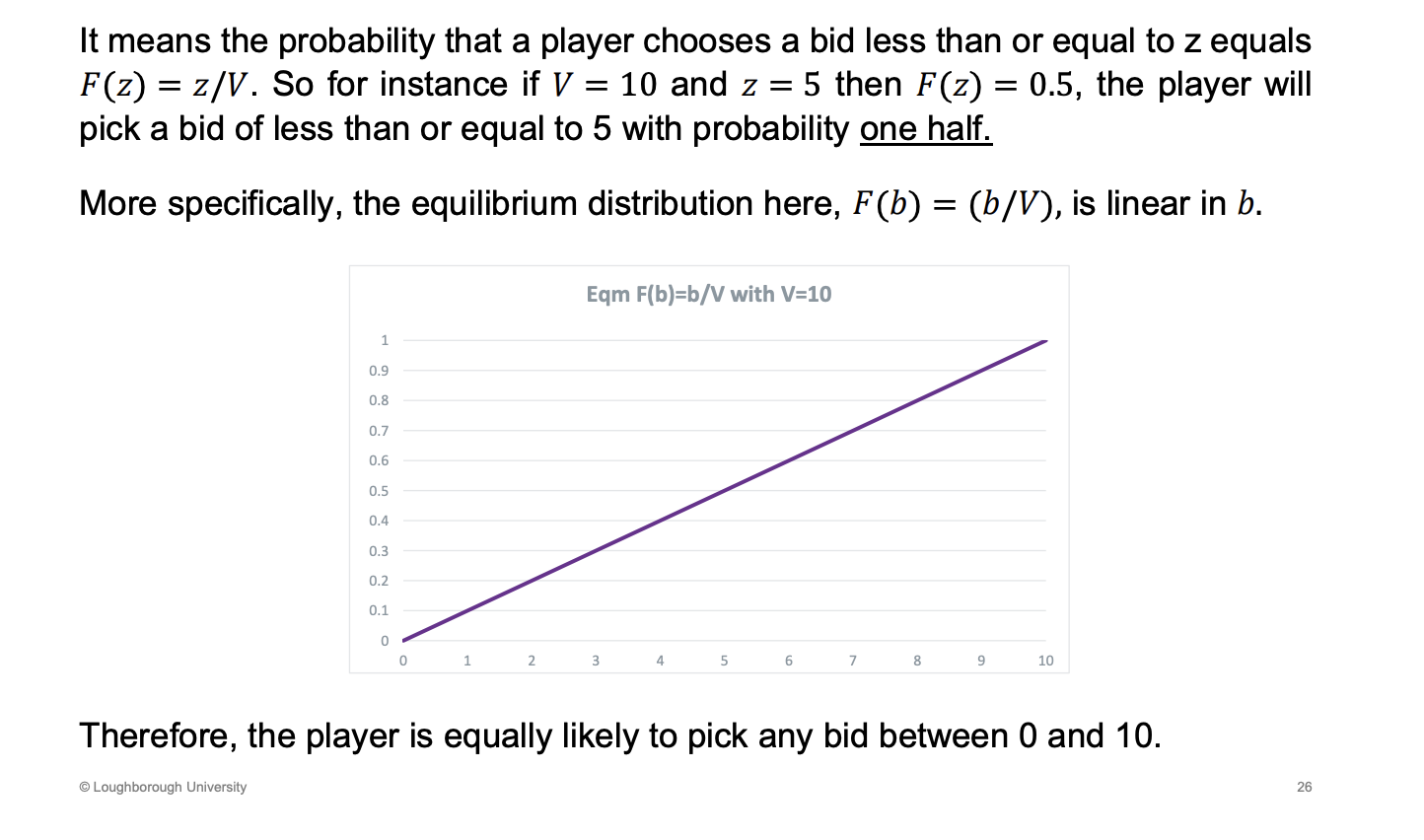
What does the all pay auction show

How can the outcome something differ to what is expected in a all pay auction

How is the equilibrium impact with more players 

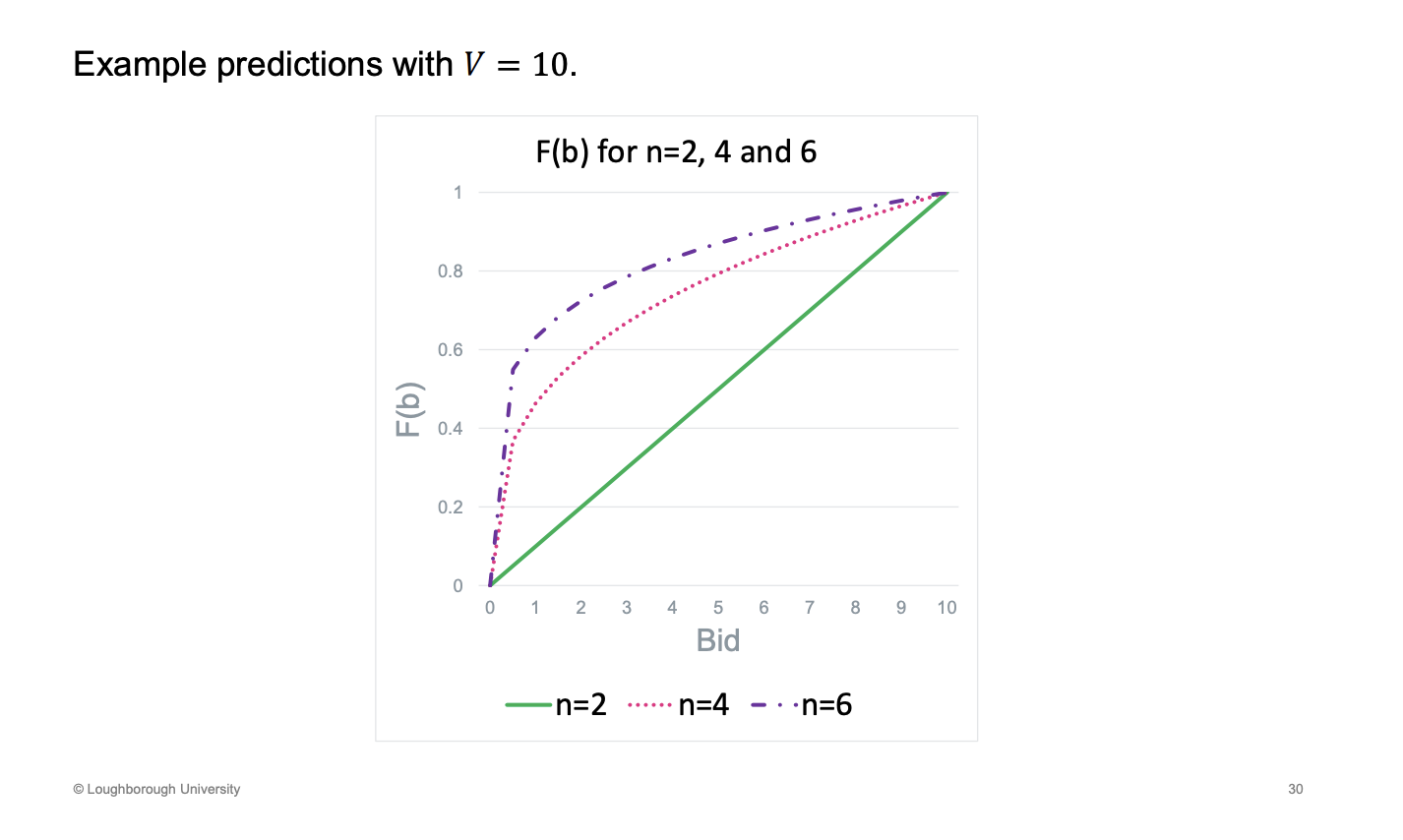
How is the equilibrium impact with more players (continued)

globalisation

What is a prime example of all pay auctions