Forschungsmethoden - Multiple Regression und Parameterschätzung

Wie lautet die allgemeine Gleichung für eine multiple Regression?

Y=β0​+β1​X1​+β2​X2​+⋯+βk​Xk​+ε

Erkläre die Parameter der multiplen Regression (Y=β0​+β1​X1​+β2​X2​+⋯+βk​Xk​+ε)

Y: abhängige Variable (Zielgröße, die wir vorhersagen wollen)

β0: Y-Achsenabschnitt

ß1, …: Regressionskoeffizienten (Einfluss jedes Prädiktors auf YYY, bei konstanten anderen Variablen)

X1, X2,…: Unabhängige Variablen (Prädiktoren)

ε: Fehlerterm (Abweichung der tatsächlichen Werte von den vorhergesagten Werten, oft „Residuen“ genannt)

Erkläre, wie eine lineare Regression geometrisch aussieht.

Eine Gerade in einem Koordinatensystem (2D)

→Die Steigung (β1) sagt uns, wie stark Y steigt oder fällt, wenn X um 1 Einheit steigt

→Der Achsenabschnitt (β0) ist der Schnittpunkt mit der Y-Achse

Erkläre, wie eine multiple Regression geometrisch aussieht.

Eine Ebene in einem 3D-Raum

→Achsen: X1, X2, Y

→β1​ und β2 bestimmen die Neigung der Ebene in Richtung von X1​ bzw. X2

→Der Fehlerterm ε ist der „Abstand“ eines Punktes (Beobachtung) von dieser Ebene​

Warum braucht man überhaupt eine Parameterschätzung?

• Ohne Parameterschätzung bleibt das Modell nur eine Formel ohne konkrete Zahlen.

• Erst mit geschätzten Parametern kann man sagen:

  „Wenn X1​ um 1 steigt, steigt Y im Mittel um 2,5 – vorausgesetzt, alle anderen Variablen bleiben konstant.“

Was sind die Passungskriterien für die Parameterschätzung? Oder anders gefragt: wie werde die Parameter geschätzt?

• Methode der kleinsten Fehlerquadrate

• Maximum Likelihood

Was ist der Unterschied zwischen Parameterschätzung und Modellpassung?

Erst schätzen wir die Parameter → dann bewerten wir, wie gut das Modell damit passt.

• Parameterschätzung:

  • Ziel: Finde die Werte der Modellparameter (β\betaβ) so, dass das Modell am besten zu den Daten passt.

  • Wie? → Optimierungsverfahren (z. B. Kleinste Fehlerquadrate oder Maximum Likelihood).

  • Ergebnis: Die optimalen Parameterwerte.

• Modellpassung:

  • Ziel: Beurteile, wie gut das Modell mit den geschätzten Parametern die Daten beschreibt.

  • Wie? → Kennzahlen wie R2 (Anteil erklärter Varianz) oder Likelihood (Wahrscheinlichkeit der Daten unter dem Modell).

  • Ergebnis: Zahl(en), die die Güte des Modells ausdrücken.

Was sind die Passungskriterien für die Modellpassung?

• Fehlerquadrate →Varianzaufklärung (rquadrat)

• Likelihood →Wahrscheinlichkeit der Daten, gegeben das parametrisierte Modell

Erkläre kurz nochmals die Passungskriterien bei Parameterschätzung und Modellpassung und wie sie zusammenhängen.

1. Parameterschätzung – „Parameter finden“

• Ziel: Werte von β bestimmen, die optimal zu den Daten passen.

• Passungskriterien:

  • Kleinste Fehlerquadrate → Minimiert Summe der quadrierten Residuen.

  • Maximum Likelihood → Maximiert Wahrscheinlichkeit der beobachteten Daten unter dem Modell.

2. Modellpassung – „Güte bewerten“

• Ziel: Prüfen, wie gut das Modell mit den geschätzten Parametern zu den Daten passt.

• Passungskriterien:

  • Fehlerquadrate → R2 = Anteil erklärter Varianz.

  • Likelihood → Wie wahrscheinlich sind die Daten unter dem geschätzten Modell?

Merksatz:

Erst optimieren (Parameterschätzung) → dann bewerten (Modellpassung).
Passungskriterien tauchen in beiden Schritten auf, aber mit unterschiedlicher Funktion.

Definiere den Begriff “Residuen”.

Residuen = Beobachteter Wert – vorhergesagter Wert

Warum wichtig?

• Residuen zeigen, was das Modell nicht geschafft hat zu erklären.

• Ihre Verteilung und Struktur sagen dir, ob deine Modellannahmen erfüllt sind.

• Bildlich

  Stell dir vor, du hast eine Punktewolke und legst eine Regressionsgerade oder -ebene hinein:

  • Jeder Punkt hat einen vertikalen Abstand zur Linie/Ebene.

  • Dieser Abstand = Residuum

Merke: Residuen = das, was nach der Vorhersage noch übrig bleibt.
Sie enthalten die „Fehler“ des Modells und sind entscheidend, um die Güte und Annahmen zu prüfen.

Wie kann ich die Modellannahme der Normalverteilung graphisch prüfen?

• Residualplot →streuen die Punkte einigermaßen normalverteilt um die vorhergesagten Werte?

• Q-Q-Plot→ entsprechen die empirischen Quantile der z-standardisierten Residuen denen der Standardnormalverteilung?

Wie sollte ein Q-Q-Plot aussehen, wenn die Daten normalverteilt sind?

 

Wenn die Daten normalverteilt sind, dann sollten die Punkte alle auf einer Gerade liegen 

→ es ist normal, dass die Plots oben und unten bisschen "ausfransen"; ist aber eine Modellverletzung; zentral ist aber, das die Punkte in der Mitte auf der Geraden liegen

Ganz allgemein: was prüft eine Modelltestung?

Prüft, ob die Modellpassung statistisch bedeutsam ist oder vielleicht nur durch Zufall entstanden ist.

Welche Methoden gibt es zur Modelltestung, die eine Signifikanzüberprüfung machen (basierend auf Fehlerquadraten)?

• F-Test

• t- Test

Welche Informationskriterien gibt es zur Modelltestung (basierend auf Likelihood)?

• Akaike Information Criterion (AIC)

• Bayesian Information Criterion (BIC)

→relativieren Vorhersagekraft an Parameterzahl →je niedriger, desto besser

→Achtung: der absolute Wert ist bedeutungslos (abhängig von jeweiligen Daten)

Was genau macht der F-Test (Signifikanzprüfung, basierend auf Fehlerquadraten)

• Nullhypothese: H0:Rquadrat=0 →Modell erklärt keine Varianz

• Bezieht sich auf: Gesamtmodell (alle Prädiktoren zusammen).

• Interpretation: Signifikanter F-Test → mindestens ein Prädiktor trägt signifikant zur Erklärung bei.

Was genau macht der t-Test (Signifikanzprüfung, basierend auf Fehlerquadraten)?

• Nullhypothese: H0:βj= → Prädiktor j hat keinen Einfluss.

• Bezieht sich auf: Einzelne Prädiktoren.

• Interpretation: Signifikanter t-Test → dieser Prädiktor hat einen signifikanten Effekt (unter Kontrolle der anderen Variablen)

Was genau macht das AIC (Informationskriterium, basierend auf Likelihood)?

Akaike Information Criterion (AIC)

• Formel: −2⋅ℓ(θ)+2k

• Idee: Balance zwischen Modellgüte (Likelihood) und Einfachheit (wenige Parameter).

• Interpretation: Je kleiner der AIC, desto besser das Modell (unter Modellen, die man vergleicht).

Was genau macht das BIC (Informationskriterium, basierend auf Likelihood)?

Bayesian Information Criterion (BIC)

• Formel: −2⋅ℓ(θ)+ln⁡(n)⋅k

• Strenger als AIC (straft mehr für viele Parameter, besonders bei großem nnn).

• Interpretation: Je kleiner der BIC, desto besser – bevorzugt einfachere Modelle bei großen Stichproben.

Wie kann ich mir all diese Tests (F-Test, t-Test, AIC, BIC) in einem Satz gut merken?

💡 Merksatz:

• F-Test = „Ist das Modell insgesamt sinnvoll?“

• t-Test = „Ist dieser eine Prädiktor wichtig?“

• AIC/BIC = „Welches Modell ist am besten, wenn ich mehrere vergleiche?“

Interpretiere die Bestandteile der Formel des AIC.

AIC

Formel:

AIC=−2⋅ℓ(θ^)+2k

• ℓ(θ)→ Log-Likelihood des Modells mit den geschätzten Parametern θ.

  • Misst, wie wahrscheinlich die Daten unter diesem Modell sind.

  • Höhere Likelihood = bessere Passung.

• −2 → Technische Umformung, damit wir ein Minimierungsproblem haben (kleiner = besser).

• k → Anzahl der geschätzten Parameter im Modell.

• 2k → Strafe für Modellkomplexität → je mehr Parameter, desto höher der Wert, desto „schlechter“ der AIC.

Interpretation:

• Guter AIC = hohe Modellpassung (große Likelihood) + wenig Parameter.

Interpretiere die Bestandteile der Formel des BIC.

BIC

Formel:

BIC=−2⋅ℓ(θ)+ln⁡(n)⋅k

• ℓ(θ) → wieder die Log-Likelihood (Passungsgüte).

• −2 → wieder: Wir wollen minimieren.

• n → Stichprobengröße.

• ln⁡(n) → Strafe für Modellkomplexität, die stärker wird, je größer die Stichprobe ist.

• k → Anzahl der geschätzten Parameter.

Interpretation:

• Guter BIC = hohe Passung + besonders starke Strafe für viele Parameter (bei großem n sehr streng).

Definiere “Population”

=Grundgesamtheit (Gesamtmenge aller Beobachtungseinheiten (N), über die Aussagen getroffen werden sollen)

Wann spricht man von einer Vollerhebung?

Wenn alle Objekte einer Population untersucht werden

Definiere “Stichprobe”

Eine Teilmenge der Population (n aus N)

Welche Gründe gibt es, “nur” eine Stichprobe zu ziehen?

• Population ist unendlich groß

• Population ist nur teilweise bekannt

• durch Art der Untersuchung würde die Population zu stark beeinträchtigt oder gar zerstört

• die Untersuchung der gesamten Population wäre zu aufwändig

Welche Arten von Repräsentativität gibt es bei einer Stichprobe?

• merkmalsspezifisch repräsentativ: die Stichprobe entspricht in für den für die Untersuchung relevanten Merkmalen der Population

• global repräsentativ: die Stichprobe entspricht in nahezu allen Merkmalen der Population.

Warum ist folgende Aussage nicht korrekt?: “je mehr Leute ich habe, desto repräsentativer ist meine Stichprobe.”

Wenn bei Stichprobenziehung relevante Merkmale nicht entsprechend der Population verteilt sind, ändern mehr Personen nichts an der fehlenden Repräsentativität →die Verzerrung wiederholt sich nur im größeren Stil

Was ist “Coverage” im Rahmen der Stichprobenziehung?

Man unterscheidet zwischen:

• angestrebter Grundgesamtheit: umfasst alle Elemente, über die Aussagen getroffen werden sollen

• Auswahlgesamtheit: umfasst alle Elemente, die eine prinzipielle Chance haben, in eine Stichprobe zu gelangen

• Inferenz-Population: wird mit einem Ziehungsverfahren tatsächlich erreicht

Welche “coverage error” können im Rahmen der Stichprobenziehung auftreten?

• undercoverage: Elemente der angestrebten Grundgesamtheit sind nicht in der Auswahlgesamtheit enthalten

• overcoverage: bestimmte Elemente haben eine höhere Wahrscheinlichkeit in die Stichprobe zu kommen oder gehören nicht zur angestrebten Grundgesamtheit

Was sind die Schritte einer einfachen Zufallsstichprobe?

Methode zum Erlangen einer repräsentativen Stichprobe:

• Alle Elemente der Population (N) müssen bekannt sein

• Es wird eine vollständige Liste dieser Elemente aufgeführt

• Aus dieser Liste werden Elemente zufällig gezogen →Stichprobe (n)

Wann spricht man von einer “einfachen Zufallsstichprobe”?

Wenn alle Elemente aus der Population (N) die gleiche Ziehungswahrscheinlichkeit haben.

Wie berechnet man bei einer einfachen Zufallsstichprobe die Anzahl möglicher Stichproben?

Die Anzahl der möglichen Stichproben ergibt sich aus dem Verhältnis der Elemente der Population (N) und der gewünschten Stichprobengröße (n).

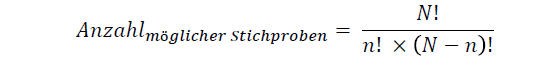
Was ist der Unterschied zwischen Stichprobenkennwerten und Populationsparametern?

• Stichprobenkennwerte = das, was wir aus den Daten der Stichprobe berechnen.

• Populationsparameter = die wahren Werte in der Gesamtpopulation, die wir eigentlich wissen wollen.

• Wir benutzen die Stichprobenkennwerte als Schätzer für die unbekannten Populationsparameter.

Was ist ein Punktschätzer und nach welchen Kriterien wird seine Güte beurteilt?

• Punktschätzer = eine Regel/Formel, die aus einer Stichprobe einen einzelnen Wert (Schätzung) für einen unbekannten Populationsparameter liefert.

Gütekriterien nach Fisher (1925):

1. Erwartungstreue – im Mittel richtig (unverzerrt).

2. Konsistenz – mit wachsender Stichprobe nähert sich der Schätzer dem wahren Wert.

3. Effizienz – unter allen unverzerrten Schätzern der mit der geringsten Streuung.

4. Suffizienz – enthält alle relevanten Informationen über den Parameter.

Merksatz:

Richtig – stabil – präzise – vollständig.

Definiere das Gütekriterium “Erwartungstreue”

Ein Stichprobenkennwert k schätzt den Parameter K einer Population erwartungstreu, wenn der Mittelwert der k-Werte für zufällig aus der Population gezogene Stichproben mit dem Populationsparameter K identisch ist.

Nenne Beispiele für erwartungstreue Schätzer

• Mittelwert

• relative Häufigkeit

• Stichprobenvarianz ist KEIN erwartungstreuer Schätzer

Definiere das Gütekriterium “Konsistenz”

Ein Stichprobenkennwert k schätzt den Parameter K einer Population konsistent, wenn k mit wachsendem Umfang der Stichprobe (n→∞) gegen K konvergiert.

Nenne Beispiele für konsistente Schätzer

• Mittelwert

• relative Häufigkeit

• Stichprobenvarianz

Definiere das Gütekriterium “Effizienz”

Ein Stichprobenkennwert schätzt einen Populationsparameter effizient, wenn die Varianz der Verteilung dieses Kennwertes kleiner ist als die Varianzen der Verteilungen anderer, zur Schätzung dieses Parameters geeigneter Kennwerte. Die Effizienz charakterisiert damit die Genauigkeit einer Parameterschätzung

Wie lassen sich Erwartungstreue und Effizienz von Punktschätzern mit einer Zielscheibe veranschaulichen?

Zielscheibe = wahrer Wert (Populationsparameter)

Pfeile = Schätzungen aus verschiedenen Stichproben

Möglichkeiten:

• Erwartungstreu, aber ineffizient

  →Pfeile sind weit verstreut, aber der Durchschnitt liegt beim Zentrum (=im Mittel richtig, aber ungenau)

• Präzise, aber verzerrt (nicht erwartungstreu)

  →immer daneben, nur sehr konsequent

• Erwartungstreu + effizient

  →Pfeile liegen eng beieinander und genau am Zentrum (=im Mittel richtig und präzise, optimaler Schätzer)

Definiere das Gütekriterium “Suffizienz”

Ein Schätzwert ist suffizient (erschöpfend), wenn er alle in den Daten einer Stichprobe enthaltenen Informationen berücksichtigt, sodass man durch Berechnung eines weiteren statistischen Kennwertes keine zusätzlichen Informationen über den zu schätzenden Parameter erhält

Nenne Beispiele für suffiziente Schätzer

• relative Häufigkeit

• Stichprobenmittelwert und Varianz zusammengenommen (aber nicht allein), bei normalverteilten Zufallsvariablen

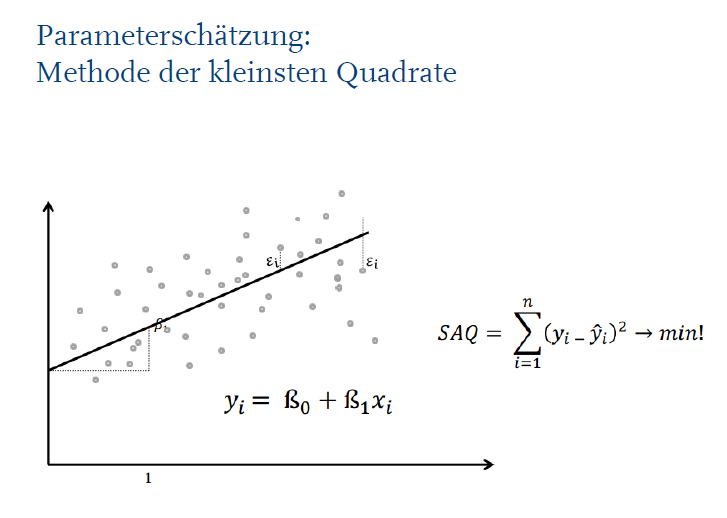
Was bedeutet die Methode der kleinsten Quadrate in der linearen Regression?

• Ziel: Finde die Regressionsgerade, die am besten durch die Datenpunkte passt.

• Jeder Datenpunkt liegt oft nicht genau auf der Geraden → die Abweichungen heißen Residuen

• Methode: Wir suchen die Gerade so, dass die Summe der quadrierten Residuen (Fehler) minimal ist:

• „Quadrate“ deshalb, weil die Abweichungen zum Quadrat genommen werden → verhindert, dass sich positive und negative Fehler aufheben.

• Anschaulich:

  • Stell dir vor, du legst eine Linie durch eine Punktewolke.

  • Die Linie gilt als „beste Gerade“, wenn die vertikalen Abstände zu allen Punkten im Quadrat möglichst klein sind.

Was bedeutet die Maximum-Likelihood-Methode bei der Parameterschätzung?

• Idee: Wir suchen den Parameterwert, bei dem die beobachteten Daten am wahrscheinlichsten sind.

• Dazu definieren wir eine Likelihoodfunktion:

  L(θ)=P(Daten∣θ)

  → Wahrscheinlichkeit der Daten gegeben einen bestimmten Parameter θ

• Wir vergleichen verschiedene Parameterwerte und wählen denjenigen, bei dem L(θ) maximal ist.

• „Die Maximum-Likelihood-Methode sucht denjenigen Parameterwert, bei dem die beobachteten Daten am wahrscheinlichsten sind. Man baut dafür eine Likelihoodfunktion auf und schaut, wo diese ihr Maximum hat. Beispiel: Wenn 5 von 12 Leuten bestehen, dann liegt die höchste Likelihood bei einem Erfolgsanteil von ca. 0,42 – das wäre unser Schätzer.“

Vergleiche die Methode der kleinsten Quadrate und die Maximum Likelihood. Was sind die Unterschiede?

Methode der kleinsten Quadrate (OLS):

• Ziel: Gerade finden, die Abstände (Residuen) zwischen vorhergesagten und beobachteten Werten minimiert.

• Typisch: Lineare Regression.

• Intuition: „Beste Gerade = kleinste Fehlerquadrate.“

Maximum-Likelihood (ML):

• Ziel: Parameter finden, die die beobachteten Daten am wahrscheinlichsten machen.

• Typisch: Schätzung in vielen Modellen (Regression, Logit, SEM, etc.).

• Intuition: „Beste Parameter = machen meine Daten am plausibelsten.“

Zusammenhang:

• Bei normalverteilten Fehlern führen OLS und ML zur gleichen Schätzung.

• Unterschied: OLS basiert direkt auf Fehlerquadraten, ML auf Wahrscheinlichkeiten.

---

Mini-Merksatz:

• OLS = minimaler Fehler

• ML = maximale Wahrscheinlichkeit

Was ist ein Intervallschätzer?

Verfahren, mit dessen Hilfe ein Parameter durch ein Intervall vom Typ a<Populationsmittelwert<b geschätzt wird (Verfahren ermittelt Grenzen, innerhalb derer sich der wahre Populationsparameter mit hoher Plausibilität befindet (Konfidenzintervall)

Was besagt das zentrale Grenzwerttheorem?

Das Zentrale Grenzwerttheorem sagt:
👉 Wenn du die Stichproben groß genug machst (meist ab n ≈ 30), dann sind die Stichprobenmittelwerte annähernd normalverteilt – egal, wie die Ausgangsverteilung aussieht!

Lernkontrollfragen 1 :Was ist eine einfache Zufallsstichprobe?

Wenn alle Elemente aus der Population (N) die gleiche Ziehungswahrscheinlichkeit haben.

Lernkontrollfrage 2: Wann ist eine einfache Zufallsstichprobe repräsentativ?

• Folgendes muss erfüllt sein:
  
  merkmalsspezifisch repräsentativ: die Stichprobe entspricht in für den für die Untersuchung relevanten Merkmalen der Population

  global repräsentativ: die Stichprobe entspricht in nahezu allen Merkmalen der Population.

Lernkontrollfrage 3: Gib für die Kritien unbiased, precise und accurate an, wie sich diese mit den vier Kriterien Erwartungstreue, Konsistenz, Effizienz und Suffizienz ausdrücken lassen.

Vergleich mit Zielscheiben:

• unbiased: Erwartungstreu, aber ineffizient

  →Pfeile sind weit verstreut, aber der Durchschnitt liegt beim Zentrum (=im Mittel richtig, aber ungenau)

• precise: Präzise, aber verzerrt (nicht erwartungstreu)

  →immer daneben, nur sehr konsequent

• accurate: Erwartungstreu + effizient

  →Pfeile liegen eng beieinander und genau am Zentrum (=im Mittel richtig und präzise, optimaler Schätzer)

Lernkontrollfrage 4: Was ist ein Punktschätzer, was ein Intervallschätzer?

• Punktschätzer

  • Liefert einen einzelnen Wert als Schätzung für einen Populationsparameter.

• Intervallschätzer

  • Liefert einen Bereich, in dem der wahre Parameter mit einer bestimmten Wahrscheinlichkeit liegt.

  • Beispiel: 95%-Konfidenzintervall [170 cm ; 174 cm].

Merksatz:

• Punktschätzer = ein Wert

• Intervallschätzer = Wertbereich + Sicherheit

Lernkontrollfrage 5: wie “funktioniert” eine Maximum Likelihood Schätzung?

Frage: Wie funktioniert eine Maximum-Likelihood-Schätzung?

Antwort (prüfungsreif, in eigenen Worten):

• Die Maximum-Likelihood-Methode sucht denjenigen Parameterwert, bei dem die Wahrscheinlichkeit für die beobachteten Daten am größten ist.

• Dazu wird eine Likelihoodfunktion aufgestellt:

  L(θ)=P(Daten∣θ) Dann vergleicht man verschiedene mögliche Parameterwerte und wählt denjenigen, bei dem L(θ) maximal ist.

• Beispiel: Wenn 5 von 12 Personen eine Prüfung bestehen, dann liegt die Likelihood am höchsten bei einem Erfolgsanteil p≈0,42. → das ist der Maximum-Likelihood-Schätzer p^\hat{p}p^​.

---

🎯 Merksatz

👉 „Maximum Likelihood = Parameter wählen, die meine Daten am plausibelsten machen.“

---

💡 Bildliche Vorstellung

• Stell dir vor, du probierst verschiedene „Hypothesen“ über den wahren Parameter aus.

• Für jede Hypothese berechnest du: „Wie wahrscheinlich sind meine Daten, wenn das stimmt?“

• Dann nimmst du die Hypothese, bei der deine Daten am wahrscheinlichsten wären → das ist der MLE.

Was bedeutet Modellvergleich in der multiplen Regression?

• Idee: Prüfen, ob ein komplexeres Modell (mit mehr Prädiktoren) die AV besser erklärt als ein einfacheres Modell.

• Nullmodell: Nur der Mittelwert wird vorhergesagt
  Note=β0+ε\text{Note} = \beta_0 + \varepsilonNote=β0​+ε.

• Einfaches Modell mit 1 UV:
  Note=β0+β1⋅Intelligenz+ε\text{Note} = \beta_0 + \beta_1 \cdot \text{Intelligenz} + \varepsilonNote=β0​+β1​⋅Intelligenz+ε.

• Vergleich: Wie viel zusätzliche Varianz erklärt das Modell mit Prädiktor(en) im Vergleich zum Nullmodell?

Merksatz:
👉 Nullmodell = nur Mittelwert
👉 Modellvergleich = bringt ein zusätzlicher Prädiktor bessere Vorhersage?