Analyzing Categorical Variable II

What are observed values in a Goodness of Fit test?

Observed values (O) are the actual counts or frequencies collected from your data.

Give an example of observed values.

If you counted ear usage in 25 people and got 19 right and 6 left, those are your observed values.

What are expected values in a Goodness of Fit test?

Expected values (E) are the counts you would expect if the null hypothesis were true.

How do you calculate expected values in a Goodness of Fit test?

You calculate expected values using the probability distribution from the null hypothesis.

If the null hypothesis states a 50/50 distribution, what are the expected values for 25 trials?

Right: 25×0.5=12.5 and Left: 25×0.5=12.5.

What is the Chi-Square test, and when is it used?

It Compares observed values to expected values using squared differences. Used with simpler data, it is the most common goodness of fit test.

What is the G-test and when is it used?

Compares observed values to expected values using logarithms (likelihood ratios).

Often more accurate for large sample sizes or when dealing with very small expected counts.

What is the purpose of a Goodness-of-Fit Test?

To see if one categorical variable matches an expected distribution.

When should you use a Test of Association/Independence?

When you want to see if two or more categorical variables are related.

Example of when to use the Goodness of Fit Test

You predict 50% of seeds will be round and 50% wrinkled, but you observe 60% round and 40% wrinkled.

Example of Test of Independence/Association

You test whether fertility (fertile/sterile) depends on location (France/India) in flies.

How do you calculate df for a chi-squared goodness-of-fit test?

df = (# categories - 1)

When do you use df = (# of categories - 1)?

For one categorical variable (goodness-of-fit test).

: When do you use df = (rows – 1)(columns – 1)?

For two categorical variables (test of independence/association).

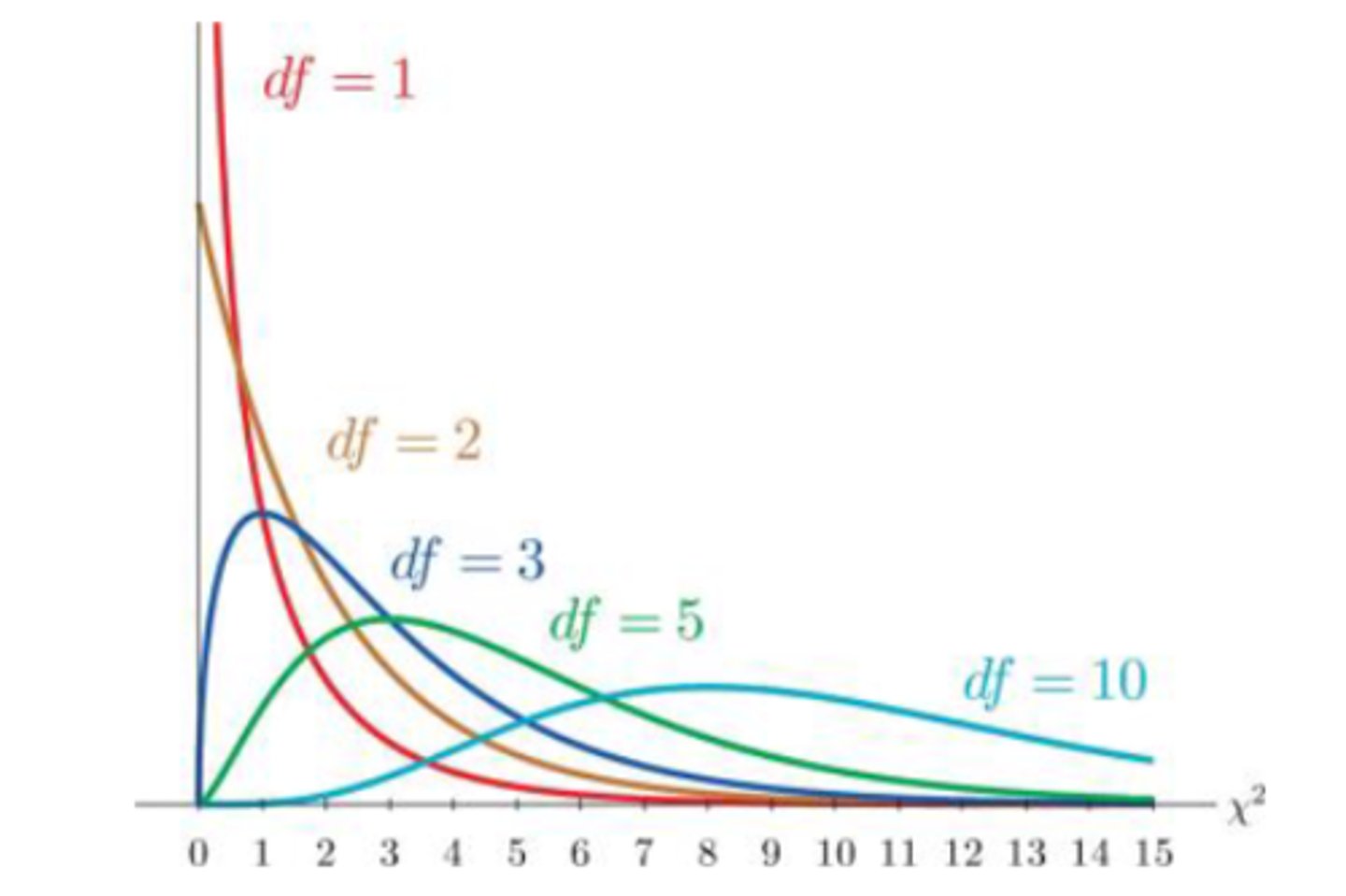
How does the chi-squared (χ²) distribution change as degrees of freedom (df) change?

At low df: looks like an exponential distribution (df = 1)

Then: strongly right-skewed (df = 2-5)

At higher df: becomes more symmetrical but platykurtic (df=10)

What is the first step in interpreting Chi-Square and G-test results?

State hypotheses

Null hypothesis (H₀): Observed data matches expected counts (goodness-of-fit) or variables are independent (test of independence).

Alternative hypothesis (Hₐ): Observed data does not match expected counts or variables are dependent.

How do you interpret Chi-Square test results?

Compare X² to the critical value or p-value to 0.05.

What does it mean if X² is greater than or equal to the critical value or p is less than or equal to 0.05?

Reject H₀ (data differs from expected).

What does it mean if X² is less than the critical value or p is greater than 0.05?

Fail to reject H₀ (data matches expected).

How do you interpret a G-test of association/independence?

If G ≥ critical value or p ≤ 0.05 → reject H₀ (variables are associated/dependent)

If G < critical value or p > 0.05 → fail to reject H₀ (variables are independent)

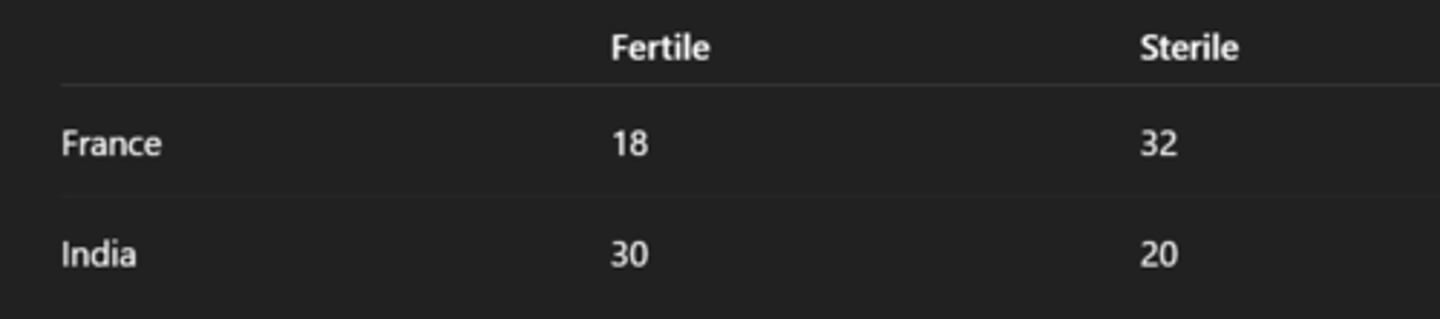
Set up a 2×2 contingency table using the following observed data on fertility of males from France and India:

France (Fertile) = 18

France (Sterile) = 32

India (Fertile) = 30

India (Sterile) = 20

Contingency table should look like this

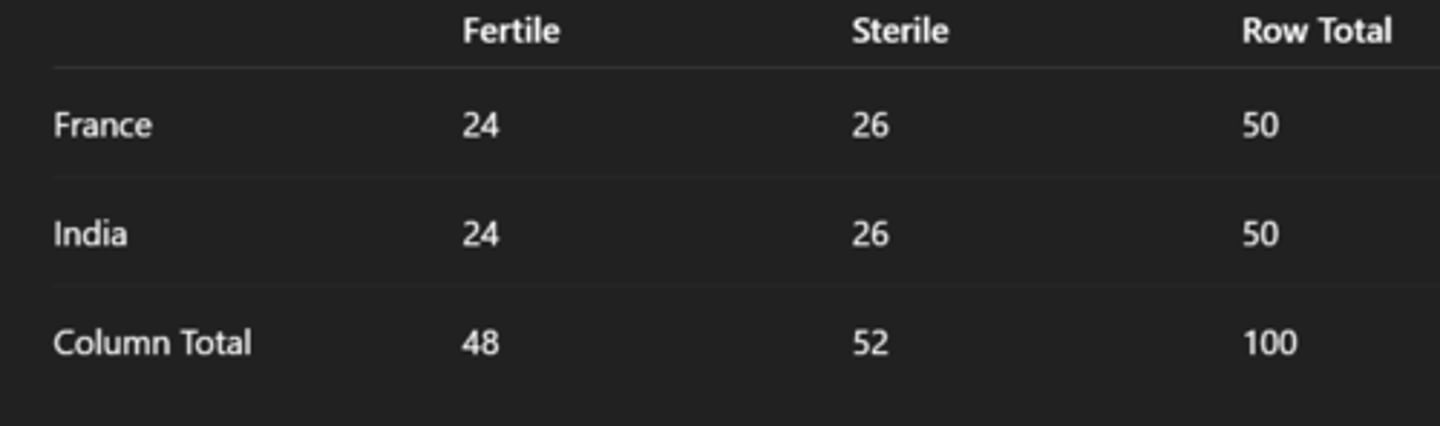
Now, calculate the row totals, column totals, and grand total.

Row, column, and grand totals should equal this. Grand total should be all the data added together.

Using the observed data below, calculate the expected values for each cell in a 2×2 contingency table.

(Row i total×Column j total)​

-------------------------------

Grand total

Example: From France and Fertile

50 (corresponding row total) x 48 (Corresponding column total) / 100 (grand total)

= 24 (expected value)

What is Yates' correction and why use it?

Used in 2×2 tables when counts are small.

Makes the test more reliable (less likely to say there’s an effect when there isn’t, Type 1 Error)

How do we adjust counts with Yate's correction?

Adjust the counts depending on the sign of ad−bc

If ad−bc > 0

Add 0.5 to b and c

Subtract 0.5 from a and d

If ad−bc < 0

Subtract 0.5 from b and c

Add 0.5 to a and d

When do you use Fisher's exact test?

2×2 tables with small counts (any observed or expected cell ≤ 5).

Better than Yates’ correction for tiny samples.

How does Fisher's exact test work?

Calculates an exact p-value using factorials of row totals, column totals, cell counts, and grand total.

No expected counts are needed.

How to interpret Fisher's exact test?

How to interpret:

p ≤ 0.05 → reject null → variables are associated.

p > 0.05 → fail to reject null → no evidence of association.

How do the odds ratio and relative risk differ, and how do you interpret them?

Odds Ratio: Measures odds of success in one group vs another: OR = ad/bc

Relative Risk: Measures probability (risk) of failure/success in treatment vs control:

How to interpret the odds ratio?

OR > 1 → success more likely in first group

OR < 1 → success less likely in first group

How to interpret Relative Risk?

RR = 1 → no difference

RR < 1 → risk lower in first group

RR > 1 → risk higher in first group