Waves - Refraction and Polarization - Model Answers

1. Explain what is meant by refraction.

Refraction is the change in direction of a wavefront as it changes speed due to a change in the density of the medium that it is travelling in.

2. Define the refractive index.

Refractive index, n = c/v. This is the ratio of the speed of light in a vacuum to the speed of light in the medium.

3. Explain how to experimentally determine the refractive index of glass.

• Measure the angle of refraction, θr, for a ray for 6 different value of the angle of incidence, θi.

• Plot a graph of sin θr against sin θi.

• sin θr = (1/n2)(sin θi). Here n1 = 2 as first material is air.

• y = m x

• So the gradient is 1/n2, determine the gradient and n2 = 1/gradient.

4. Define critical angle

The angle of incidence in the denser medium at which the angle of refraction is 90 degrees in the less dense medium : sin c = 1/n.

5. Describe the condition for total internal reflectiion to occur.

• The light has to be travelling in the denser medium.

• Total internal reflection will occur when the angle of incidence is larger than the critical angle. θi > θc.

6. a) Principal focus (focal point)

The point on the princial axis where rays parallel to the principal axis (from a very distant object) will converge.

6. b) Focal length, f

The distance between the centre of the lens and the principal focus (is negative for diverding lengthes and positive for converging lenses).

6. c) Image distance, v

The distance between the image and the centre of the lens (is negative for virtual images and positive for real images).

6. d) Object distance, u

The distance between teh object and the centre of the lens.

6. e) Magnification

Magnification = v/u or the image height/object height (hi/ho). No unit.

6. f) Converging lens

A lens that causes rays to converge on the principal axis - has a positive focal length.

6. g) Diverging lens

A lens that causes rays to diverge after refraction - has a negative focal length.

Power of a diverging lens is negative.

6. h) Power

Power = 1/f = 1/focal length. Units = D (dioptres).

When multiple lenses are lined up on the principal axis, their powers add up (subtract for diverging lenses).

6. i) Virtual image

An image fromed from the apparent divergence of rays from an object.

Cannot be projected on a screen.

6. j) Real image

An image formed when real rays of light converge to form the image. Can be projected on a screen.

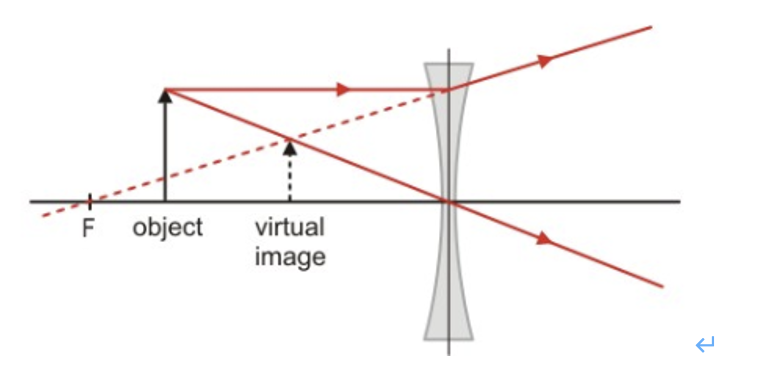
7. Construct a ray diagram for diverging lens with the object placed before the focal length.

SEE DIAGRAM:

• Virtual

• Upright

• Diminished

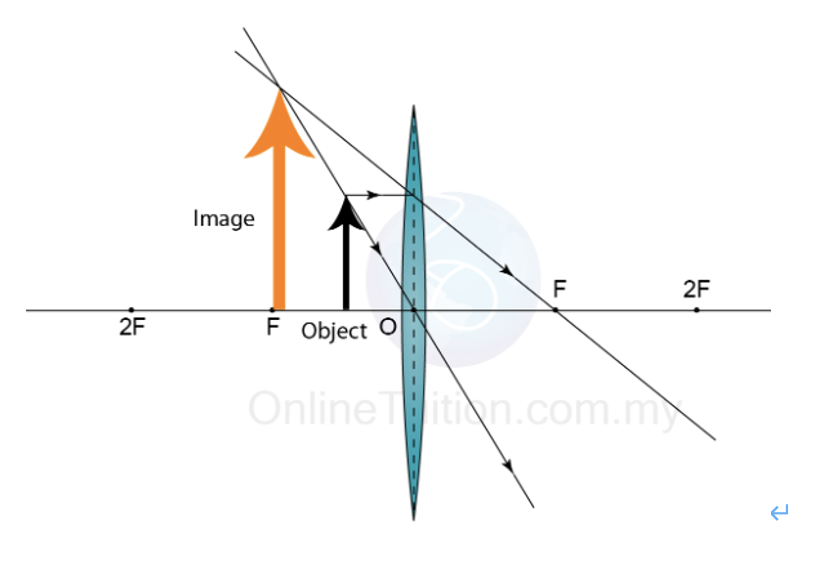
8. Construct a ray diagram for a converging lens with the object at half the focal length.

SEE DIAGRAM

• Virtual

• Upright

• Magnified

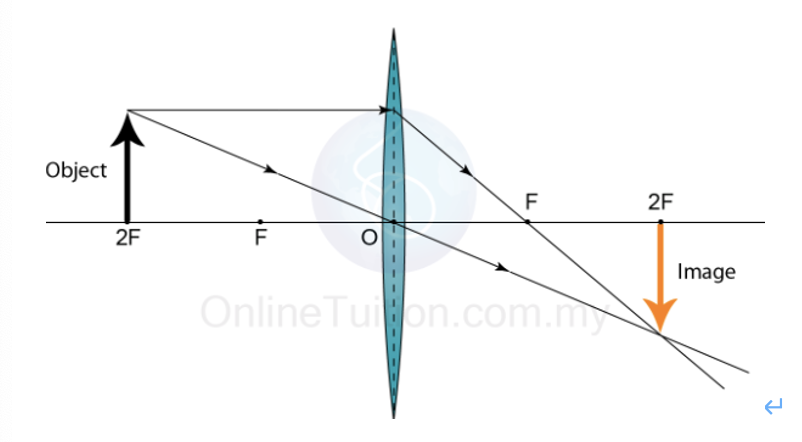
9. Construct a ray diagram for a converging lens with the object at twice the focal length.

SEE DIAGRAM

• Real

• Inverted

• Same size

10. Explain how to estimate the focal length, f, of a converging lens.

• Pass parallel rays of light from a distant object through the lens and move a screen behind the lens until the image is focussed.

• The distance between the lens and the focused image is an estimate of the focal length.

11. Explain how to determine the focal length of a lens accurately.

• Place an object (e.g. lamp behind cut out shape) on a ruler, 10 cm in front of a lens in a lens holder (independent) and infront of a screen.

• Move the screen until an image in focused on the screen.

• Record the positions of the screen, lens and object.

• Calculate image distance, v = lens dstance - screen distance. Object distance, u = lens distance - object distance.

• Repeat steps 1 - 4 for five different objet distances, u.

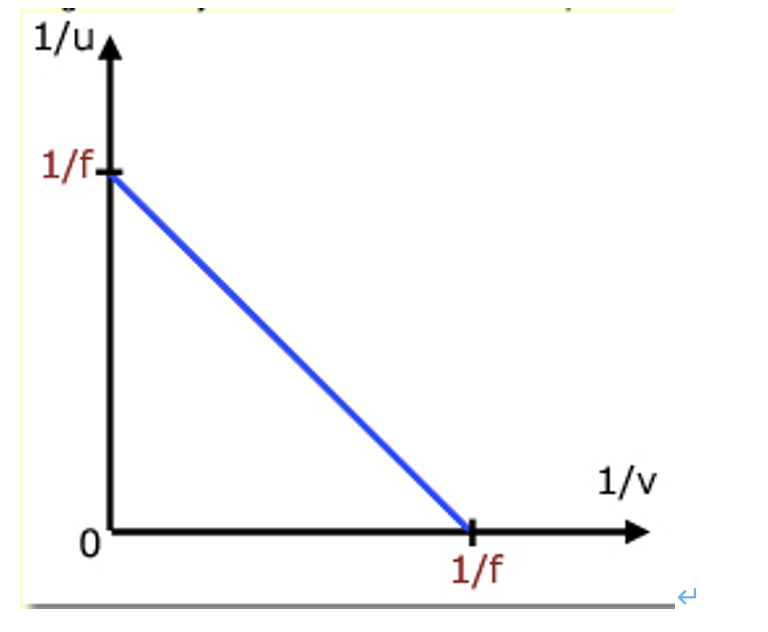
• Plot a graph of 1/u against 1/v.

• 1/u = -1/v + 1/f

• y = m x + c

• The gradient should be -1

• Determine the x and y intercepts.

• f = 1/x intercept and 1/y intercept

• Take an average of the intercepts of the f values.

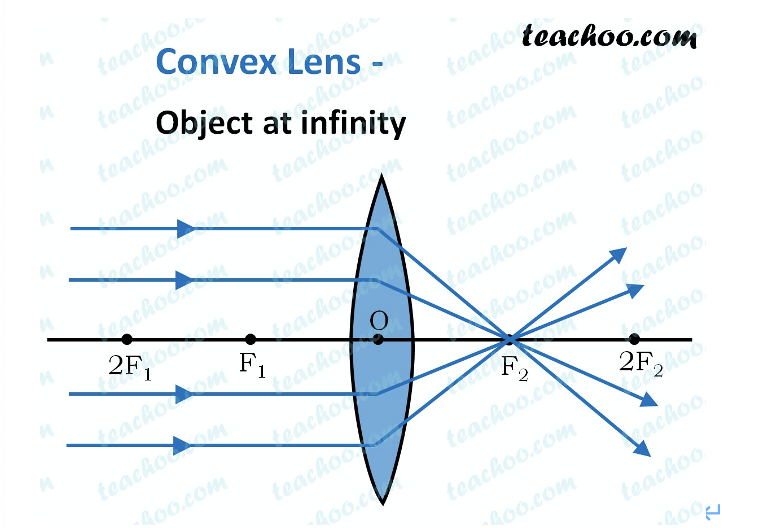
12. When would the rays from an object converge at the focal point.

• Only when the inciden rays are parallel to the pricipal axis.

• This happens when the object is at an infinite distance from the lens.

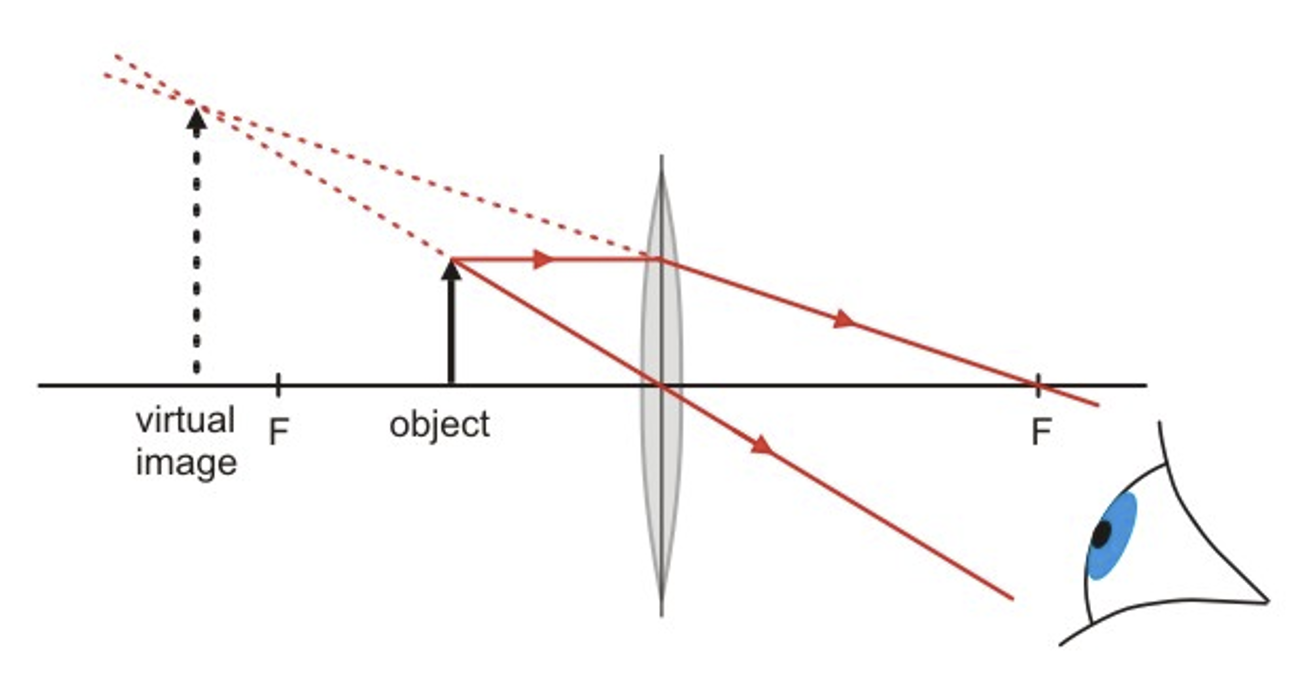
13. What happens if an object is placed closer to a converging lens than the focal point. f < u

• When the object distance is less than the focal length ( f < u ), a virtual image is formed behind the lens.

• This is because the rays of light diverge after the lens.

• Causing virtual rays to converge on the same side of the lens as the object.

• These cannot be projected onto a screen.

• The lens is behaving as a magnifying glass.

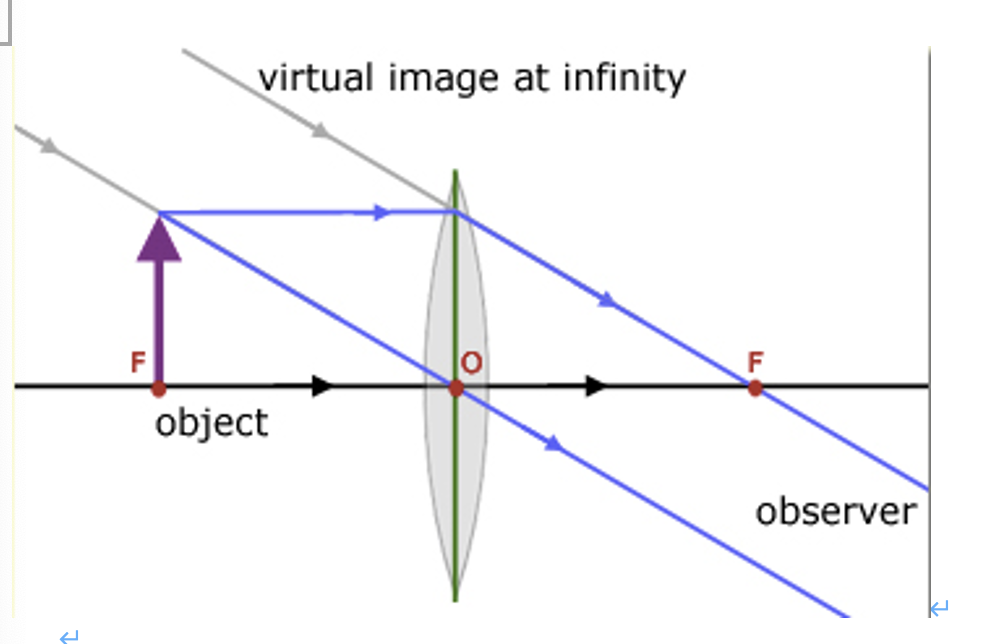
14. Draw a ray diagram for a magnifying glass.

Convex lens, with object closer than the focal point.

15. Describe the situations when a virtual image may form from a real object placed infront of the lens.

• All images of real objects made by diverging lenses are virtual.

• Images formed by objects placed closer than the focal point - converging lens.

16. Explain wht a converging lens will not produce an image when the object is placed at the focal point.

• If image distance = focal length (u = f), then 1/f = 1/u + 1/v becomes

• 1/u = 1/u + 1/v

• so 1/v = 0

• So image distance, v would be infinate - there is no image formed.

• This is because one way passes through the focal point on the right hand side of the lens.

• And another ray passes trough the centre of the lens.

• These rays (and all others) are parallel, and therefore do not converge.

• Nor do they diverge, so a virtual image cannot be made either.

17. Define unpolarised light.

Unplarised light has oscillations (of the fields) in all directions.

18. Define polarised light.

• Polarised light is EM radiation.

• Where the osciallations of the electric field is in a single plane.

• And that plane includes the direction of energy transfer / propagation.

OR

• Polarised light is EM radiation.

• Where the oscillations of the electric field is in one direction.

• The direction of oscillation is perpendicular to the direction of energy transfer/ propagation.

19. Explain what a polarising filter does to unpolarised light.

• A polarizing filter absorbs all components of the (light’s) oscillation that are perpendicular to the plane of polarisation of the filter.

• The filter transmits all the components of the (light’s) oscillations that are parallel to the plane of polarisation of the filter.

• This reduces the intensity of unpolarised light to half, and produces polarised light, that oscillates in one plane. With the plane being the plane of polarisation of the filter (and includes the direction of propagation/ energy transfer).

20. Explain what a polarizing filter does to polarised light.

• A polarizing filter absorbs all components of the (light’s) oscillation that are perpendicular to the plane of polarisation of the filter.

• The filter transmits all components of the (light’s) oscillation that are parallel to the plane of polarizstion of the filter.

• This means that when the plane of polarisation of the filter is parallel to the plane of polarisation of the polarised light, all of the polarised light is transmitted, and the intensity remains the same before and after the filter.

• This means that when the plane of polarisation of the filter is perpendicular to the plane of polarisation of the polarised light, all of the polarised light is absorbed and the intensity becomes zero.

(Remember to talk about when the angle is 90,270 degrees and when the angle 0, 180 degrees - talk about two angles, and also refer to the cycle every 90 degrees).

21. Explain why longitudinal waves cannot be polarised.

• Longitudinal waves oscillate parallel to the direction of propagation/ energy transfer.

• So this oscillatiion direction cannot be removed without also removing the propagation of the wave.

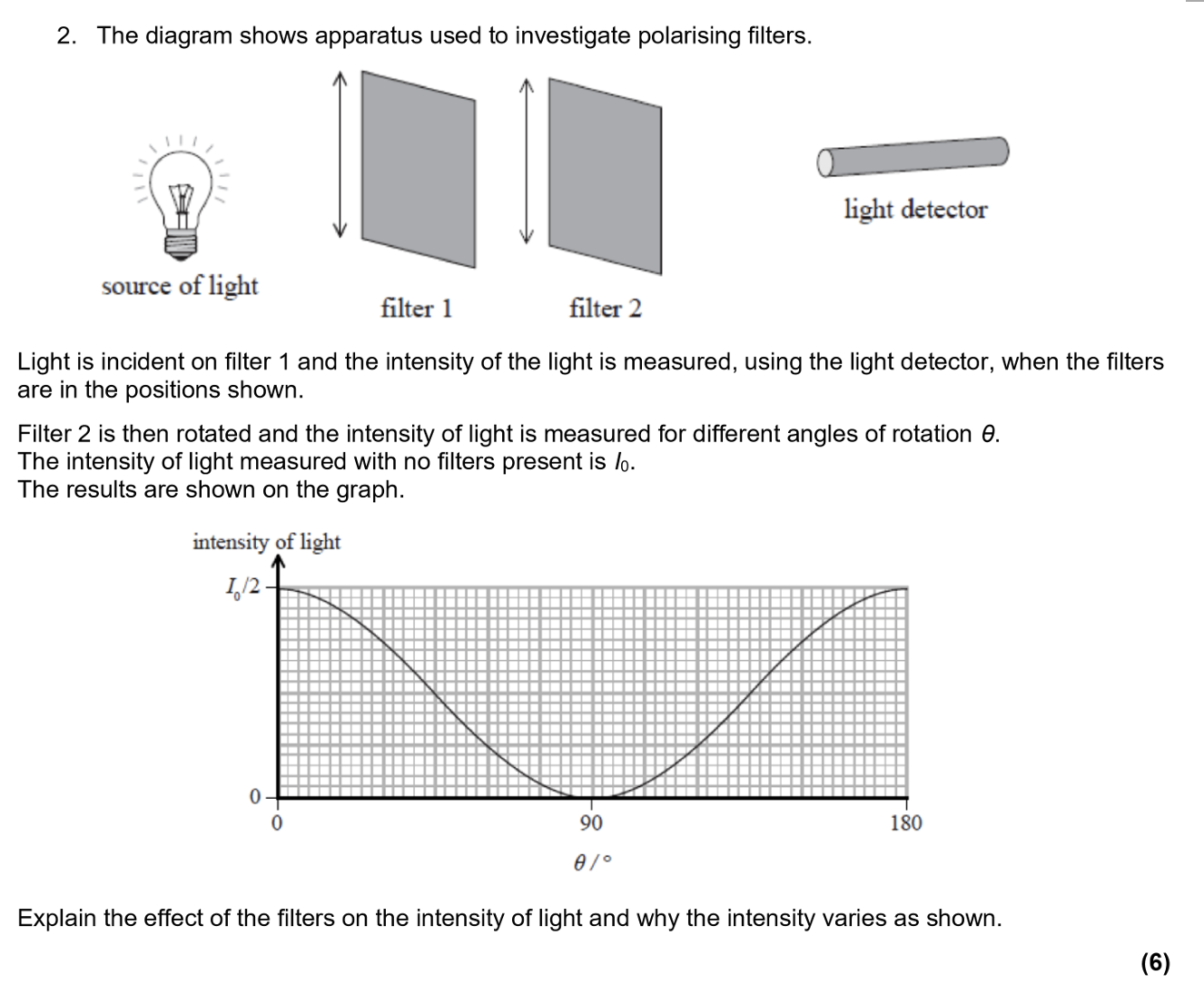
22. SEE QUESTION

• Light from the souce is unpolarised - the oscillations occur in all planes/directions.

• As the unpolarised light passes through the first filter, the intensity reduces to half.

• This is because filter 1 absorbs all oscillation (of light) that are perpendicular to the filter’s plane of polarisation.

• When the second filter is aligned at 0 or 180 degrees to the first filter, all the polarised light (at intensity I0/2) is transmitted.

• As the second filter is rotated, the polarised light’s plane of polarisation is no longer completely parallel to the filter’s plane of polarisation. Perpendicular components of the light’s oscillation are absorbed and parallel components are transmitted. So intensity of light decreases.

• When the second filter is aligned at 90 or 270 degrees to the first filter, all the polarised light (at intensity I0/2) is absorbed because the second filter’s plane of polarisation is entirely perpendicualr to the light’s plane of polarisation, and the intensity is zero.

23. Explain how to use one filter to demonstrate whether a source of EM radiation is polarised of not.

• Hold the filter up to the light source and rotate it.

• If the light is polarised, the intensity will cycle from maximum to zero, every 90 degrees.

• If the light is unpolarised, the intensity will reduce to half its original value but remain constant as the filter is rotated.

24. SEE QUESTION

• As the filters are places with their planes of polarisation at 90 degress to one another, all light that has not had its plane of polarisation rotated would be absorbed.

• So where light is transmitted, must indicate that the plane of polarisation has been rotated due to stress.

• So the brighter areas represent more stress where roatation has happened, and the darker areas represent less stress where rotation has not happened.

25. A student looks at the sunlight reflected off a puddle of water. She puts a polarising (Polaroid) filter in front of her eye. As she rotates teh filter, the puddle appears darker then lighter. Explan this observation.

• This indicates that reflected sunlight is polarised.

• Meaning its oscillations are only in one plane.

• When the polarising filter’s plane of polarisation is parallel to the plane of polarisation of the sunlight, the EM radiation is transmitted, and the intensity is high.

• After rotating 90 degrees, the polarising filter’s plane of polarisation is perpendicular to the plane of polarisation of the sunlight. The EM radiation is absorbed and the intensity is zero.