Buffers and Titrations

from powerpoint

what is a buffer?

solutions that resist changes in pH when an acid or base is added - •they act by neutralizing the added acid or base

what does a buffer solution contain?

contains a combination of acid-base conjugate pairs, (means it may contain a weak acid and its conjugate base or a weak base and its conjugate acid )

Example problem: How do you prepare a buffer using HF and NaF? READS: How many moles of NaF must be added to 0.5 L of 0.2 M HF to make a buffer with pH = 3.50?

Ka=6.8×10^-4

How many moles of NaF must be added to 0.5 L of 0.2 M HF to make a buffer with pH = 3.50?

Ka=6.8×10^-4

pKa=-log(Ka)

pKa=3.17

0.2M HF * 0.5L = 0.1M

Solution:

1. Henderson-Hasselbalch Equation:

2. pH=pKa+log(f-/HF)

   3.50=3.17+log⁡([F−]/0.1)

3. Solve for [F−]

   3.50−3.17=log⁡([F−]/0.1)

4. 0.33=log⁡([F−]/0.1)

5. 10^0.33≈2.14

6. [[F−]/0.1]=2.14

7. [F-] = 0.214

8. 0.214 moles = NaF

Describe how to use a salt to make a buffers ( weak acid conjugate pair)

Example: How does adding sodium acetate (CH₃COONa) help create a buffer with acetic acid (CH₃COOH)?

1. Salt Dissociation:

   CH3COONa→CH3COO−+Na+CH₃COONa \to CH₃COO^- + Na^+CH3​COONa→CH3​COO−+Na+

   • Increases CH₃COO⁻ (conjugate base) concentration.

2. Shifts Equilibrium Left:

   CH3COOH+H2O⇌CH3COO−+H3O+

   • More CH₃COO⁻ suppresses acid dissociation (Le Chatelier’s Principle).

   • Lowers H₃O⁺ concentration, stabilizing pH.

3. Buffer Effect:

   • Resists pH changes when acid (H₃O⁺) or base (OH⁻) is added.

Describe how to use a salt to make a buffers ( weak Base conjugate pair)

How does adding ammonium chloride (NH₄Cl) help create a buffer with ammonia (NH₃)?

• Salt Dissociation:

  NH4Cl→NH4++Cl−NH₄Cl \to NH₄^+ + Cl^-NH4​Cl→NH4+​+Cl−

  • Increases NH₄⁺ (conjugate acid) concentration.

• Shifts Equilibrium Left:

  NH3+H2O⇌OH−+NH4+NH₃ + H₂O \rightleftharpoons OH^- + NH₄^+NH3​+H2​O⇌OH−+NH4+​

  • More NH₄⁺ suppresses base dissociation (Le Chatelier’s Principle).

  • Lowers OH⁻ concentration, stabilizing pH.

• Buffer Effect:

  • Resists pH changes when acid (H₃O⁺) or base (OH⁻) is added.

How to make a buffer through strong/base neutralization or adjust the ratio of the conjugate of the acid / base pair

How can you create a buffer using HF and a strong base?

• Add a Strong Base (e.g., NaOH) to HF Solution:

  • NaOH neutralizes some HF, forming F⁻ (its conjugate base).

  HF+OH−→F−+H2O

• Adjust the Ratio of HF to F⁻:

  • Use the Henderson-Hasselbalch equation to set the desired pH:

    pH=pKa+log⁡([F−][HF])

  • Adding more NaOH increases F⁻, shifting pH up.

  • Adding more HF increases HF, shifting pH down.

• Result:

  • The HF/F⁻ system now acts as a buffer, resisting pH changes.

Which combination when mixed makes a buffer solution(assume large amounts of reactant are left over  

A.  HCl and KCl

B.  H₂CO₃  and NaHCO₃

C.  H₃PO₄ and NaCl

D.CH₃COOH and CH₃COOK

E.NH₃ and NH₄Cl

✅ B. H₂CO₃ and NaHCO₃ (carbonic acid & bicarbonate, weak acid/conjugate base)
✅ D. CH₃COOH and CH₃COOK (acetic acid & acetate, weak acid/conjugate base)
✅ E. NH₃ and NH₄Cl (ammonia & ammonium, weak base/conjugate acid)

Why Not the Others?

❌ A. HCl and KCl – HCl is a strong acid, no buffer.
❌ C. H₃PO₄ and NaCl – NaCl does not provide a conjugate base.

Which combination makes a buffer solution with the use of salts? ( Assume large amounts of everything ) 

A.  HI and NaOH

B.  H₂CO₃  and NaOH

C.NH₃ and NaOH

D.NH₃ and HNO3

HF + LiOH

The combinations that form buffer solutions using salts are:

✅ B. H₂CO₃ and NaOH → Forms HCO₃⁻ (bicarbonate), creating a H₂CO₃/HCO₃⁻ buffer
✅ E. HF and LiOH → Forms F⁻, creating an HF/F⁻ buffer

Why Not the Others?

❌ A. HI and NaOH → HI is a strong acid, no buffer.
❌ C. NH₃ and NaOH → Both are bases; no weak acid to form a buffer.
❌ D. NH₃ and HNO₃ → Strong acid fully reacts with NH₃, leaving no weak base/conjugate

The addition of hydrofluoric acid and _____ to water produces a buffer solution

A. NaBr

HCL

NaNO3

NaOH

NaCl

NaOH

Explanation:

• HF is a weak acid, and NaOH is a strong base.

• When NaOH is added to HF, it neutralizes part of the HF, forming F⁻ (fluoride ion), which is the conjugate base of HF.

• This creates a HF/F⁻ buffer system that can resist pH changes.

Why Not the Others?

❌ NaBr, HCl, NaNO₃, NaCl – None of these form a buffer solution with HF because they do not provide a conjugate base or acid.

which one of the following pairs cannot be mixed together to form a buffer solution

A. NaCL, HCL

b. HONH2, HONH3Cl

c. KOH, HNO2

d. H2SO3, KHSO3

E. RbOH, HF

The pair that cannot form a buffer solution is:

❌ A. NaCl, HCl

Explanation:

• NaCl is a neutral salt, and HCl is a strong acid. A buffer requires a weak acid and its conjugate base (or a weak base and its conjugate acid). HCl dissociates completely in water and does not provide a conjugate base to form a buffer.

Why the Others Work:

• B. HONH₂ and HONH₃Cl: HONH₂ (hydroxylamine) is a weak base, and HONH₃Cl is its conjugate acid, forming a buffer.

• C. KOH and HNO₂: KOH (strong base) neutralizes some of the HNO₂ (weak acid), creating the conjugate base NO₂⁻, forming a buffer.

• D. H₂SO₃ and KHSO₃: H₂SO₃ (weak acid) and HSO₃⁻ (its conjugate base) form a buffer system.

• E. RbOH and HF: RbOH (strong base) neutralizes part of HF (weak acid), creating the conjugate base F⁻, forming a buffer.

What is the pH of a buffer that is 0.100 M HC₂H₃O₂ and 0.100 M NaC₂H₃O₂?
K_a for HC₂H₃O₂ = 1.8 x 10^-5

HC₂H₃O₂ + H₂O ⇋ C₂H₃O₂- + H₃O⁺

Step 1: Calculate pKa pKa=−log⁡(1.8×10−5)≈4.74\

Step 2: Apply the Henderson-Hasselbalch equation

Given:

• [A⁻] = 0.100 M (from NaC₂H₃O₂)

• [HA] = 0.100 M (from HC₂H₃O₂)

pH=4.74+log⁡(0.100/.100)

pH=4.74+log(0.100/0.100​)

pH=4.74+log⁡(1)

ph = 4.74 + 0

The pH of the buffer solution is 4.74.

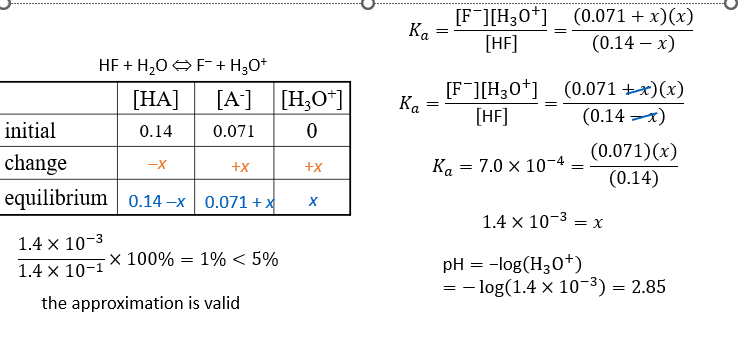
Practice - What is the pH of a buffer that is 0.14 M HF and 0.071 M KF? K_a for HF = 7.0 x 10^-4

Ice table and Ka calculation - see image for example

What is the final pH after adding 0.010 moles of HCl to 500.0 ml of a 0.125 M HC2H3O2 and 0.115 M NaC2H3O2 buffer system.

Step 1: Write the balanced equation for the buffer system

The buffer consists of HC₂H₃O₂ (acetic acid) and its conjugate base C₂H₃O₂⁻ (acetate ion). The reaction between acetic acid and the strong acid HCl is:

HC₂H₃O₂+HCl→C₂H₃O₂−+H₂O

Step 2: Determine the initial moles of acid and base

Given:

• Volume of the buffer solution = 500.0 mL = 0.500 L

• 0.125 M HC₂H₃O₂ (acetic acid) and 0.115 M NaC₂H₃O₂ (acetate ion).

Initial moles:

• HC₂H₃O₂ (acetic acid):

  moles of HC₂H₃O₂=0.125 M×0.500 L=0.0625 moles

• C₂H₃O₂⁻ (acetate ion):

  moles of C₂H₃O₂⁻=0.115 M×0.500 L=0.0575 moles

Step 3: Add the strong acid (HCl)

You are adding 0.010 moles of HCl to the buffer system.

• HCl dissociates completely, so it adds 0.010 moles of H⁺ to the solution.

• The added H⁺ will react with C₂H₃O₂⁻ (the conjugate base) to form more HC₂H₃O₂ (acetic acid).

Step 4: Adjust the moles of acid and base after the neutralization

• C₂H₃O₂⁻ (conjugate base) will decrease by 0.010 moles because it reacts with the H⁺ from HCl.

• HC₂H₃O₂ (acetic acid) will increase by 0.010 moles.

So the final moles are:

• HC₂H₃O₂:

  0.0625 moles+0.010 moles=0.0725 

• C₂H₃O₂⁻:

  0.0575 moles−0.010 moles=0.0475 moles

Step 5: Use the Henderson-Hasselbalch equation

Now, we can apply the Henderson-Hasselbalch equation to find the final pH:

pH=pKa+log⁡([C₂H₃O₂−][HC₂H₃O₂])

First, calculate the new concentrations in the 500.0 mL (0.500 L) solution:

• [HC₂H₃O₂]:

  0.0725 moles0.500 L=0.145 M

• [C₂H₃O₂⁻]:

  0.0475 moles0.500 L=0.095 M

Step 6: Calculate the pH

• pKa for acetic acid (HC₂H₃O₂) is 4.74.

pH=4.74+log⁡(0.0950)(.145)]

pH=4.74+log⁡(0.655)

pH=4.74+(−0.183) pH=4.56

pH=4.56 Answer:

The final pH of the buffer after adding 0.010 moles of HCl is 4.56.

Calculate the pH of a buffer that is 0.225 M HC₂H₃O₂ and 0.162 M KC₂H₃O₂.  The K_a for HC₂H₃O₂ is 1.8 × 10^-5.

pH=pKa+log([HA][A−]​)

Where:

• [A⁻] is the concentration of the conjugate base (acetate ion, C₂H₃O₂⁻, from KC₂H₃O₂).

• [HA] is the concentration of the weak acid (HC₂H₃O₂).

• pKa is the negative logarithm of Ka.

Step 2: Calculate pKa

Given Ka for acetic acid (HC₂H₃O₂) is 1.8 × 10⁻⁵:

pKa=−log⁡(1.8×10−5)≈4.74

pKa=−log(1.8×10−5)≈4.74

Step 3: Plug Values into the Henderson-Hasselbalch Equation

Given concentrations:

• [HA] = 0.225 M (from HC₂H₃O₂)

• [A⁻] = 0.162 M (from KC₂H₃O₂)

Now apply the values:

pH=4.74+log⁡(0.1620.225)

pH=4.74+log(0.2250.162​)

pH=4.74+log⁡(0.72)

ph = 4.74 + (-0.143)

pH = 4.60

Compare the effect on pH of adding 0.010 mol NaOH to a buffer that has 0.100 mol HC₂H₃O₂ and 0.100 mol NaC₂H₃O₂ in 1.00 L to adding 0.010 mol NaOH  to 1.00 L of pure water?

See image,

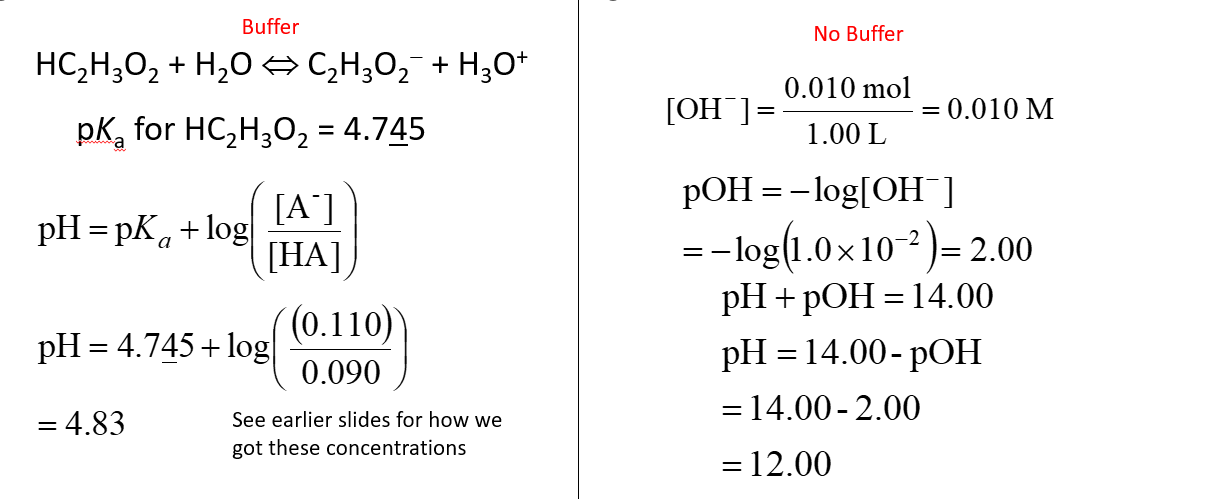
what is buffering range?

the pH Range that the buffer can be effective.

what is the buffering capacity

the amount of acid or base a buffer can neutralize

Which of the following acids would be the best choice to combine with its sodium salt to make a buffer with pH 4.25?

chlorous acid pKa=1.95

nitrous acid pKa=3.34

formic acid pKa=3.74

hypochlorous acid pKa=7.54

To determine which acid would be the best choice for creating a buffer with a pH of 4.25, we need to refer to the Henderson-Hasselbalch equation:

pH=pKa+log⁡([A−][HA])

Where:

• pKa is the acid dissociation constant of the acid.

• [A⁻] is the concentration of the conjugate base (the salt form of the acid).

• [HA] is the concentration of the weak acid.

For a buffer, the pKa of the acid should be close to the desired pH. Ideally, the pKa should be within 1 unit of the target pH, as the buffer works best when the pH is near the pKa.

The best choice to create a buffer with pH 4.25 is formic acid (pKa = 3.74). It is the acid with the pKa closest to 4.25, making it the most suitable for this purpose.

what is the solution of unknown concentration in titrations known as?

titrant

when is a titration complete?

when the moles of H3O+=OH-

what is the difference between solving titrations between buffer problems and ice problems

Key Differences:

1. Approach:

   • Buffer Problems: Focuses on the resistance to pH change in a solution containing a weak acid and its conjugate base, often using the Henderson-Hasselbalch equation.

   • ICE Problems: Focuses on calculating equilibrium concentrations and pH after reactions (such as acid dissociation or neutralization) based on initial concentrations and equilibrium constants.

2. Reaction Type:

   • Buffer Problems: You are primarily concerned with how the buffer components interact with the added acid/base to maintain a relatively constant pH.

   • ICE Problems: You are solving for equilibrium concentrations of species in a dissociation or neutralization reaction (often during a titration) and may involve the full stoichiometry of the neutralization process.

3. pH Calculation:

   • Buffer Problems: Use the Henderson-Hasselbalch equation to calculate pH after adding acid or base.

   • ICE Problems: Set up an ICE table to determine equilibrium concentrations and then use those to calculate pH based on either [H⁺] (for acids) or [OH⁻] (for bases).

In Titration:

• Buffer: You calculate pH changes as a result of acid/base addition to a buffer solution using the Henderson-Hasselbalch equation.

• ICE: You calculate pH changes during a titration (such as titrating a weak acid with a strong base) using stoichiometry and equilibrium constants to find the concentrations of acid/base at different stages of the titration.

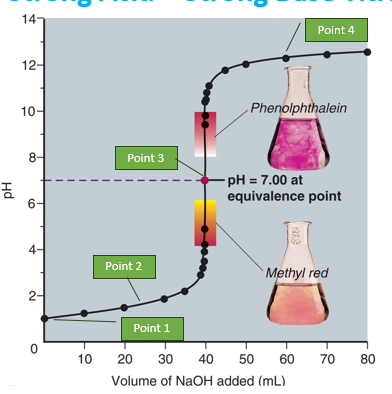
strong acid + strong base titration graph

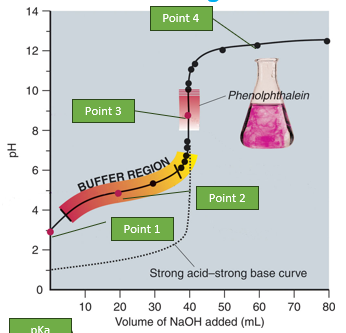
weak acid and strong base titration graph

weak base plus strong acid titration graph

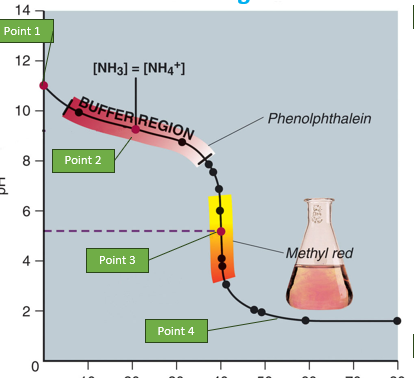
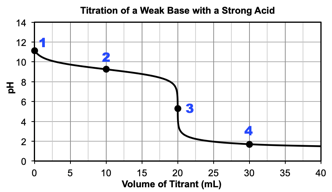
based on the graph were is the buffer region

Titration of a weak base with a strong acid

2

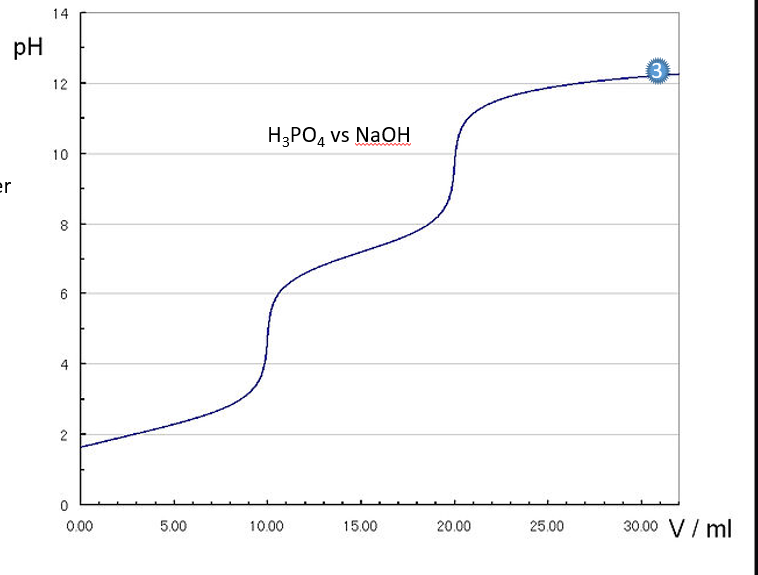
Estimate

•Equivalence point 1

•Equivalence point 2

•Equivalence point 3

•pK_a1,pK_a2,pK_a3

•K_a1,K_a2,K_a3

Label or Write

•Buffer region

Summary of Key Points:

• Equivalence Points: Found at the steep vertical regions of the titration curve (pH jumps). You can estimate the mL of NaOH added at these points.

• Buffer Regions: Found between equivalence points, characterized by gradual pH changes. The pKa values are roughly in the middle of these regions.

• pKa Values: Estimated from the midpoints of buffer regions.

• Ka Values: Calculated as Ka=10−pKa\text{Ka} = 10^{-\text{pKa}}Ka=10−pKa.

Example:

If the graph shows the following pH jumps:

• First equivalence point at 10 mL, pH ~ 5.

• Second equivalence point at 20 mL, pH ~ 9.

• Third equivalence point at 30 mL, pH ~ 12.

Then:

• pKa1 is around pH 2.5–3.5 (halfway between 0 and 10 mL).

• pKa2 is around pH 7.5–8.5 (halfway between 10 and 20 mL).

• pKa3 is around pH 11 (halfway between 20 and 30 mL).

Finally, you can calculate the Ka values as:

• Ka1 ≈ =}10^−pKa1

• Ka2 ≈ 10^−pKa2

• Ka3 ≈ =10^−pKa3