4.3 Fundamentals of algorithms

Explain the basic principle of a depth-first search and give two uses

- each branch of the graph is fully explored (left to right) before backtracking to fully explore the next branch

- uses: maze navigation, detecting cycles in graphs

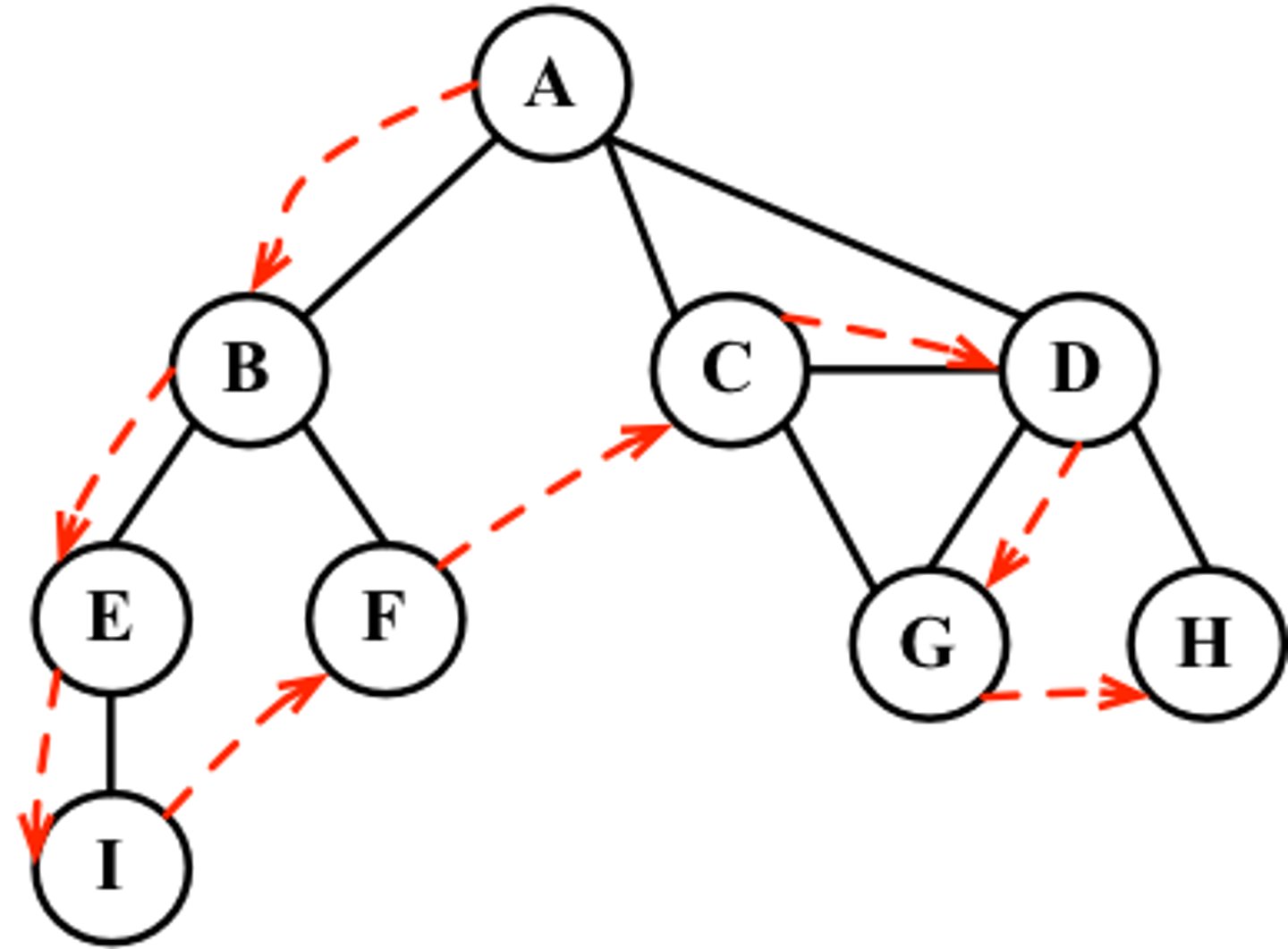
Explain how a stack is used to implement a depth-first search

- add the first node (e.g. the root of a rooted tree) to the result and push onto the stack (using A from diagram)

- observe the nodes that A has a direct connection to (B, C, D) and push the highest alphabetical node onto the stack

- repeat this process for B until the branch is completely explored at I

- when the end of a branch is reached (e.g. at I, F, G, H) then POP THIS node off the stack (backtrack to the previous node) and explore other undiscovered adjacent nodes

- process continues until the stack is empty (NOT when the last node has been discovered, as that whole branch will need to be popped off the stack, so we always backtrack back to the first node

- return the result (probably a list)

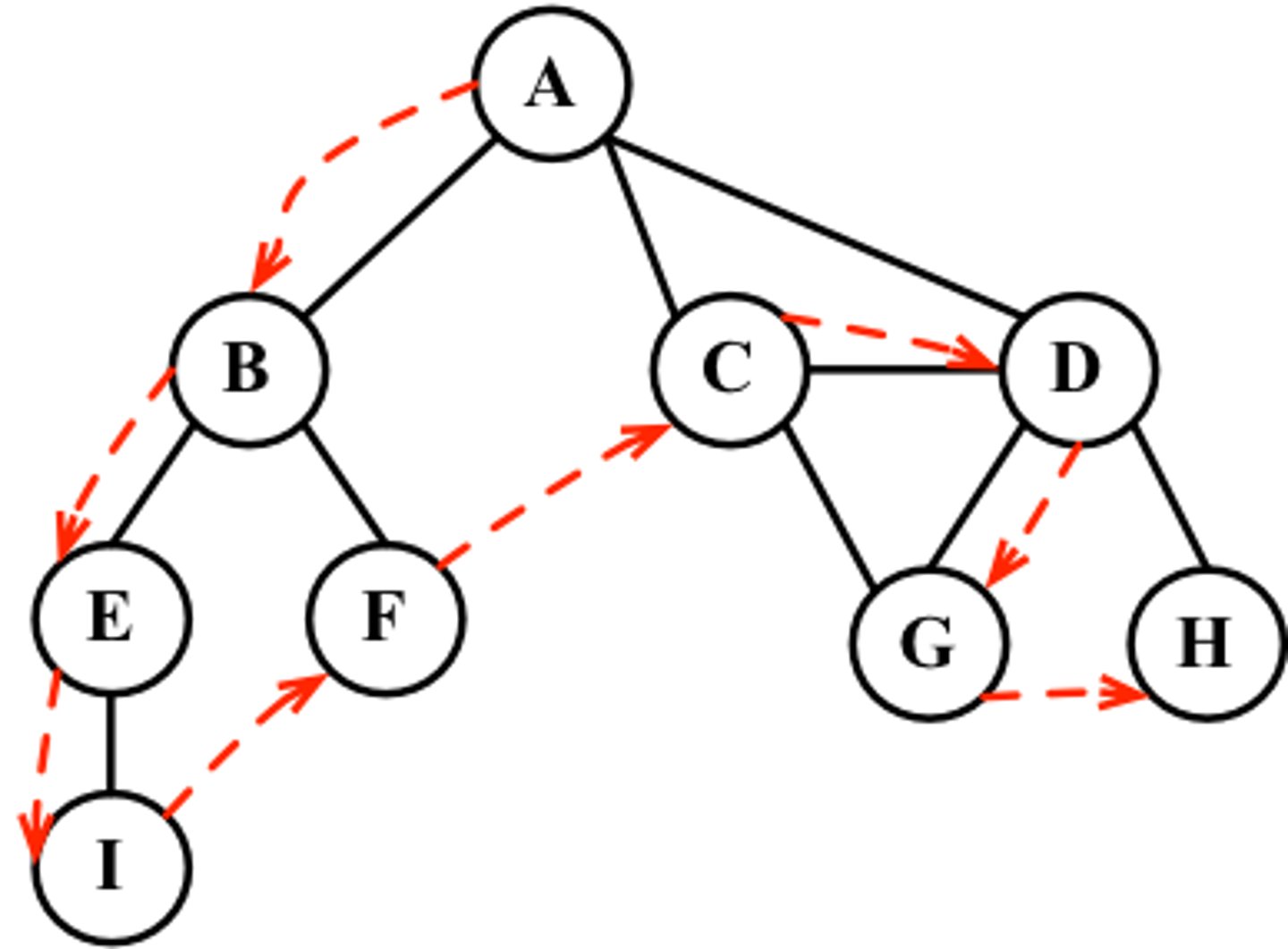
Explain the basic principle of breadth-first search and give two uses

- each node in the graph is fully explored before moving on to the next node

(- a node is considered fully explored when all of its neighbours have been completely explored)

- uses: shortest path for an unweighted graph, level order traversal to generate hierarchal charts

Explain how a queue is used to implement a breadth-first search

- add to starting node (e.g. the root of a tree) TO THE RESULT (here, A) and enqueue ADJACENT nodes in alphabetic order (B, C, D)

- whenever a node is enqueued add it to the result (order of visited)

- the start node is inherently always completely explored after the first step

- dequeue the node at the front of the queue (B) and add its undiscovered nodes to the queue (E, F)

-> example queue state here: C, D, E, F

- repeat this process (if a node has no undiscovered nodes i.e. on the bottom level it is immediately completely explored and process repeats)

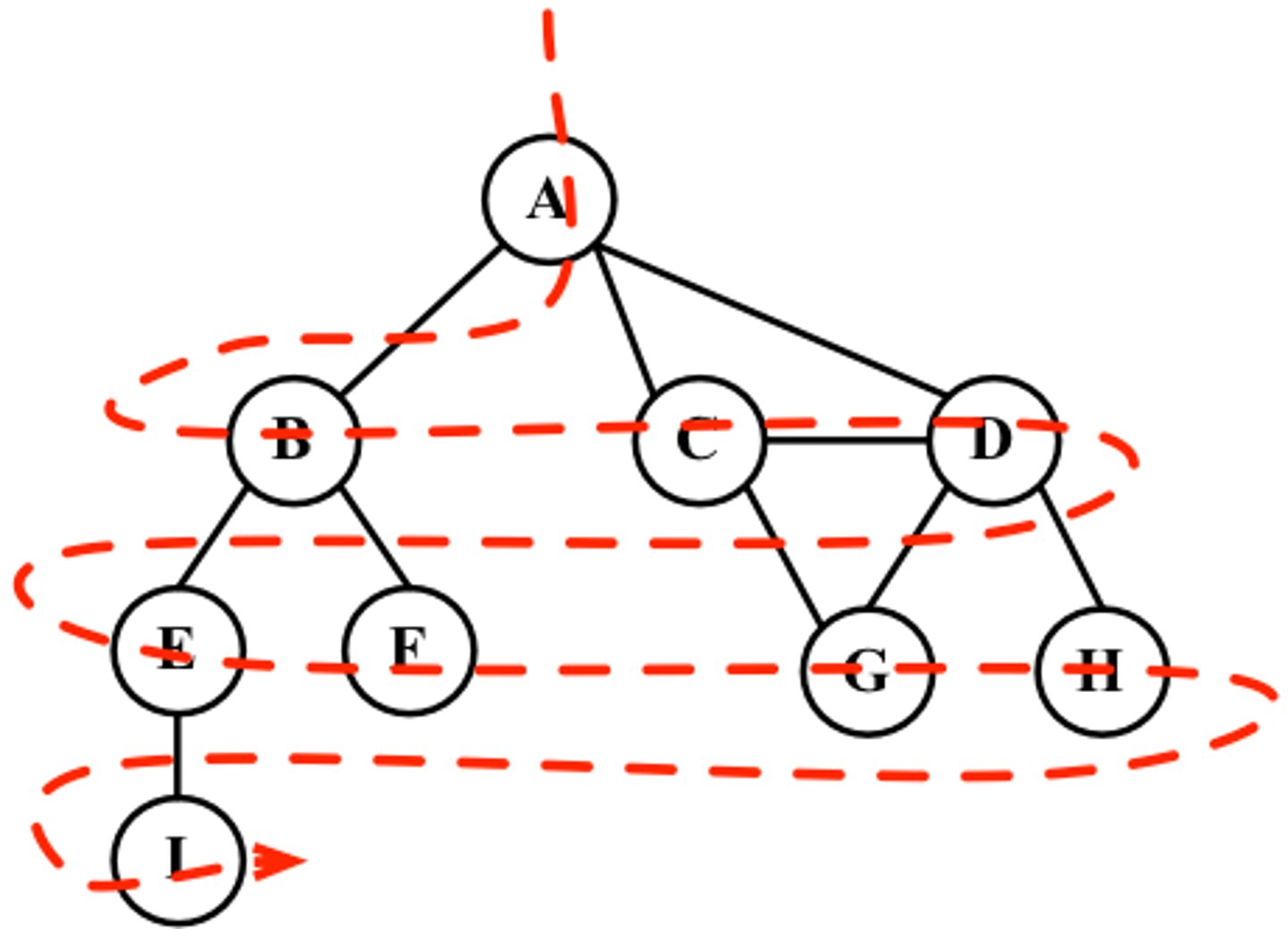
Pre order traversal and use

- LEFT of the line around the nodes

(root, left, right)

-use: copying a tree, task scheduling

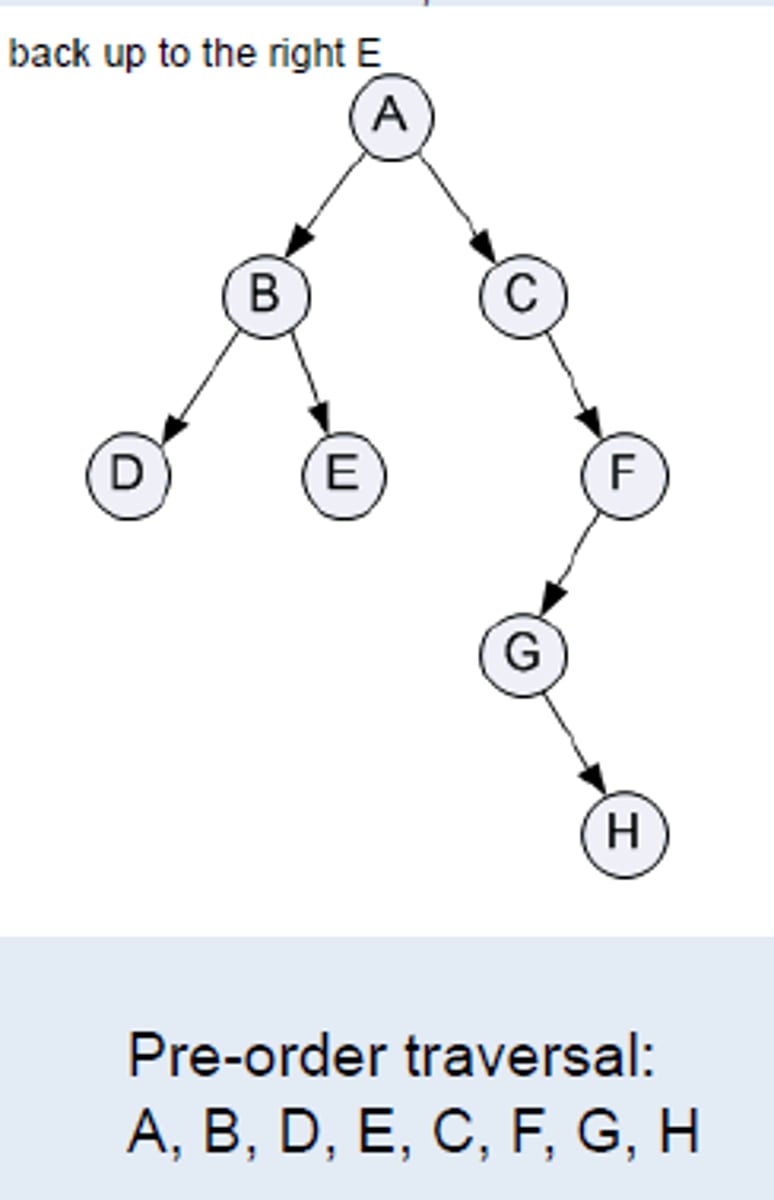
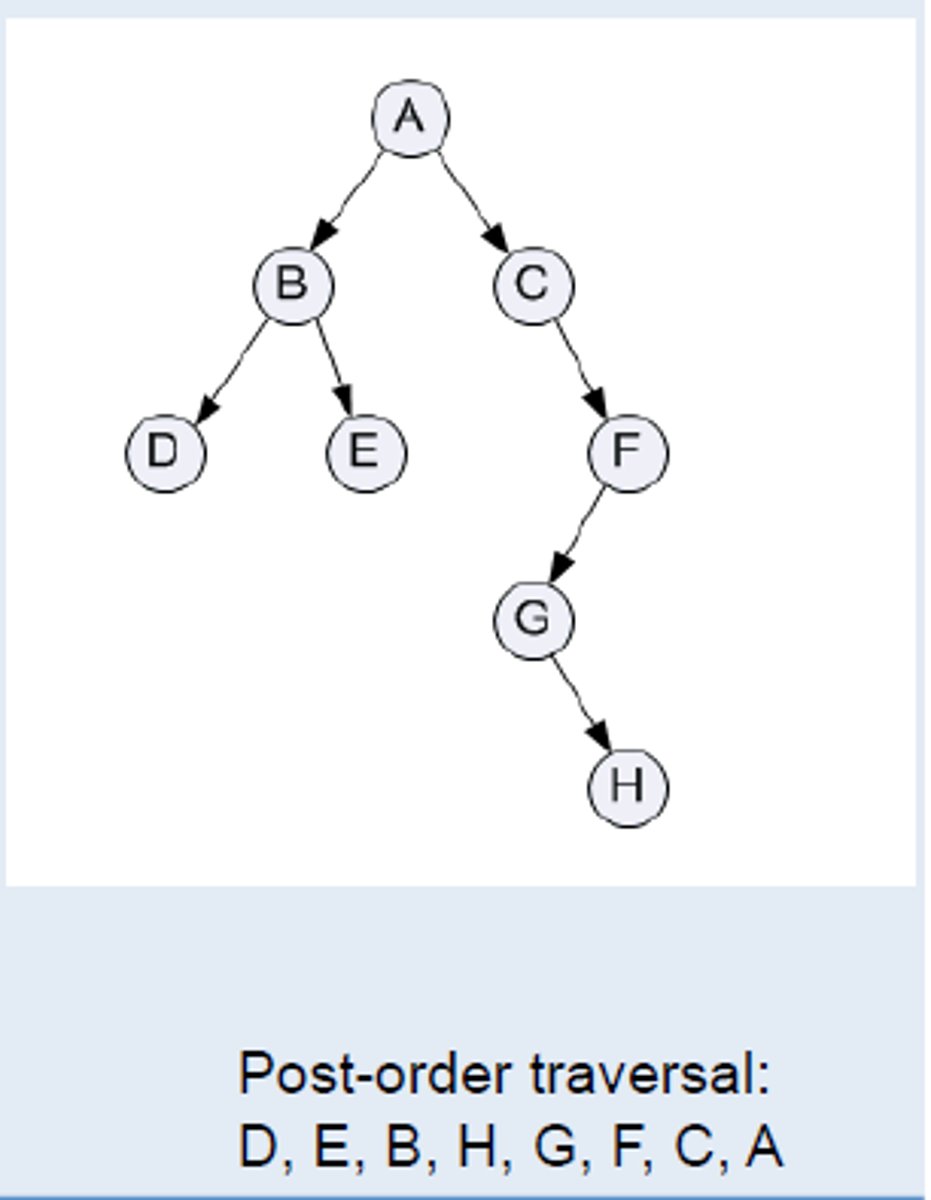
Post order traversal

- RIGHT of the line around the nodes

(left, right, root)

-use: producing postfix (RPN) from an expression tree, emptyting a tree with no backtracking

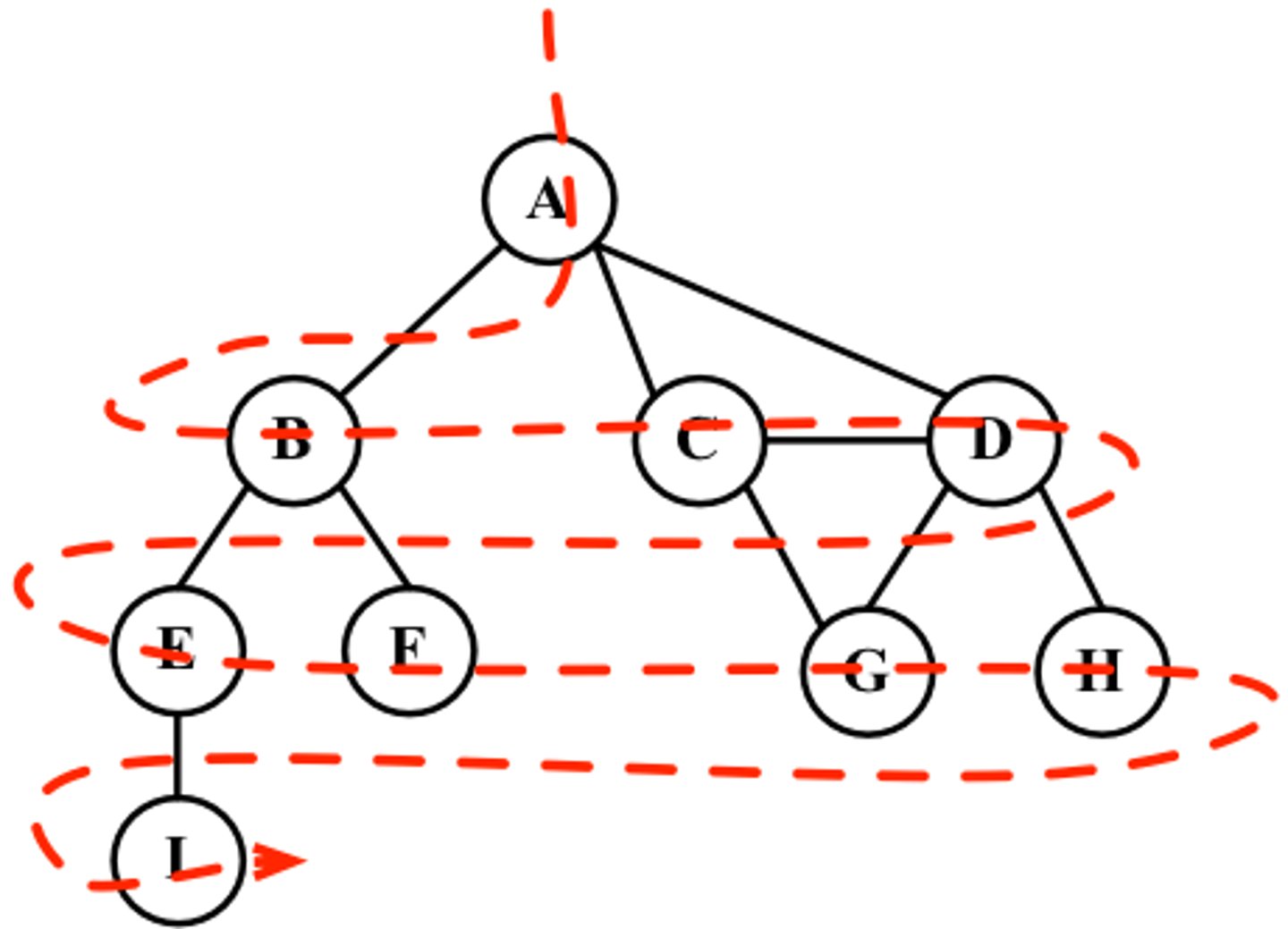
In order traversal

- when the line hits the BOTTOM of each node

- uses: binary search tree (ouputs contents in ascending order) -> can only be used on binary trees

Remember when converting infix to RPN

- conversion via post-order traversal of expression tree

- the order of the numbers must stay the same

Explain how a stack can be used to evaluate RPN

- initialise an empty stack

- read the RPN left to right sequentially:

-> if an operand is encountered then push it onto the stack

-> if an opcode (e.g. +) is read then pop 2 elements from the top of the stack, perform the operation with the element popped second first in sequence, and push the result back onto the stack

- repeat until stack contains only one element - the evaluated RPN

Advantages of using RPN over infix

- no need for parentheses as order of operations is implicitly expressed

-> removes ambiguity

- simple algorithm (easy) for computer to evaluate using a stack due to no backtracking

Where is RPN used in practice?

- in interpreters based on stack functions, e.g. Postscript, bytecode

- in spreadsheets to evaluate user inputs without needing to handle order of operation parsing