12-02: Derivatives
Derivative Rules

IROC: a derivative
In essence, the steps to differentiating (from above)
==Power Rule==
Drop the exponent’s value down to the front of the term
Subtract 1 from the exponent
- If there is a coefficient, then multiply the dropped value by the coefficient
- If you have an exponent of 0, the term is 1 (anything to the power of 0 is 1)
Rational (Radicals) and Negative Exponents:
- To differentiate radicals: express it as a power with a rational exponent
- To differentiate a power of x that is in the denominator: express as a power with a negative exponent
Determining equations from equations
- Find tangent point (if given x value use that to find y by subbing into the original equation)
- Find the derivative
- Sub x value into the derivative to find the slope of the tangent
- Use y=mx+b, plug in (x,y) from tangent point and slope - isolate for b
The Product Rule
Instead of expanding out, there is another way to find the derivative of p(x)=f(x)g(x)
p’(x) = f’(x)g(x) + g’(x)f(x)
The Quotient Rule
Method used to differentiate functions in the form q(x) = f(x)/g(x)
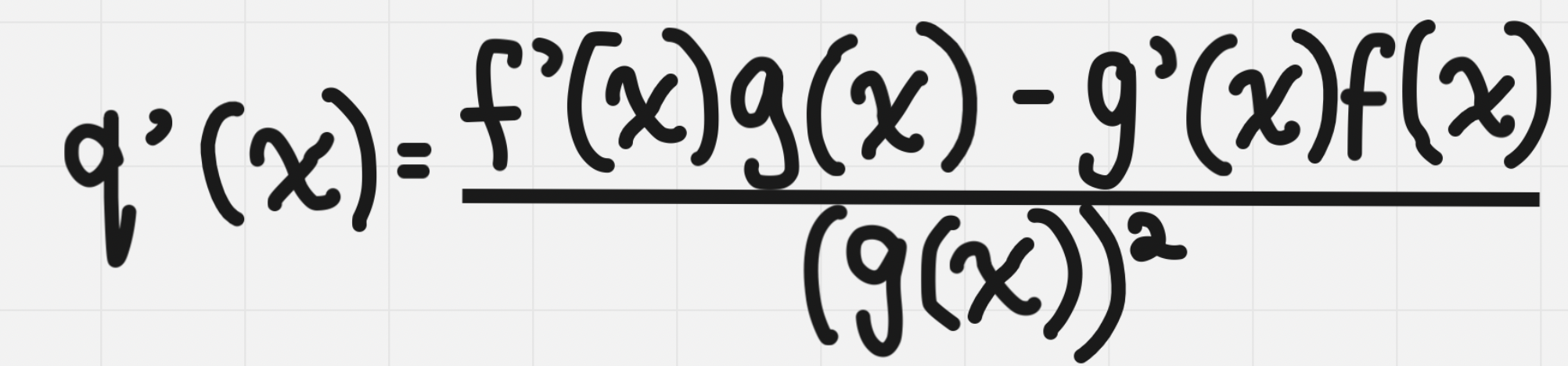
The Chain Rule
Composite function: one function being subbed into another function
- What’s on the inside of the brackets/radical/etc
- Parent function (what’s on the outside)
The chain rule:
f’(x) = g’(h(x)) • h’(x)
- A composite function g(h(x)) consists of an outer function g(x) and an inner function h(x). The chain rule is an effective way of differentiating a composite function by first: differentiating the outer function with respect to the inner function, then multiplying by the derivative of the function
Velocity, Acceleration, and Second Derivatives
Second Derivatives
Second derivative: f’’(x) determined by differentiating the first derivative (same process, just starting from the first derivative)
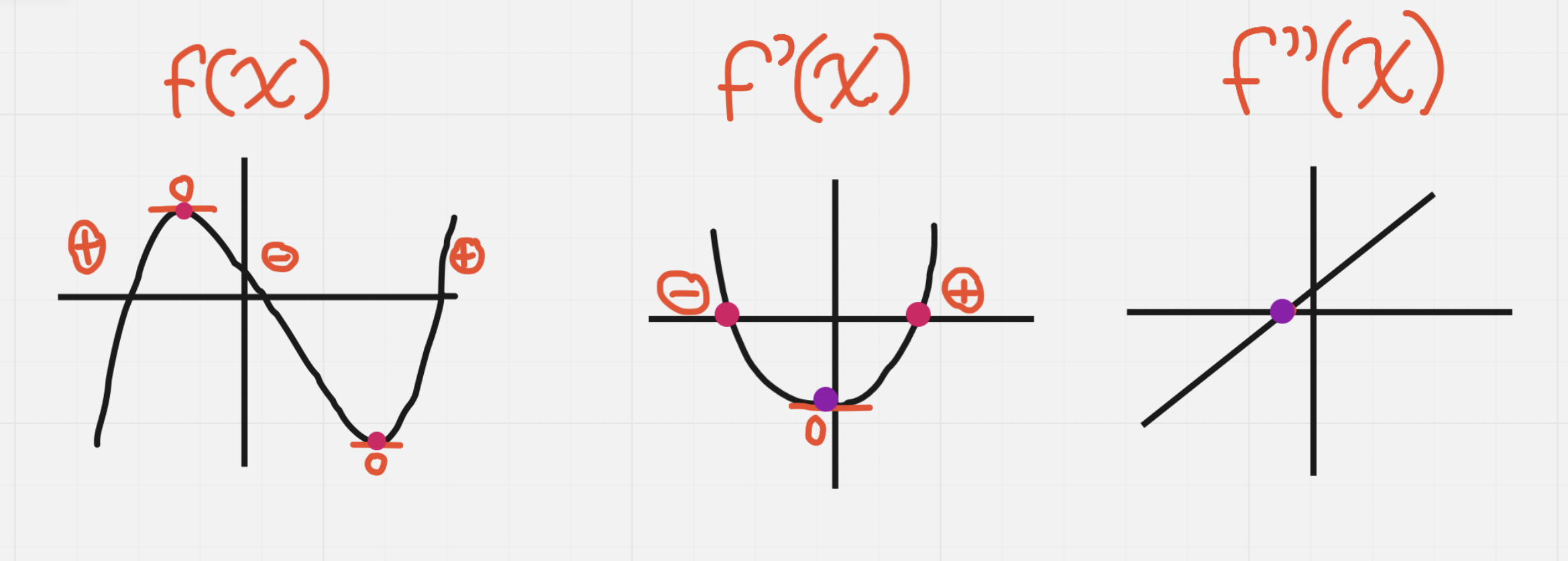
On a graph:
| Slope of f(x) | Derivative |
|---|---|
| + | is +, above x axis |
| 0 | is an x intercept |
| - | is -, below x axis |
| Slope of f’(x) | Derivative |
|---|---|
| + | is +, above x axis |
| 0 | is an x intercept |
| - | is -, below x axis |
Using Derivatives to Analyze the Motion of Objects Travelling in a Straight Line
| Displacement | Velocity | Acceleration | |
|---|---|---|---|
| Definition | Distance and direction that an object has moved from an origin over a period of time | rate of change of displacement of an object with respect to time | rate of change of velocity with respect to time |
| Relationship | s(t) | s’(t) | s”(t) |
| Possible Units | m | m/s | m/s² |
Speed and velocity are different
- Speed: a quantity or scale that describes the magnitude of motion but does not describe direction
- Velocity: a vector quantity with both magnitude and direction
- Answer for velocity questions can be either + or - and the sign indicates the direction at which the object is travelling
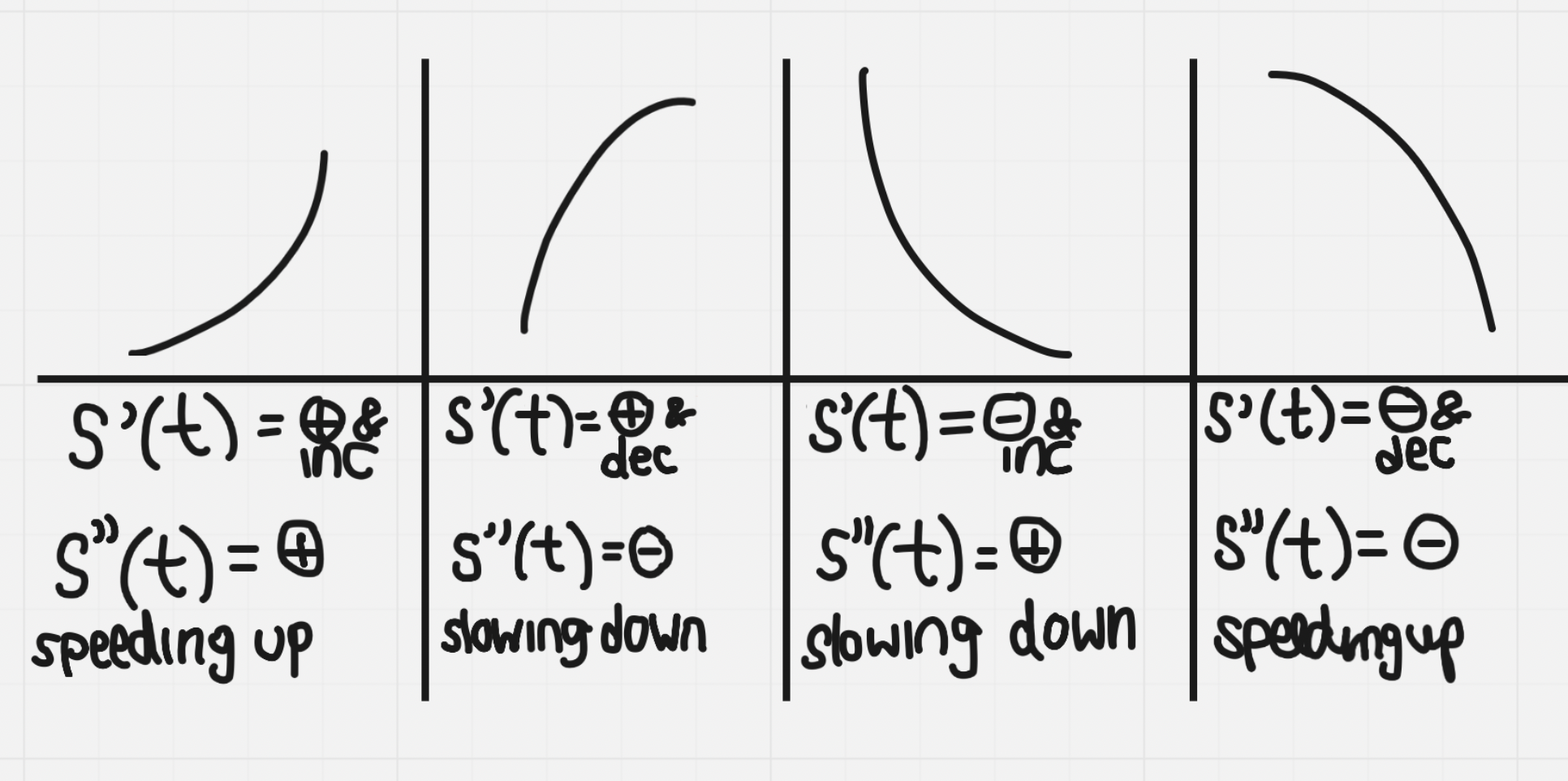
Possible velocity v(t) and acceleration a(t) values:
when v(t) = 0: object is at rest
when v(t) > 0: object is moving in a + direction
when v(t) < 0: object is moving in a - direction
when a(t) > 0: object is accelerating; velocity is increasing
when a(t) < 0: object is decelerating; velocity is decreasing
if v(t) • a(t) > 0: object is speeding up
if v(t) • a(t) > 0: object is slowing down