Optimisation discrète chapitre 1 : THÉORIE DES GRAPHES

Qu’est-ce q’un graphe orienté ?

Un graphe orienté G = (X, U) est un couple formé :

• D’un ensemble X dénombrable de sommets (points, noeuds…)

• famille U ⊂ X × X d’arcs

Qu’est-ce qu’un graphe simple ?

Un graphe sans arcs multiples et sans boucles.

Qu’est-ce qu’un graphe non orienté ?

Un graphe non orinté G = (X, U) est un couple formé d’un ensemble dénombrable de sommets et d’une famille U de paires de sommets, on parle ici d’arrêtes et non d’arcs

On note l’arrête entre deux points x et y : {x; y} ou {y; x}

Compléter la phrase :

• pour une arrête x—y, on dit que x et y sont …….

• L’arrête xy est … à x et à y

• Pour un arc x→y, on dit que x … y et que y …. x

• pour une arrête x—y, on dit que x et y sont voisins adjacents

• L’arrête xy est incidente à x et à y

• Pour un arc x→y, on dit que x précède y et que y est le successeur de x

Dans quel cas x et y sont à la fois successeurs et prédécesseurs ?

x ⇌ y

Qu’est-ce qu’un degré/demi degré pour un sommet x : d(x) ?

Pour un sommet x son demi degré :

• Intérieur est le nombre d’arcs incidents intérieurement à x d^-(x)

• Extérieur est le nombre d’arcs incidents extérieurement à x d⁺(x)

  d(x) = d^-(x) + d⁺(x)

Que note-t’on : δ(x) ?

On note :

• δ⁺(x) est l’ensemble des arcs incidents extérieurement à x.

• δ^-(x) est l’ensemble des arcs incidents intérieurement à x.

• δ(x) = δ⁺(x) ⋃ δ^-(x)

Que note-t’on ρ(x)

On note :

• ρ⁺(x) est l’ensemble des sommets successeurs de x.

• ρ^-(x) est l’ensemble des sommets prédécesseurs de x.

• ρ(x) = ρ⁺(x) ⋃ ρ^-(x) (ensemble des sommets adjacents/voisins d à x)

Donner le lien entre les cardinaux de pour (d(x) et…)

• d⁺(x) = |ρ⁺(x)| = |δ⁺(x)|

• d^-(x)= |δ^-(x)| = |ρ^-(x)|

• d(x)= |δ(x)| = |ρ^-(x)|

Compléter ce théorème :

Soit G = (X,U) un graphe non orienté, alors le nombre de sommets de degré … est …

Soit G = (X,U) un graphe non orienté, alors le nombre de sommets de degré impairs est pair

Donner la démonstration de :

Soit G = (X,U) un graphe non orienté, alors le nombre de sommets de degré impairs est pair

Que dit-on quand deux graphes sont isomorphes ?

Deux graphe G₁ = (X₁ , U₁) et G₂ = (X₂ , U₂) sont isomorphes ssi il existe une bijection f : X₁ → X₂ telle que ∀ i, j ∈ X₁, ij ∈ U₁ ⟺ f(i)f(j) ∈ U₂

Qu’est-ce qu’un sous graphe engendré par X’ ?

Soit G = (X, U) un graphe X’ ⊂ X

Le sous graphe induit/engendré par X’ est le graphe G’ = (X’, U’) avec U’ l’ensemble des arcs ou arrêtes de U entre des extrémités qui sont dans X’

Qu’est-ce qu’un graphe partiel engendré par U ?

Soit G = (X, U) un graphe U’ ⊂ U

Le grape partiel induit/engendré par U’ est le graphe G’ = (X, U’)

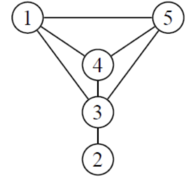
Donner

• le Laplacien de ce graphe

• sa matrice adjacente

• la liste de ses arrêtes

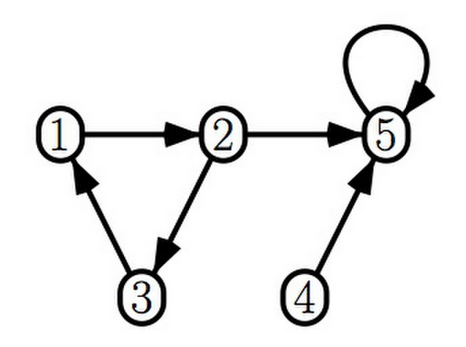
• Pourquoi n’y a til pas de laplacien de graphe ?

• sa matrice adjacente

• la liste de ses arrêtes

• la liste predécesseurs et successeurs de 1,3,4

• EN OUBLIANT LA BOUCLE A 5, donner la matrice d’incidence de ce graphe

Car c’est un graphe orienté

Compléter la phrase : Une matrice d’incidence B vérifie : ……. ≤ ……. (avec …..) car la …… des lignes est …… par définition.

Une matrice d’incidence B vérifie : rang(B) ≤ n-1 (avec n le nombre de sommets ) car la somme des lignes est nulle par définition.

Qu'est-ce qu'un chemin p dans un graphe simple orienté G ?

Donner l’une des trois définitions

1. Un chemin p dans G est une suite finie décomposée simple i₀, i₁, ..., iₚ telle que (p ≥ 1) ∀k ∈ {0, ..., p-1}, (iₖ, iₖ₊₁) ∈ U

2. Un chemin p dans G est une suite finie d’arcs (i₀, i₁), (i₁, i₂), …, (iₚ₋₁, iₚ)

3. Un chemin p dans G est une suite finie d’arcs u₁, …, uₚ telle que l’extrémité finale d’un arc uₖ (1 ≤ k ≤ p-1) et l’extrémité initiale de l’arc uₖ₊₁ coïncident

Qu’est-ce qu’une chaîne dans un graphe simple non orienté G ?

1. Un chaîne entre s et t (avec s et t ∈ X)  dans G est une suite finie d’arêtes i₀, i₁, ..., iₚ telle que (p ≥ 1) ∀k ∈ {0, ..., p-1}, (iₖ, iₖ₊₁) ∈ U, avec i₀ = s et i_p = t.

Quand dit-on qu'un chemin est un circuit ?

Si i₀ = iₚ, le chemin est un circuit

Qu'est-ce qu'une chaîne dans un graphe non orienté?

Dans un graphe orienté, une chaîne est une suite finie de sommets i₀, i₁, ..., iₙ telle que pour chaque k (0 ≤ k < n), l'ar^ete (iₖ, iₖ₊₁) existe dans le graphe.

Qu'est-ce qu'un cycle dans un graphe non orienté ?

Une chaîne dont les sommets de départ et d'arrivée sont les mêmes est un cycle.

Quand dit-on qu'un graphe orienté est fortement connexe ?

Un graphe G = (X, V) orienté est fortement connexe ssi ∀x, y ∈ X (x ≠ y) ou (il existe un chemin de x à y) et (il existe un chemin de y à x)

Quand dit-on qu'un graphe non orienté est connexe ?

Un graphe G = (X, V) est connexe ssi ∀x, y ∈ X (x ≠ y) (il existe une chaîne entre x et y)

Quelle est la relation entre la forte connexité et la connexité ?

La forte connexité entraîne la connexité.

Comment est définie la relation R (relation de connexité) ?

La relation R est définie par : ∀x, y ∈ X, x R y ssi (x = y) ou (il existe une chaîne entre x et y).

Démontrer la propriété suivante : La relation R est une relation d'équivalence.

Réflexivité : ∀x ∈ X, x R x

Symétrie : x R y ⇔ y R x

Transitivité : x R y et y R z ⇒ x R z

Comment sont appelées les classes d’équivalences de R ?

Les classes d’équivalence de R sont appelées composantes connexes du graphe.

Quelle est la propriété de la relation R’ (relation de forte connexité)?

La relation R’ (relation de forte connexité) est définie par : ∀x, y ∈ X, x R y ssi (x = y) ou (un chemin de x à y est un chemin de y à x).

Comment définit-on un graphe réduit ?

On appelle graphe réduit du graphe G = (X, U) le graphe Gᵣ = (Xᵣ, Uᵣ), où l'ensemble des sommets Xᵣ est en bijection avec l'ensemble des composantes fortement connexes de G

{C₁, …, C_p} et C_iC_j ∈ U_R ⇔ Il existe un arc partant d’un sommet de C_i vers un sommet de C_j

Quelle est la propriété d'un graphe réduit ?

Un graphe réduit n'a pas de circuit (sauf éventuellement des boucles), c'est-à-dire qu'il ne peut pas exister 2 sommets de la même classe d'équivalence Cᵢ et Cⱼ formant un circuit.

Qu'est-ce que la fermeture transitive d'un graphe ?

La fermeture transitive de G est le graphe τ(G) = (X, τ(U)) où ∀xy ∈ τ(U) ⇔ il existe un chemin de x vers y dans G.

Quand dit-on que deux graphes G₁ et G₂ sont τ-équivalents ?

G₁ et G₂ sont τ-équivalents s'ils ont la même fermeture transitive.

Qu'est-ce qu'un graphe τ-minimal ?

Un graphe G = (X, U) est τ-minimal ⇔ ∀u ∈ U, τ(G) ≠ τ(G - {u}).

Compléter ce théorème :

Si G est un ……, alors le graphe τ-minimal est …….

Théorème : Si G est un sous circuit, alors le graphe τ-minimal est unique.

Compléter cette remarque:

Théorème : Si G = (X, U) est …., alors la matrice d'adjacence H de τ(C(G)) a des …. partout sauf sur ……..

Remarque : Si G = (X, U) est fortement connexe, alors la matrice d'adjacence H de τ(G) a des 1 partout sauf sur la diagonale.

Compléter ce théorème :

Théorème : G = (X, U) est ……………… ssi ∀A ⊆ X, A ≠ ∅, A ≠ X, on a ……… et …………...

Théorème : G = (X, U) est fortement connexe ssi ∀A ⊂ X, A ≠ ∅, A ≠ X, on a τ⁺(A) ≠ A et τ⁺(A) = ∪_x∈A τ⁺({x}).

Donner la démonstration de :

G = (X, U) est fortement connexe ssi ∀A ⊂ X, A ≠ ∅, A ≠ X, on a τ⁺(A) ≠ A et τ⁺(A) = ∪_x∈A τ⁺({x}).

Soit A ≠ ∅, X, A ⊂ X tel que Γ⁺(A) = A. Considérons y ∉ A : il n’existe pas de chemin d’un point de A à y, ce qui contredit la forte connexité.

Qu'est-ce qu'un arbre ?

Un arbre est un graphe connexe sans cycle.

Qu'est-ce qu'une feuille (ou sommet pendant) ?

Une feuille (ou sommet pendant) est un sommet de degré 1.

Qu'est-ce qu'une forêt ?

Une forêt est un graphe dont les composantes connexes sont des arbres.

Compléter cette propriété :

De façon équivalente, ……… est un graphe …….

De façon équivalente, une forêt est un graphe sans cycle.

Quelles sont les propositions équivalentes pour un graphe T = (X, U) avec |X| = n ?

1. T est un arbre (graphe connexe sans cycle)

2. Deux sommets quelconques de T sont joints par une chaîne unique

3. T est connexe et si on supprime une arête, le graphe n'est plus connexe

4. T est connexe et |U| = n - 1

5. T est sans cycle et |U| = n - 1

6. T est sans cycle et en ajoutant une arête, on crée un cycle et un seul

Compléter ce théorème sur les arbres :

Un arbre a ……. pour ……...

Un arbre a au moins 2 feuilles pour n ≥ 2.

Doner la démonstration du thorème : Un arbre a au moins 2 feuilles pour n ≥ 2

Soit T = (X, U) un arbre, n = |X| et m = |U| = n - 1.

∑_x∈X d(x) = 2|U| = 2n- 2.

Si tous les sommets sont de degré ≥ 2 : ∑_x∈X d(x) = 2n > 2n - 2.

S’il y a un seul sommet de degré 1 et les autres de degré ≥ 2 : ∑_x∈X d(x) = 2n - 1 > 2n - 2.

Donc il y a forcément au moins 2 sommets de degré 1 (au moins 2 feuilles).

Compléter ce théorème :

G admet un ……….. qui est un ………⇔ G est …….

G admet un graphe partiel qui est un arbre ⇔ G est connexe.

Donner la démonstration de : Si T est un arbre et le graphe partiel engendré par G, alors G est connexe

Sens direct :

Soit T = (X, U’), G = (X, U) avec U’ ⊂ U.
Si T est un arbre, alors entre deux sommets quelconques, il y a une chaîne.
Donc G est connexe.

Réciproque :

S’il n’y a pas de cycle, alors c’est un arbre (U’ = U).

S’il y a un cycle, on peut supprimer une arête en conservant la connexité.
On continue jusqu’à ce qu’il n’y ait plus de cycle.

Qu’est-ce qu'un arbre couvrant?

Soit G = (X, U) connexe et T un graphe partiel de G qui est un arbre.
Alors T est dit arbre couvrant.

Qu’est-ce qu’une racine d’un graphe orienté G = (X, U) ?

Une racine du graphe G(X, U) oriente est un sommet r tel que tout autre sommet de G peut être atteint par un chemin issu de r.

Est-ce qu’un graphe orienté possède toujours une racine ?

Non, il n’y a pas forcément de racines.

Quand dit-on qu’un graphe est quasi fortement connexe ?

Un graphe est quasi fortement connexe si, pour tout couple (x, y) de sommets distincts, il existe un sommet z ≠ x, y d’où part à la fois un chemin vers x et un chemin vers y.

Quelle est la relation entre forte connexité et quasi forte connexité ?

La forte connexité entraîne la quasi forte connexité.

Quelle est la relation entre quasi forte connexité et connexité ?

La quasi forte connexité entraîne la connexité.

Qu’est-ce qu’une arborescence ?

Une arborescence est un arbre muni d’une racine, c’est-à-dire un graphe orienté connexe sans cycle avec une racine.

Donne un exemple d’arborescence

L’arborescence des descendants scientifiques de Leibniz (exemple : Leibniz → Jacobi → Michel Amacourt → …).

Quelle est la propriété reliant racine et quasi forte connexité ?

G = (X, U) admet une racine ⇔ G est quasi fortement connexe.

Comment montrer que si G a une racine r, alors G est quasi fortement connexe ? Et montrer la réciproque

Supposons que G a une racine, on veut montrer que G est quasi fortement connexe

Si r est racine, alors pour tout couple (x, y) de sommets distincts, r est un sommet d’où part un chemin vers x et un chemin vers y.

G est quasi fortement connexe, montrons que G a une racine

À partir d’un couple (x₁, x₂), on peut construire une suite de sommets reliant progressivement tous les autres. On obtient ainsi un sommet r qui est une racine.

Comment montrer que G est quasi fortement connexe ssi il admet une racine ?

À partir d’un couple (x₁, x₂), on peut construire une suite de sommets reliant progressivement tous les autres. On obtient ainsi un sommet r qui est une racine.

Théorème (équivalences pour H = (X, U) avec |X| = n)

Les propriétés suivantes sont équivalentes :

a) H est une arborescence.

b) H est quasi fortement connexe et sans cycle.

c) H est un graphe connexe avec |U| = n - 1.

d) Il existe un sommet a relié à tous les autres par un chemin unique issu de a.

e) H est quasi fortement connexe et cette propriété subsiste après suppression d’un arc quelconque.

f) H est connexe et il existe un sommet sans prédécesseur tel que tous les autres sommets ont un unique prédécesseur.

g) H est sans cycle et il existe un sommet sans prédécesseur tel que tous les autres sommets ont un unique prédécesseur.

Qu'est-ce qu'un graphe biparti ?

Définition : Un graphe G = (X,U) est biparti si on peut partitionner l'ensemble X des sommets en deux ensembles non-vides X₁ et X₂ tels que toute arête (ou arc) de U a exactement une extrémité dans X₁ (et donc l'autre dans X₂).

Donne un exemple d’algorithme avec 2 fonctions récursives pour tester si un graphe est biparti.

Exemple : 1 algorithme avec 2 fonctions récursives Choisir un sommet x₀, le colorier en bleu et appeler la fonction : coloration_rouge(x₀)

Fonction Coloration_rouge(sommet x₀) 

Début 

	Pour tout voisin y de x₀ 

		Si y est colorié en bleu//graphe pas biparti 

		Alors fin (on sort de la récursivité) 

		Finsi 

		Si y est non colorié 

			Alors colorier y en rouge

		Finsi 

	Finpour 

Fin

Fonction Coloration_bleu(sommet x₀) 

Début 

	Pour tout voisin y de x₀ 

		Si y est colorié en rouge //graphe pas biparti 

		Alors fin (on sort de la récursivité) 

		Finsi 

		Si y est non colorié 

			Alors colorier y en bleu 

		Finsi 

	Finpour 

Fin

Compléter la propriété

Un graphe est ….. ssi il ne possède pas de…….

Propriétés : Un graphe est biparti ssi il ne possède pas de cycle de longueur impaire.

Qu'est-ce qu'un graphe planaire ? Donner un exemple

Définition : Un graphe G = (X,U) non orienté est planaire si on peut le dessiner sans croisement d’arêtes dans le plan (ou sur une sphère).

Exemple : K₄

Qu’est-ce qu’un graphe plan ?

Définition : Un graphe plan est l’association d’un graphe planaire et d’une représentation de ce graphe dans le plan.

Qu’est-ce qu’une face en théorie des graphes planaires ?

Définition : Une face est une région du plan délimitée par des arêtes.
La face qui s’étend à l’infini est appelée face extérieure.

Qu’est-ce que le graphe dual d’un graphe planaire ?

Définition : Le graphe dual G* d’un graphe G = (X,U) est G* = (F,U*) où chaque sommet de F correspond à une face de la représentation planaire de G, et chaque arête u* de U* correspond à une arête u de U et relie deux faces délimitées par u.

Quelle est la formule d’Euler pour les polyèdres et les graphes planaires connexes ?

Théorème : Formule d’Euler pour les polyèdres et les graphes planaires connexes
n + f = m + 2
avec n = nombre de sommets, f = nombre de faces, m = nombre d’arêtes.

Quelle est la formule d’Euler pour les graphes planaires de p composantes connexes ?

Théorème : Formule d’Euler pour les graphes planaires de p composantes connexes :
n + f = m + p + 1
avec n = nombre de sommets, f = nombre de faces, m = nombre d’arêtes et p = nombre de composantes connexes.

Que dit le corollaire de la formule d’Euler sur les degrés des sommets ?

Dans tout graphe simple planaire G, il existe un sommet x tel que d(x) ≤ 5

Qu’est-ce qu’un mineur d’un graphe G ?

Un mineur d’un graphe G est obtenu par suppression de sommets, d’arcs ou par fusion de sommets (en nb quelconque).

Que signifie la fusion de deux sommets u et v dans un graphe ?

Deux sommets u et v sont fusionnés en les remplaçant par un nouveau sommet z relié aux sommets qui étaient voisins de u ou v.

Quel est le théorème caractérisant les multigraphes planaires (admis) ?

Un multigraphe est planaire ssi il n’a pas de mineur isomorphe à K5 ou K3,3.

Qu'est-ce qu’un graphe eulérien ?

Un graphe G = (X,U) non orienté est eulérien s’il possède un cycle passant exactement une fois par chaque arête.

Quel est le théorème d’Euler (1736) ?

Une condition nécessaire pour qu’un graphe soit eulérien est que tous les sommets soient de degré pair.

Quel est le théorème de Hierholzer (1873) ?

Si G est connexe et si tous les sommets sont de degré pair, alors G est eulérien.

Quel est le théorème sur les circuits eulériens ?

G possède un circuit eulérien ssi G est connexe et ∀x ∈ X, d⁻(x) = d⁺(x).

Qu'est-ce qu'une famille totale ?

Une famille A ⊂ H est dite totale si Vect(A) = H.

Qu'est-ce qu'un cycle hamiltonien ?

Un cycle hamiltonien est un cycle élémentaire de n sommets, c.-à-d. un cycle qui utilise exactement une fois chaque sommet.

Énoncé du théorème sur les circuits eulériens ?

G possède un circuit eulérien ssi G est connexe et ∀x ∈ X, d⁻(x) = d⁺(x).

Qu'est-ce qu'une famille totale ?

Une famille A ⊂ H est dite totale si Vect(A) = H.

Qu'est-ce qu'un cycle hamiltonien ?

Un cycle hamiltonien est un cycle élémentaire de n sommets, c.-à-d. un cycle qui utilise exactement une fois chaque sommet.

Énoncé du théorème sur les circuits eulériens ?

G possède un circuit eulérien ssi G est connexe et ∀x ∈ X, d⁻(x) = d⁺(x).

Définition : Soit G = (X,U) un graphe non orienté. Un ensemble S ⊂ X est dit stable (ou indépendant) si 2 sommets distincts de S ne sont jamais adjacents.

Autrement dit, Γ(S) ∩ S = ∅.

Définition : S₀ est un ensemble stable minimal si ∀S₁ ∈ S, S₁ ≠ S₀, on a S₀ ⊄ S₁ (minimal au sens de l’inclusion).

C’est un stable qu’on ne peut pas réduire tout en restant stable.

Définition : On appelle nombre de stabilité α(G) = max |S| pour S ∈ S.

C’est la taille maximale d’un ensemble stable.

Définition : Un ensemble S ⊂ X tel que |S| = α(G) est dit stable maximum.

C’est un ensemble stable qui atteint la taille maximale possible.

Définition : Une clique de G est un sous-graphe de G qui est complet.

C’est un ensemble de sommets tous reliés entre eux.

Définition : Un support de G = T est un ensemble de sommets tel que toute arête de U a au moins une extrémité en T.

Autrement dit, chaque arête est "couverte" par T.

Définition : Le graphe complémentaire de G est noté G̅ = (X, U̅) avec u ∈ U̅ ⇔ u ∉ U.

Il contient exactement les arêtes qui ne sont pas dans G.

Propriété : Les trois propriétés suivantes sont équivalentes :
1) S est un ensemble stable.
2) S engendre une clique dans G̅.
3) X \ S est un support de G.

Théorème de Berge (1960) : Dans un graphe simple G = (X,U), |X| = m et de degré maximal Δ, tout ensemble stable maximum Sm vérifie :
|Sm| ≥ ⌈ m / (Δ + 1) ⌉ .

Autrement dit, la taille d’un stable maximum est au moins le plus petit entier supérieur ou égal à m / (Δ+1).

Définition : A ⊆ X est absorbant si ∀x ∈ X, Γ⁺(x) ∩ A ≠ ∅.

Un absorbant est un ensemble de sommets qui "couvre" les autres.

Définition : Le nombre d’absorption β(G) = min |A|, A ∈ ℱ.

C’est la taille minimale d’un ensemble absorbant.

Définition : Un absorbant minimum réalise le nombre d’absorption.

C’est un ensemble absorbant de cardinalité β(G).

Définition : Une k-coloration des sommets est une partition de X en k ensembles stables S₁, …, Sₖ.

C’est une façon de colorier les sommets avec k couleurs sans que deux sommets adjacents aient la même couleur.

Définition : Le nombre chromatique de G = (X,U), noté χ(G), est le plus petit nombre de couleurs nécessaires pour colorier les sommets de G, de sorte que deux sommets adjacents soient toujours de couleurs différentes.

χ(G) est le minimum de k pour lequel G est k-colorable.