Midterms - Mathematics in the Modern World

To most of us, the common concept of _ is that it is all about numbers and their operations. The usual reaction is that _ is a difficult subject, disliked, and even hated. However, that concept is just one aspect of _ because it also pertains to a study of patterns, a language, a set of problem-solving tools, a process of thinking, and _ an art.

Mathematics

The regularities that we see in the forms of the things in the natural world.

Patterns in Nature

An imaginary line is drawn across an object, the resulting parts are mirrors of each other.

Symmetry

It is a curved pattern that focuses on a center point and a series of circular shapes that revolve around it. This is common in plants and some animals.

Spiral

Series of regular sinuous curves, bends, loops, turns, or windings in the channel of a river, stream, or other watercourses. It is produced by a stream or river swinging from side to side as it flows across its floodplain or shifts its channel within a valley.

Meander

Linear openings that form in materials to relieve stress. The pattern indicates whether the material is elastic or not.

Cracks

Strip or band that has a different color from the surface surrounding it. This may be seen in various living things, especially animals.

Stripe

Are usually the first to be observed since making categories or classification comes before numeration. For children, these include studying shapes and colors. For older ones, these can be seen on aptitude tests wherein takers are shown a sequence of pictures and asked to select which figure comes next among several choices.

To identify them, look out for four things, namely:

• rotating shapes

• increase and decrease in numbers of shapes or patterns

• alternating patterns, colors, and shapes

• mirror images or reflections

Logical Patterns

Consists of shapes like polygons and circles that are repeated to create a design. They can be seen in nature and in different artworks. Examples of these patterns are also found in textiles, floor tiles, paintings, and wallpapers.

Geometric Patterns

Pattern that is formed by repeating polygons to cover a plane so that there are no gaps or overlaps. It may be regular (where a regular polygon is repeated) or semiregular (with two or more regular polygons being repeated).

Tessellations

A never-ending pattern. It can be formed by continuously repeating something. Because of these continuous repetitions, they are considered to be self-similar. Each part of the object is similar to the whole object. Some famous examples of this are the Sierpinski Triangle, Pascal's Triangle, Koch Snowflake, and Fractal Tree.

Fractals

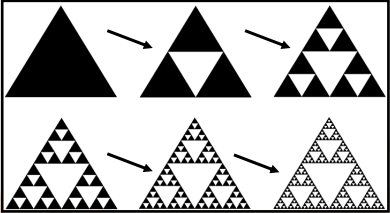
Fractal that is named after the Polish mathematician Waclaw Franciszek Sierpinski. To draw this, start with an equilateral triangle. Mark the midpoint of each side and connect these points. Four triangles are now formed. Repeat the procedures to each of the triangles formed except for the middle triangle.

Sierpinski Triangle

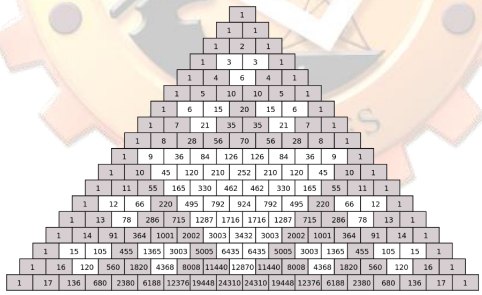
Contains the numerical coefficients of binomial expansions. The triangle below shows the coefficients of (𝑥 + 𝑦)⁰ up to (𝑥 + 𝑦)¹⁷. In this, the Sierpinski triangle can also be drawn by connecting or shading the odd numbers.

Pascal’s Triangle

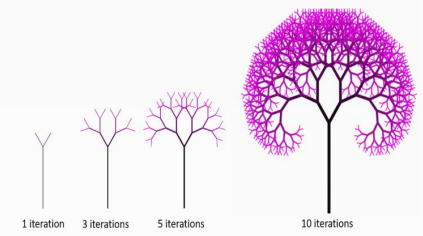
To construct this, start at some point and draw a line segment. From an endpoint, draw two branches at a certain angle. Repeat the previous step to the new endpoints and continue the process to make more branches.

Fractal Tree

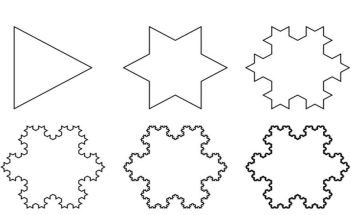
In drawing this, one needs to start by drawing an equilateral triangle. Then, divide each side into three equal parts. After that, draw an equilateral triangle on each middle part. Then divide each outer side into thirds and again, draw an equilateral triangle on the middle part. Repeat until you're satisfied with the number of iterations.

Koch Snowflake

Can be found in giving the plural of nouns, in forming the past tense of verbs, and in word analogy. They can also be found in the meters of poetry and in the rhythm of the words.

Word Patterns

Plural of Nouns

Past Tense of Verbs

Compares two different things, showing the relationship between them. The colons stand for words; single colon reads as “is to”, double colon reads “as”.

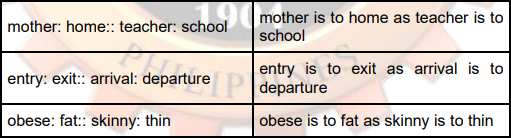
Analogy

The rhymes' pattern at the line of a poem or song (often in nursery rhymes). Can you recall some nursery rhymes? Letters are used to indicate the lines that rhyme.

Rhyme Scheme

May be considered as a pattern concerning words. It is a Japanese poem, typically about nature, with 17 syllables divided into three lines of 5, 7, and 5 syllables.

Haiku

A list of numbers that follow a particular sequence or order.

Number Patterns

Where the difference between two consecutive terms is called the common difference.

Arithmetic Sequence

Sequence where a term is multiplied by a constant, called the common ratio, to get the next term.

Geometric Sequence

The terms of this is related to the number of dots needed to create a triangle. Begin forming a triangle with three dots; one on top and two on the bottom. The next row would have three dots, making a total of six dots. The next row in the triangle would have four dots, making a total of 10 dots. The following row would have five dots, for a total of 15 dots. Therefore, a triangular sequence begins: "1, 3, 6, 10, 15…"

Triangular Numbers

The terms are the squares of their position in the sequence. A square sequence would begin with "1, 4, 9, 16, 25…"

Square Numbers

The terms are the cubes of their position in the sequence. Therefore, a cube sequence starts with "1, 8, 27, 64, 125…"

Cube Numbers

He was born in Pisa, Italy, in 1170. He was recognized and well known for popularizing the Hindu-Arabic numeral system or decimal system in Europe. He advocated the use of the digits 0 to 9 and of the place values.

He is popularly known as Fibonacci, a shortened word for the Latin term "fillius Bonacci," which means "son of Bonacci" because his father was Guglielmo Bonaccio. He discovered the famous FIBONACCI SEQUENCE. Fibonacci was able to find this number sequence while looking at how generations of rabbits breed.

Leonardo Pisano / Leonardo of Pisa

The breeding of these animals led to Leonardo’s discovery of the numbers in the Fibonacci sequence.

Rabbits

Fibonacci Numbers in Nature - In the number of petals of flowers

Fibonacci Numbers in Nature - In the number of sections in fruits

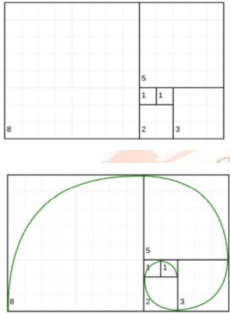
Using the first ten (10) numbers in the Fibonacci sequence 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 as dimensions of adjacent squares, you can create a Fibonacci spiral. When arranged in a certain way, the Fibonacci sequence creates a special spiral pattern.

The Fibonacci Spiral

Can be found in a nautilus shell, photographs of storms, arrangement of sunflower seeds, skins of pineapples and pinecones, and specific body parts.

The Fibonacci Spiral

The symbol for it is the Greek letter "phi" – Ф (uppercase letter) or φ (lowercase letter).

It is named after the Greek sculptor Phidias.

It is an irrational number equal to 1.61803398874989484820... (approximately equal to 1.618). It is also equal to \varphi=\frac{\sqrt5+1}{2} and φ = 2 (Sin 54°)

It is also known as Divine Ratio or Divine Proportion.

The Golden Ratio

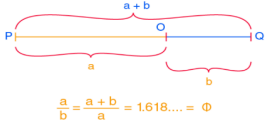
Using a line segment, divide it into two parts in such a way that the ratio of the longer part to the shorter part is equal to the ratio of the whole segment to the longer part.

The Golden Ratio in the Fibonacci Sequence

The Fibonacci spiral, as mentioned in the previous lesson, is constructed using the numbers in the Fibonacci sequence. The Fibonacci spiral is also known as this.

Many artists who lived after Phidias have used the Golden Rectangle and the Golden Ratio like Leonardo Da Vinci in his painting "Mona Lisa."

The Golden Spiral

Rectangle whose sides are in the proportion of the Golden Ratio. This may be observed in notable architectural structures dating back to ancient times as well as art.

Temples like the Parthenon in Greece are believed to have the Golden Ratio in them.

The Golden Rectangle

The face, follows the Divine Proportion. The closer the body parts' proportion is to the Golden Ratio, the more aesthetic and beautiful the body is.

Proportions of the Human Body

Mathematics uses these instead of words.

Symbols

Letters for variables (like x or y) or counting values (like m or n).

Lowercase

Letters for sets (like X or Y) and formulas.

Uppercase

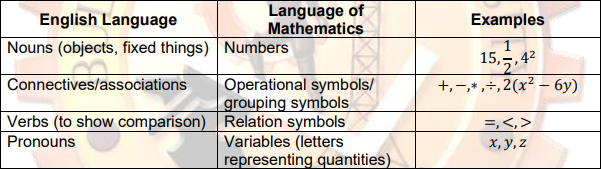
The English Language and the Language of Mathematics

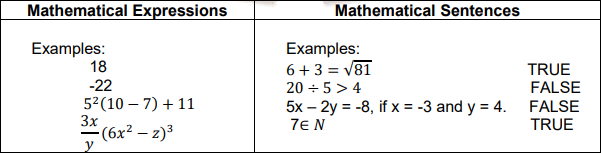
Expression vs. Sentence in the Language of Mathematics

Knowing how to translate English expressions to mathematical expressions is essential in problem-solving. The first step in any problem-solving situation in mathematics is always to read and understand the problem. Translating the words into mathematical symbols is next.

Translating English Expressions to Mathematical Expressions

Representation of the statement "The sum of two numbers is 12."

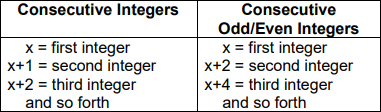
Representation of Consecutive Integers

The following phrases simply mean the subtraction of the past number of years from the present age: years ago, years back, was at that time, during or in the last _ years.

The following phrases mean the addition of the future number of years to the present age: years from now, years hence, years after or in _ more years.

Representation of Ages

Let h = first digit or hundreds digit, t = second digit or tens digit, and u = third digit or unit digit.

Representation of Two-digit and a Three-digit Number

Powerful building block of mathematics when applied to different situations. Some of the higher mathematics disciplines whose common denominator is set are the following: Graph Theory, Abstract Algebra, Real Analysis, Complex Analysis, Linear Algebra, and Number Theory.

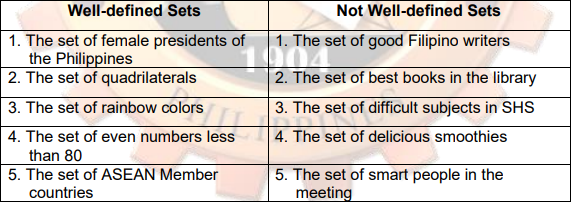
Sets

Counting numbers (also called positive integers).

• 1, 2, 3,…

(N) Natural Numbers

Naturals numbers, their negatives and 0.

• …, -4, -3, -2, -1, 0, 1, 2, 3, 4,…

(Z) Integers

Numbers that can be represented as a/b, where a and b are integers and b≠0. The decimal representations are terminating or repeating.

• -15, -2, 0, 23, -1/4, 3/7, 15/2, -2.75, 1.625, -0.333…, 5.272727…

(Q) Rational Numbers

Numbers that cannot be expressed as the ratio of two integers. They are the nonrepeating and non-terminating decimals.

• √2 = 1.414213562 … , 𝜋 = 3.141592654 …

(Q’) Irrational Numbers

Rational and Irrational.

(R) Real Numbers