3- Rational consumer choice

Draw a budget constraint

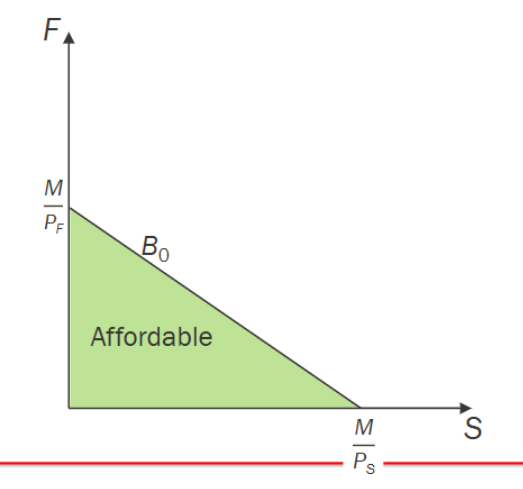
Where is the best affordable bundle

On the budget constraint so prices add up to M

Marginal benefit and cost are equal

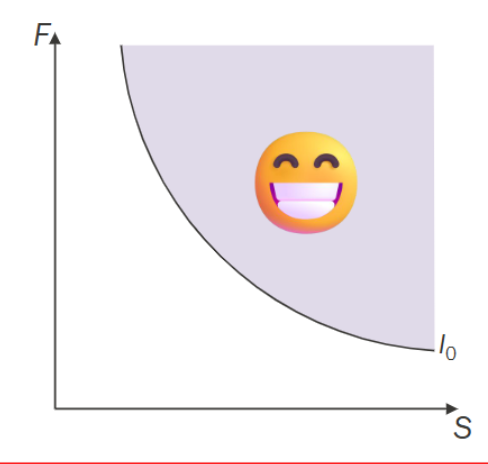
Draw an indifference curve

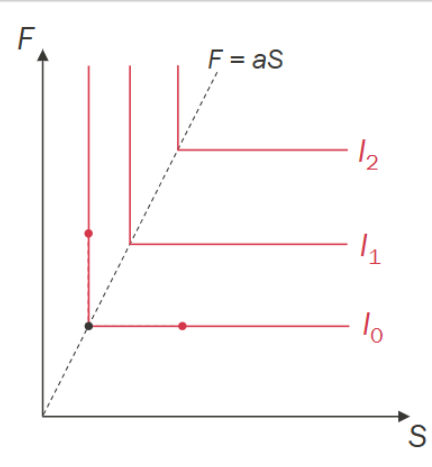
What will the indifference curve look like if shelter and food is consumed in fixed proportions

They are perfect complements

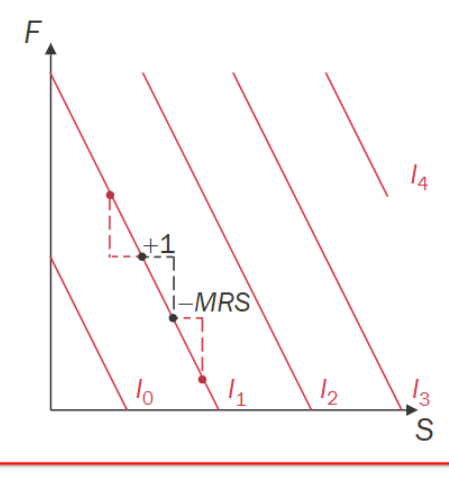
What does the indifference curve look like if the consumer is willing to give up the same amount of food for a unit of shelter always

Perfect substitutes

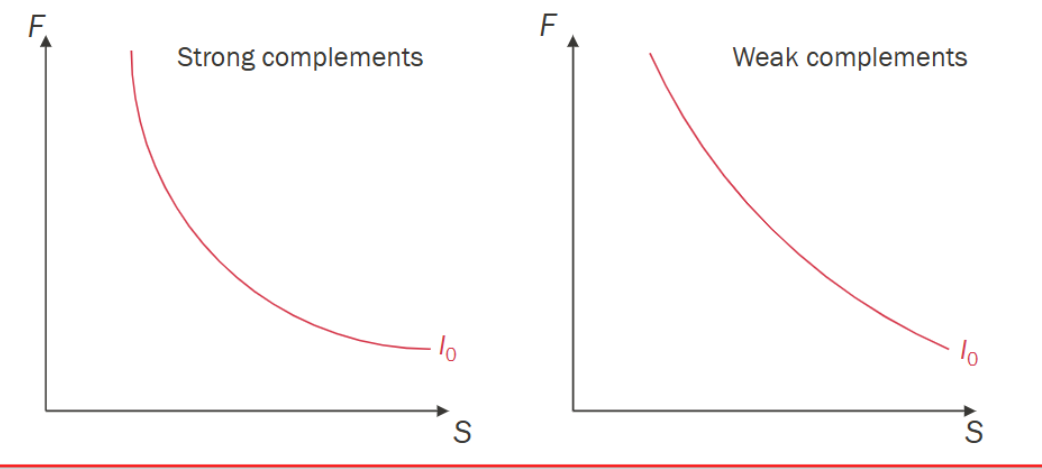
What does a strong and a weak complement look like on an indifference curve

What is the equation for the optimal bundle

What is a consumption bundle

A combination of two or more goods

If the consumer is on the budget constraint what does this say about their income

That all of their income is being spent

What is the equation for a budget constraint

take form y = bx + a - convert it into the graph form

Constructing indifference curves

Find intersections with points using logic about bundles ect

Consumer is indifferent to all bundles on the indifference curve

How to choose which bundle is ideal on indifference curve

Consumers prefer a variety of goods not lots of the same so often in the middle

What is MRS

Marginal rate of substitution

Effectively the average gradient of a slope in a certain period for example 1 more of Y cause - change in X and so we use this formula

-change in x / 1 (Change in y)

The maximum amount of a good the consumer is willing to give up for one more unit of another good

What can be said if the best affordable bundle meets the indifference curve`

MRS = Px / Py

Slope of indifferent curve = slope of budget constraint

Formula of change in total utility

Derivative of - change in utility = Marginal utility of change in F + Marginal utility of change in X

What is MRS formula when change in F and change in Y get smaller

MRS = marginal utility s / marginal utility f

So marginal utility s / marginal utility f = ?

Ps / Pf

GO OVER LAGRANGIAN MULTIPLIER + ORDER CONDITIONS

At end of week 3 intro video