Biostatistics exam 3 - Linear Regression

Regression

regression is a method that predicts values of one numerical variable from values of another numerical variable

• Fits a line through the data

- used for prediction

- measures how steeply one variable changes with another

Correlation versus regression

• correlation measures the aspects of the linear relationship between two numerical variables

- measures the association between X and Y

• regression predicts values of Y given X

Linear regression

• the most common type of regression ( there are nonlinear models)

• draws a straight line through the data to predict the response variable (Y) from the explanatory variable (X)

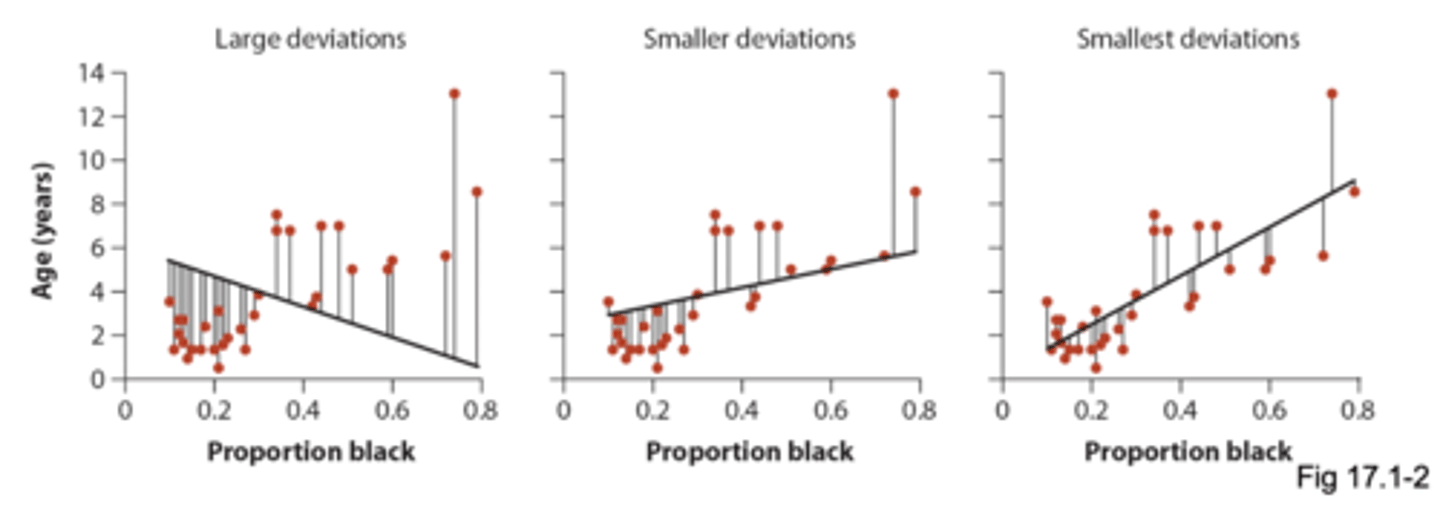
least squares regression

Line for which the sum of all the squared deviations in y is smallest

• deviations: distance between data point and the line

Formula for the linear regression

• a = y-intercept, b is the slope

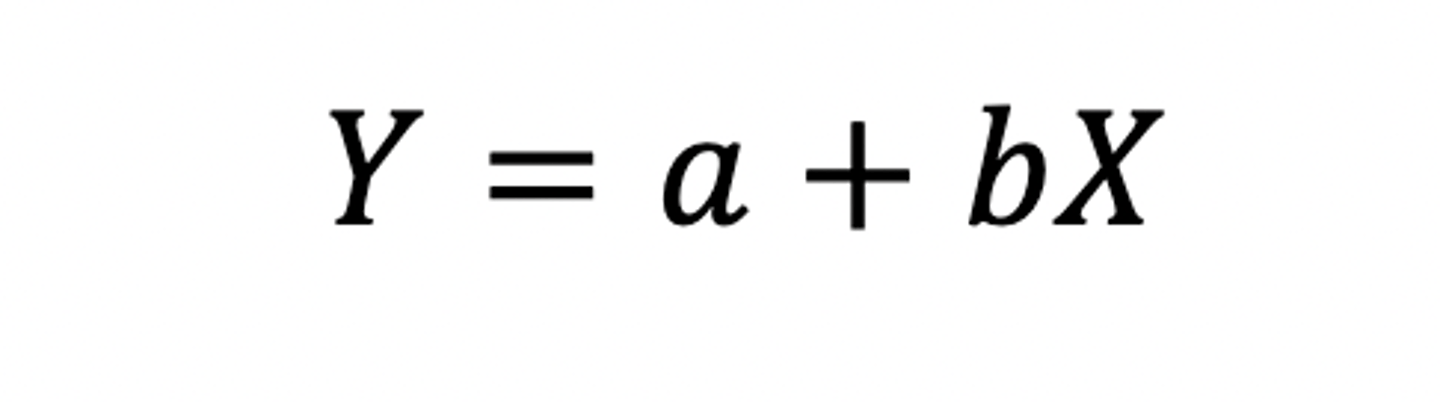
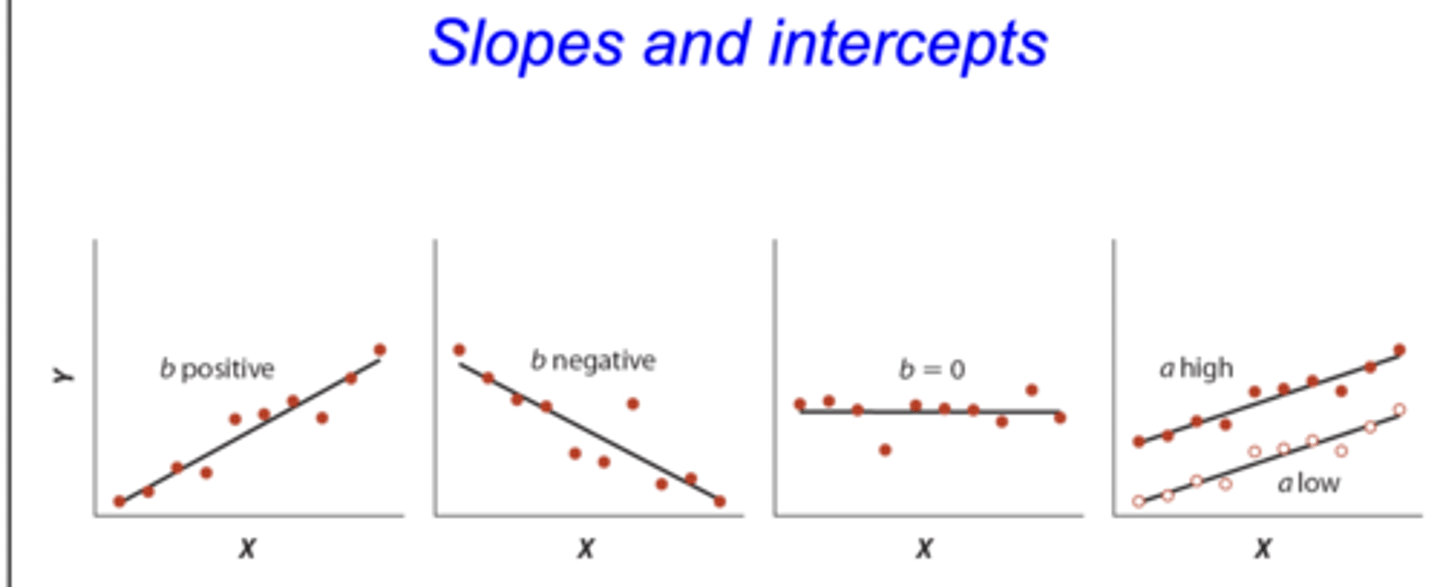
Slope of a linear regression

• the slope of a linear regression is the rate of change in y per unit X (rise of a run)

• also measures direction of prediction

- positive: as X increases y increases

- negative: as X increases y decreases

How to calculate the slope (linear regression) - equation

• numerator measures how deviations and X and Y vary together (can be pos or neg)

• denominator is the sum of squares for x

How to calculate the intercept (linear regression)

• one slope is calculated, getting intercept is straightforward because the least squares regression always goes through (Xbar, Ybar)

• plug mean values into line formula → rearrange to solve for intercept

estimates / statistics and parameters for a linear regression

• estimates/statistics: (b) slope and intercept (a)

- estimated from a sample of measurements

• Parameters: slope (β) and intercept (α)

- from the true population

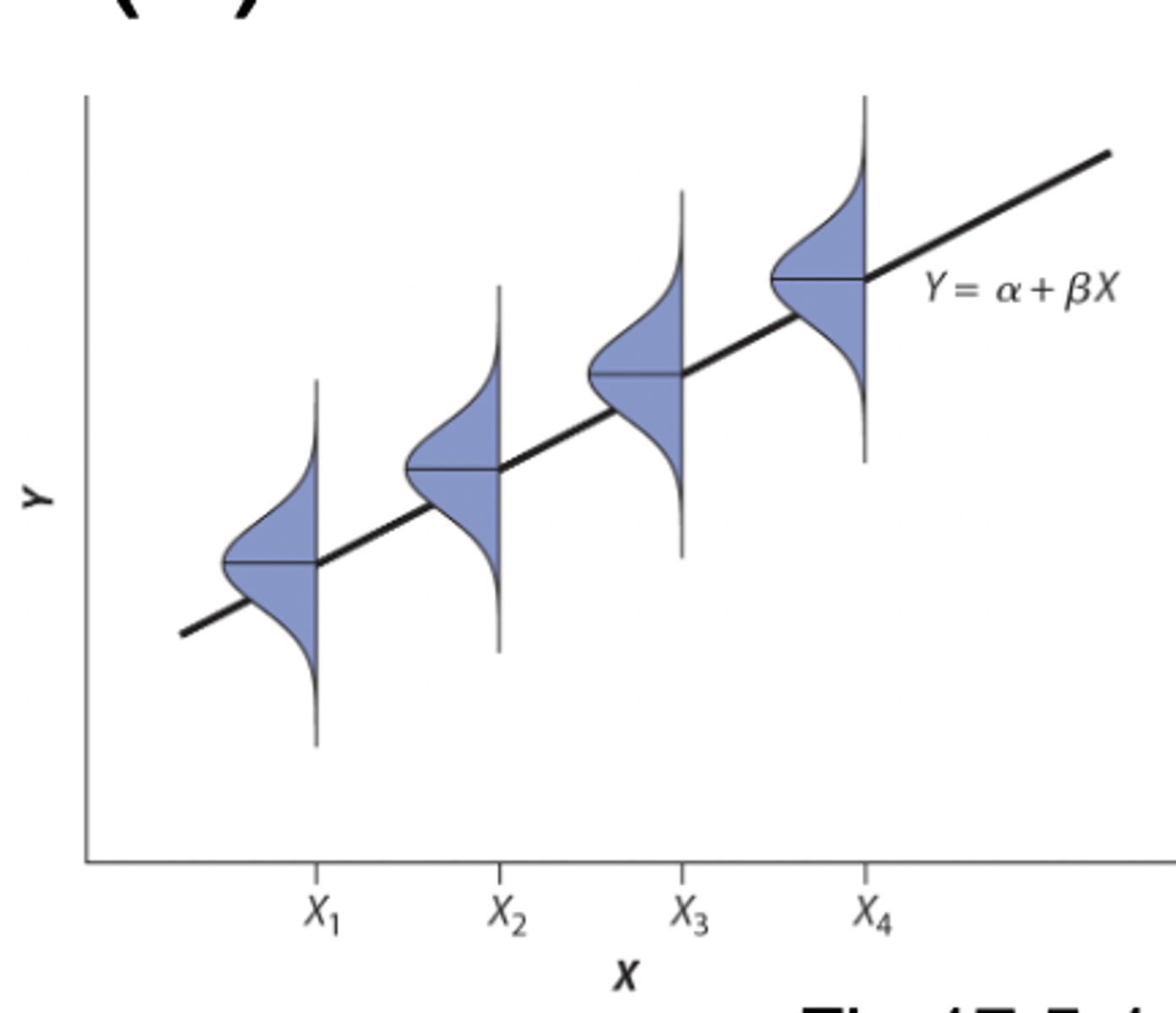
regression assumption

Regression assumes that there is a population for every value of X, and the mean Y for each of these populations lies on the regression line

• assumes the spread is the same in each subpopulation (you don't want a funnel)

Predicting values with a linear regression

•can predict values of Y for any specified value of x

- you can't predict X based off Y because (in the study) you're using the explanatory variable to predict Y not the other way around

• predictions are mean Y for all individuals with value X

• designated Y^ "Y-hat"

• use the linear regression formula to plug in a value of x and solve for y

Residual

the residual of a point is the difference between its measured Y value and the value of y predicted by the regression line

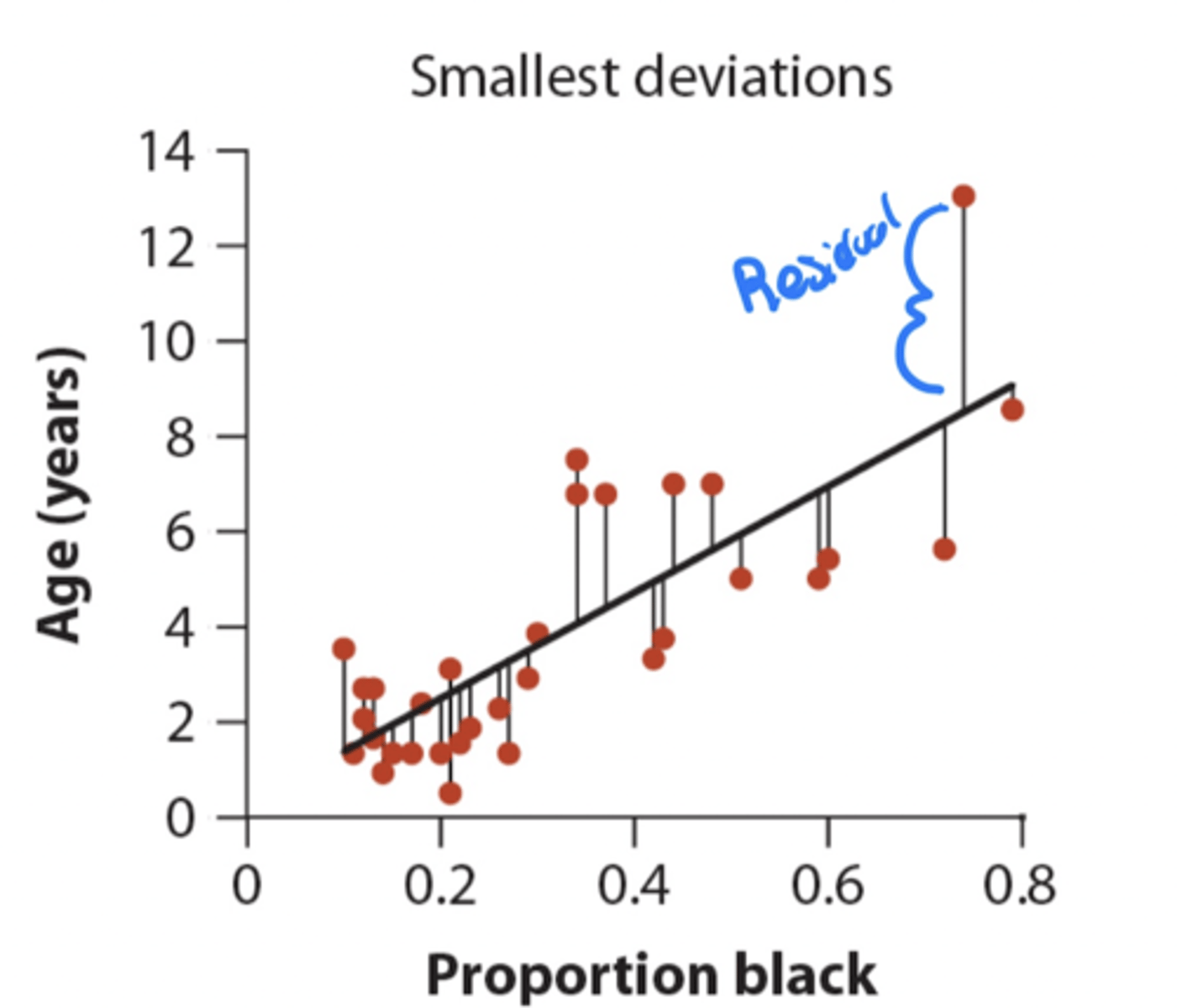
How do you measure how well the data fits the line?

• residuals measure the scatter of points above and below the least squares regression line

- can be positive or negative

• variance in residuals (MSresidual) quantifies the spread of the scatter

- residual mean square

- analogous to error square in ANOVA

- used to quantify the uncertainty of the slope

Residual mean square equation

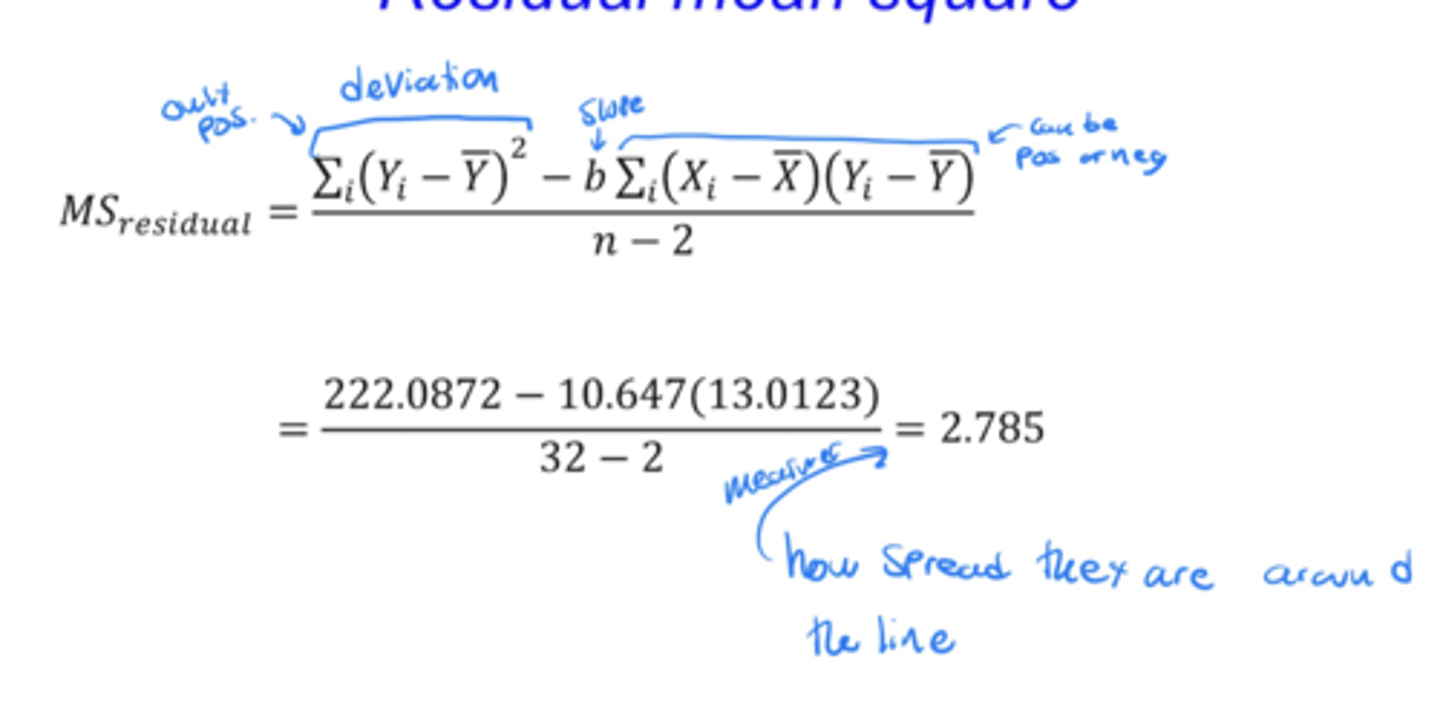
standard error of the slope (equation)

• uncertainty (precision) with the sample estimate (b) of the population slope (β)

• the sum of squares in the denominator takes into account as you add more data points you expect more spread

• in the numerator is the spread of the residuals

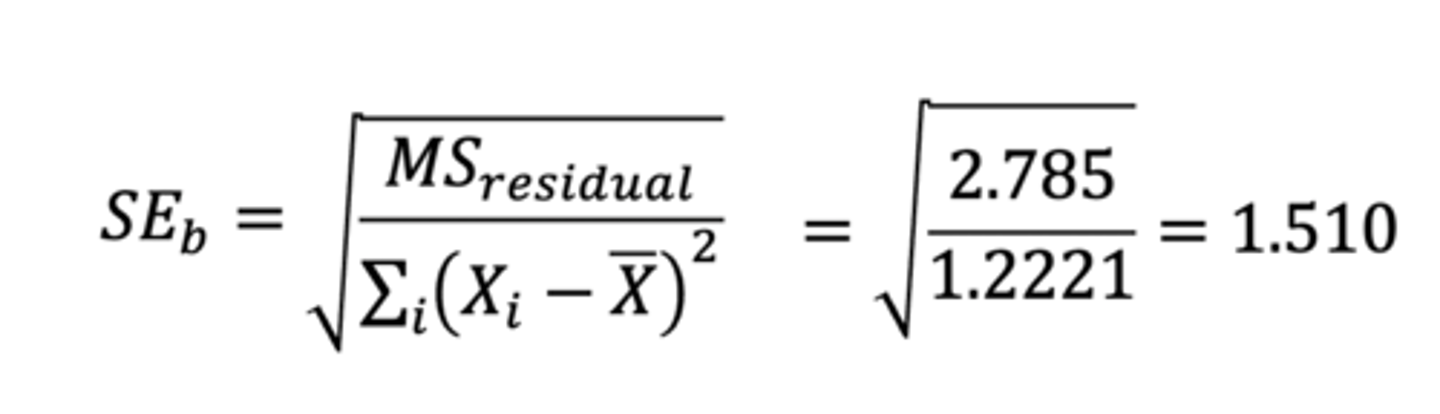
Confidence interval of the slope

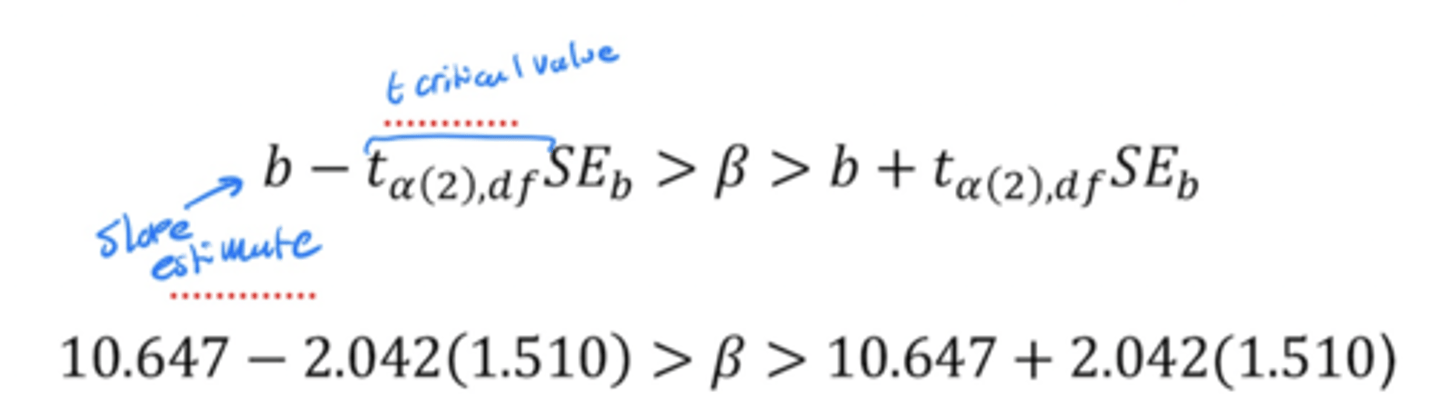
The two types of predictions

1. predict mean Y for a given X

- e.g. what is the mean age of all male lions whose noses are 60% black

2. predict single Y for a given X

- e.g.how old is that lion over there with a 60% black nose

* both predictions give the same value of Y-hat but they differ in precision

• can predict mean with more certainty than a single value

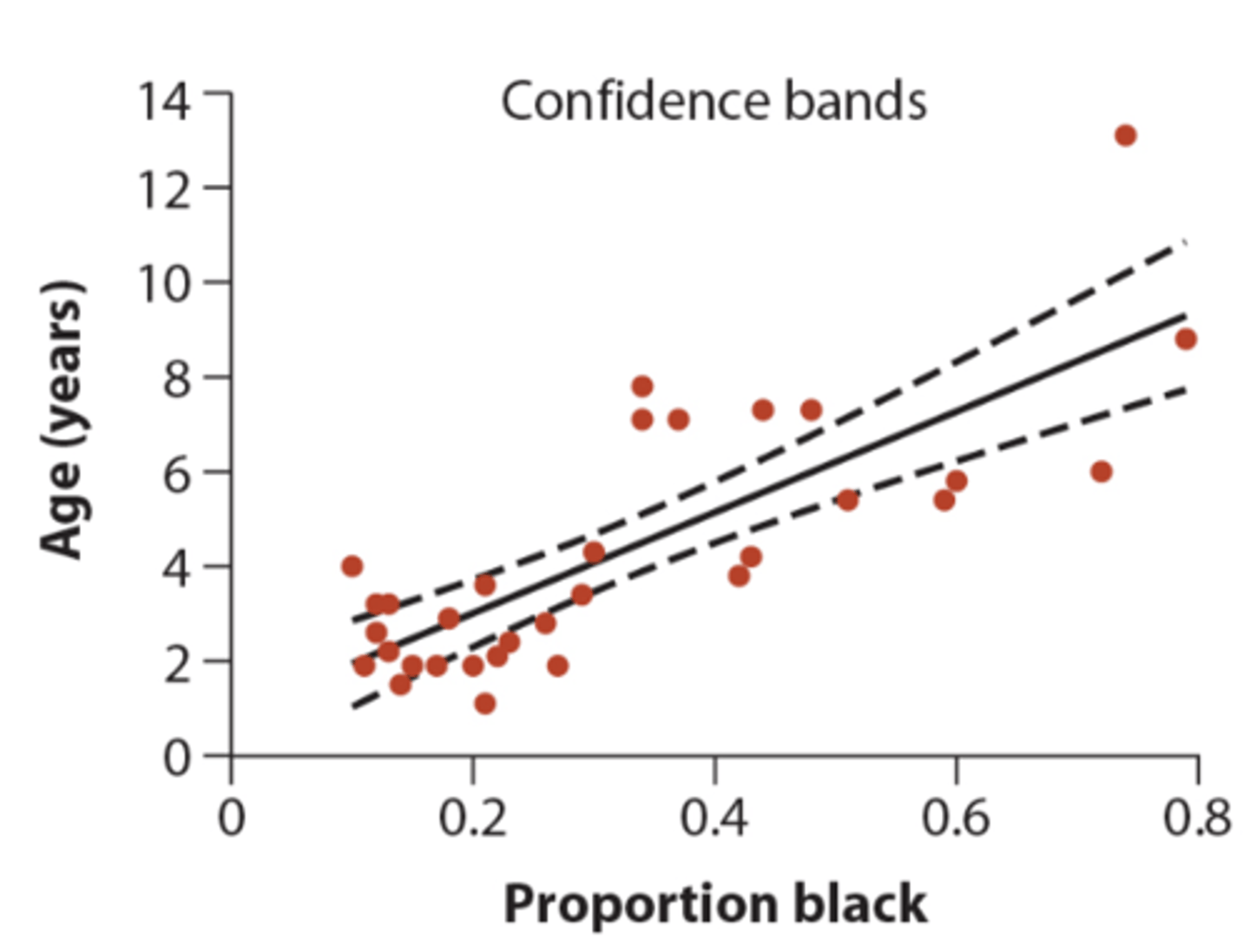
Confidence bands

measure the precision of the predicted mean Y for each given value of X

• curved because when sample size is smaller it gets wider

• width will be skinniest at the means of X-hat and Y-hat

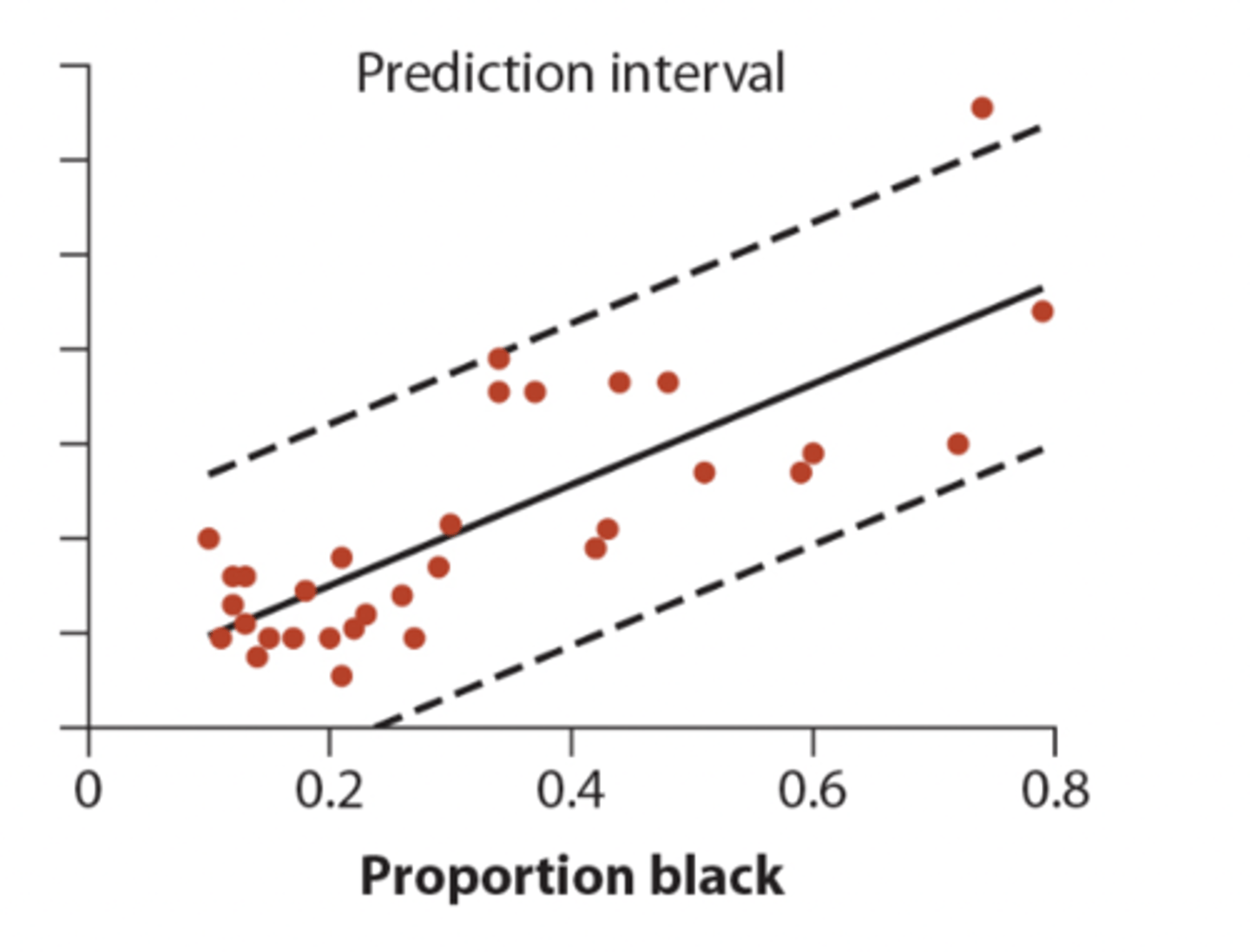
Prediction intervals

Measure the precision of the predicted single Y values for each X

• wider than confidence bands because predicting a single Y value is less precise than predicting a mean Y

Interpolation

Regression should be used to predict Y for any value of X lying between the smallest and largest values of X

Extrapolation

The prediction of the value of a response variable (Y) outside the range of X values in the data

• extended prediction Beyond where you sampled

• not recommended because there's no way to ensure the relationship continues to be linear beyond the range of the data

Hypotheses for testing a slope

H₀: β = 0

Ha: β ≠ 0

test statistic for regression slope

t-statistic → measures how well our data fit the expectation of our data

t-statistic equation for regression slope

• SEb = measures uncertainty

• β₀ = Null

• df = n-2

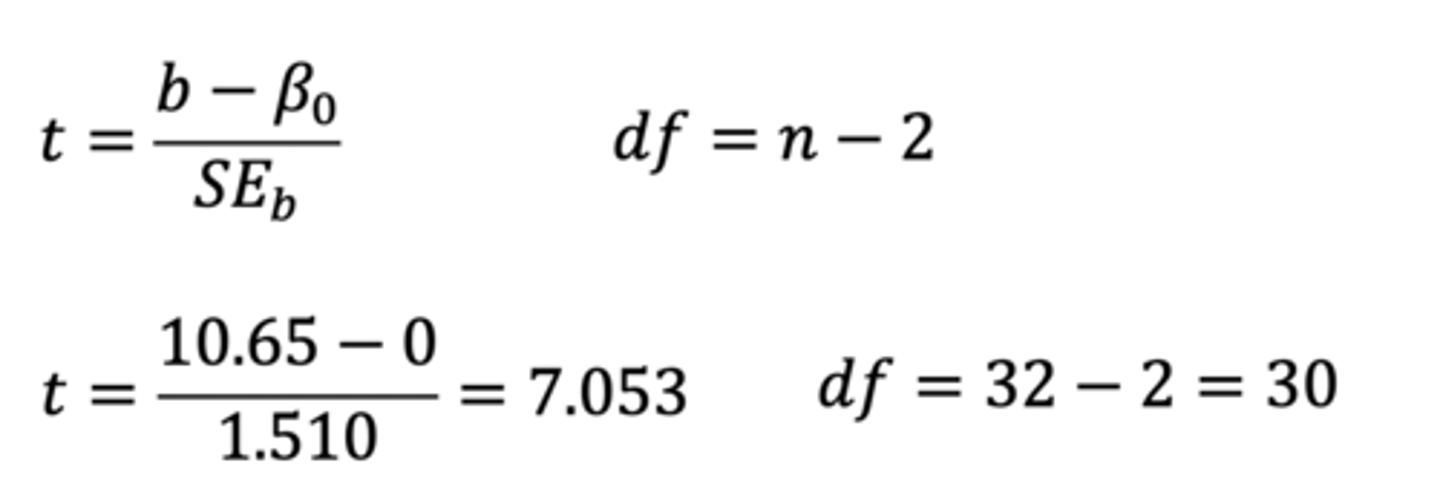
how to get a p-value from the test statistic

determine the critical value for the t-distribution and calculate p using a stats table or computer

ANOVA (F) approach

In regression framework:

• deviations between the predicted values of Yi-hat and Ybar

-analogous to MSgroups

• deviations between each Yi and it's predictive value Yi-hat (residuals)

- analogous to MSerror

• using ANOVA approach will generate the same p-value as the t-test approach

• can be used to measure R²: the fraction of the variation in Y that is "explained" by X

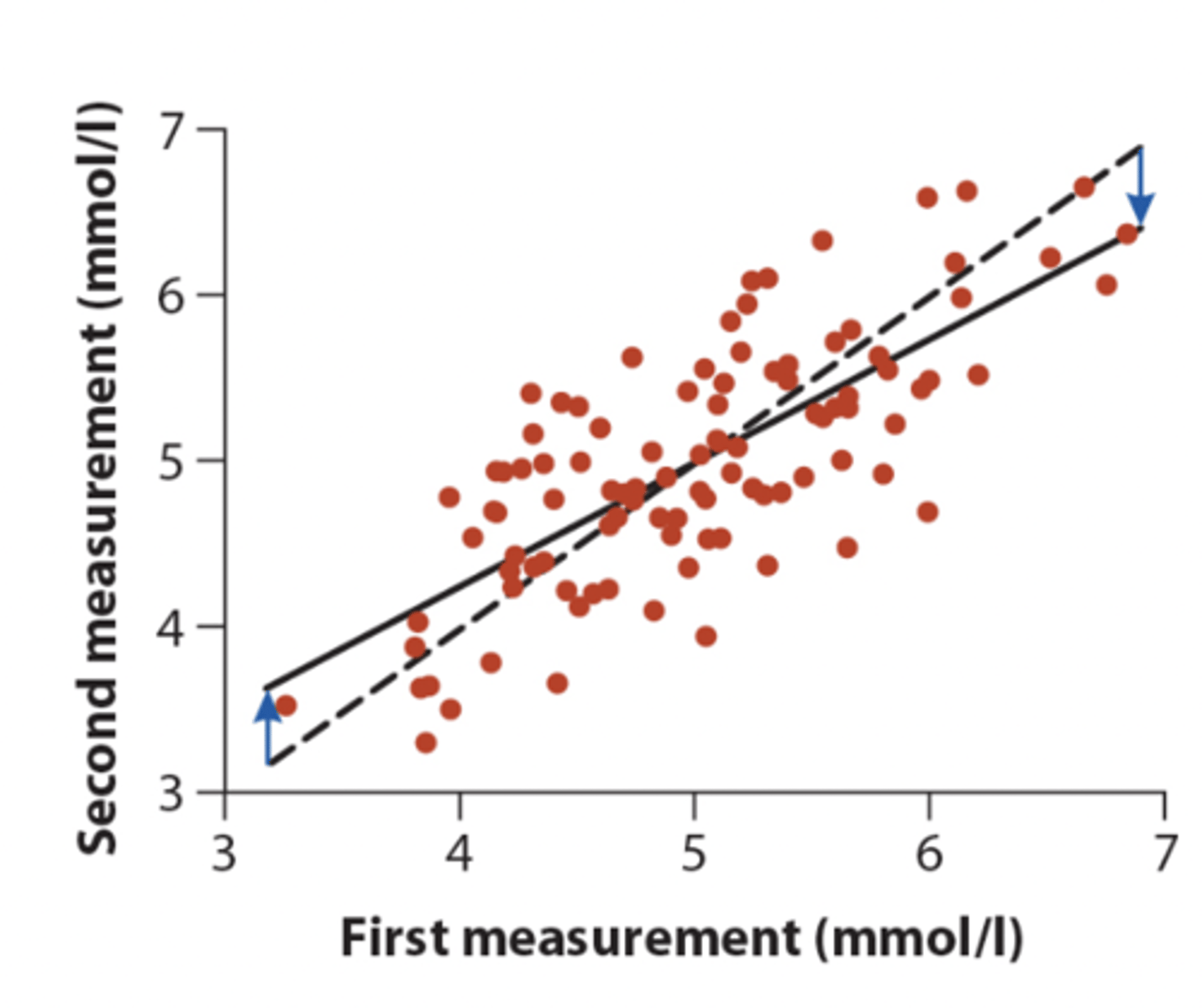
Regression toward the mean

Results when two variables measured on a sample of individuals have a correlation less than one. Individuals that are far from the mean for one of the measurements will, on average, like closer to the mean for the other measurement

• in pic: solid line = linear regression, dashed line = one-to-one line with slope of 1

• are people regressing to mean or is the drug working

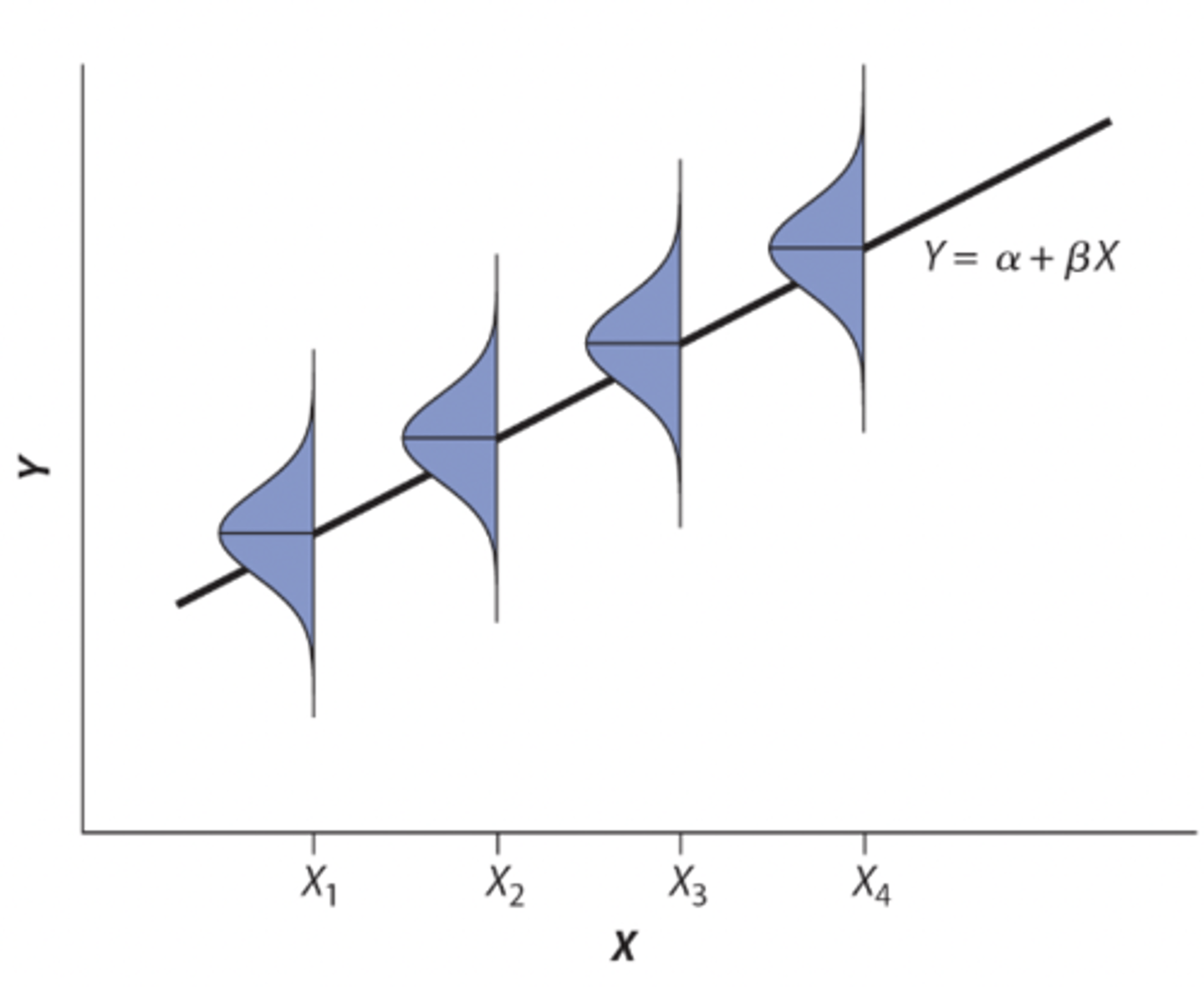
Assumptions of linear regression

At each value of X:

• there is a population of Y-values whose mean lies on the regression line

• the distribution of possible Y-values is normal (with the same variance)

• The variance of Y-values is the same at all values of X

• the Y measurements represent a random sample from the possible Y-values

3 possible issues when trying to do a linear regression

1. outliers

2. nonlinearity

3. non-normal and unequal variants

How to deal with outliers

If only one (or a low number) then it may be reasonable to report regression with and without outlier

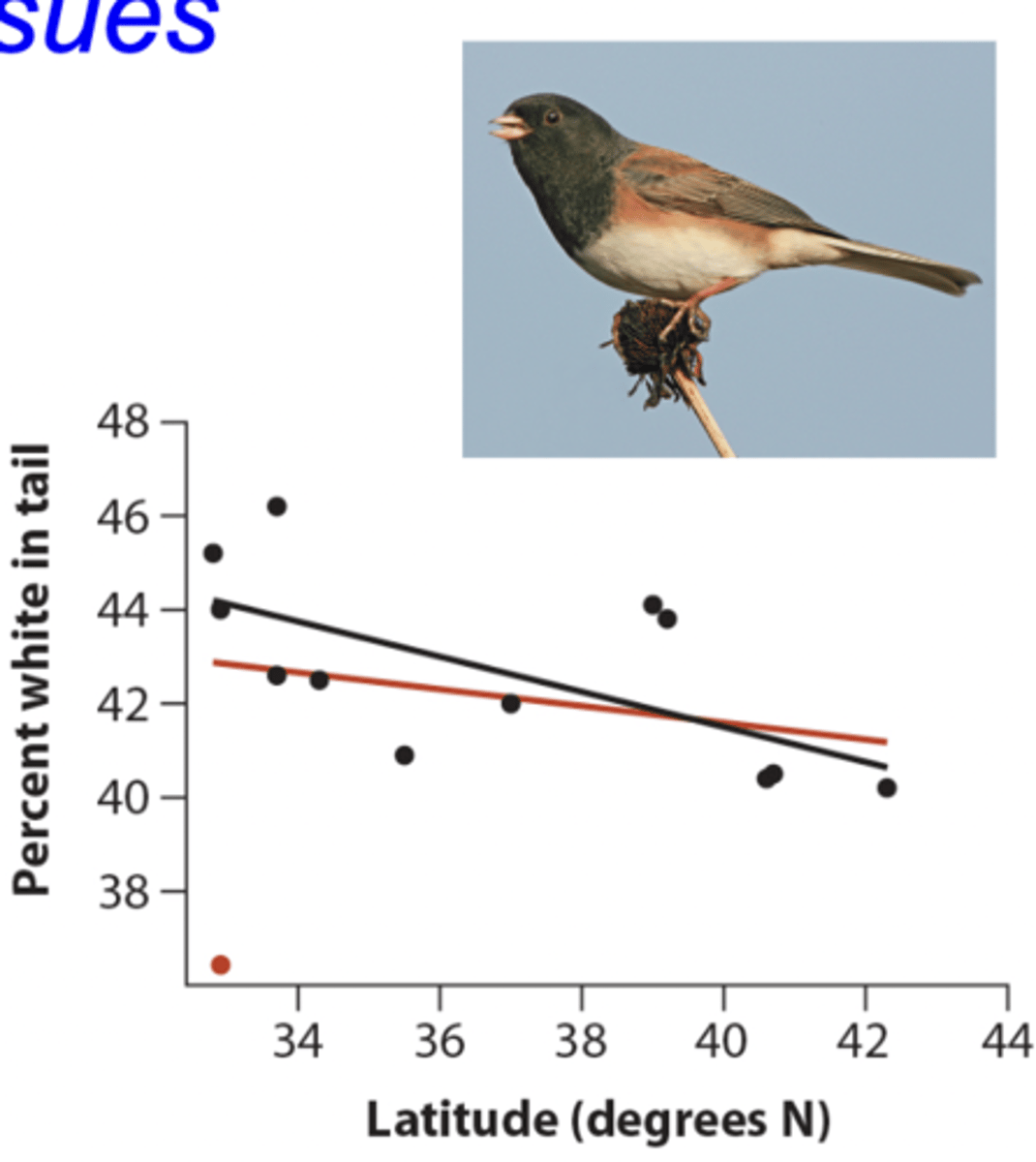
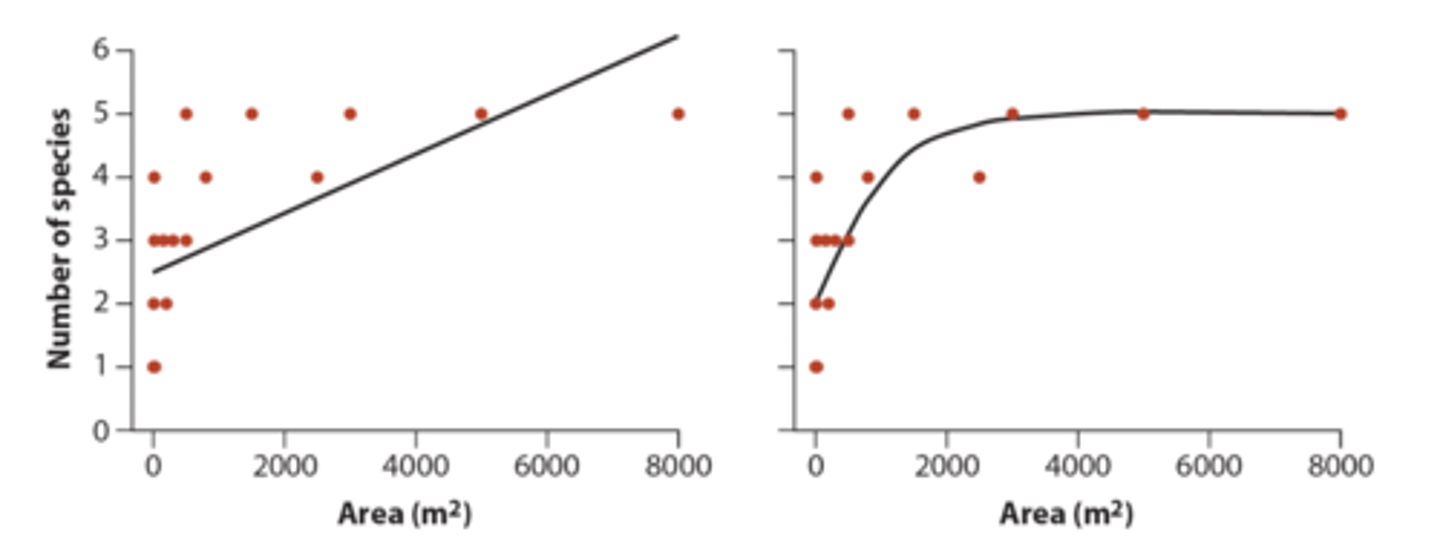
How to detect nonlinearity

Can be detected by inspecting graphs

How to detect non-normality and unequal variances

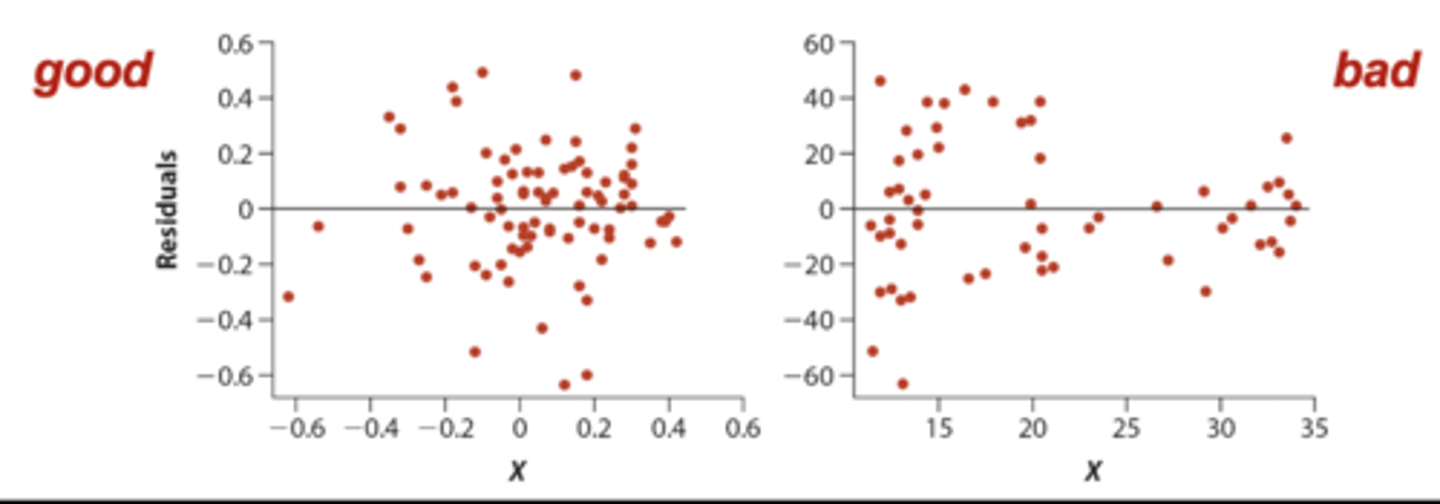
Residual plot

Residual plot

Residual of every data point (Yi - Yi-hat) is plotted against Xi

• if assumptions of normality and equal variances are met then there should be a roughly symmetric cloud above / below line at zero

- you don't want a funnel (violation of subpopulation distribution assumption)