Calculus 1 Final Exam Study Guide

The (Limit) Definition of the Derivative F'(X)

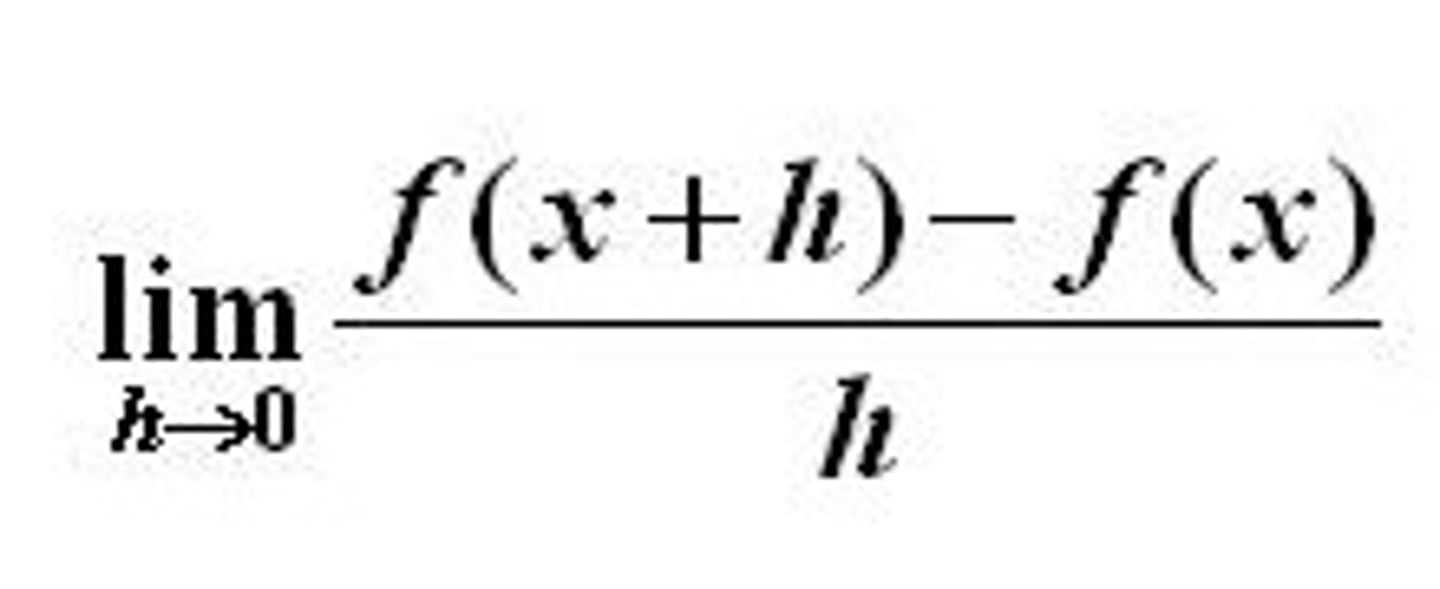
Mean Value Theorem

Suppose y=f(x) is continuous over a closed interval [a,b] and differentiable on the interior (a,b) then there is at least 1 point "c" such that

The Definition of Continuity at x=a

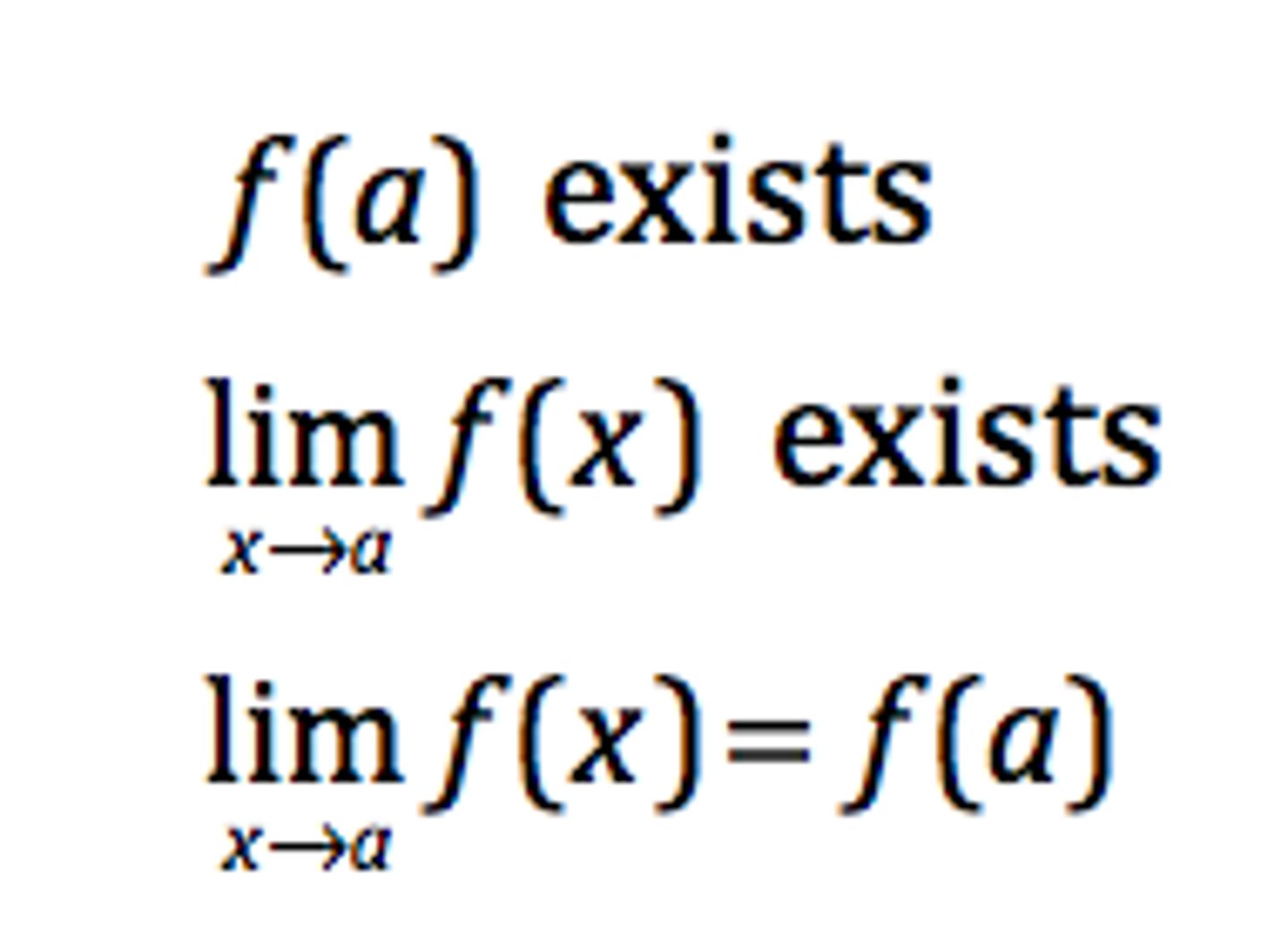
First Fundamental Theorem of Calculus

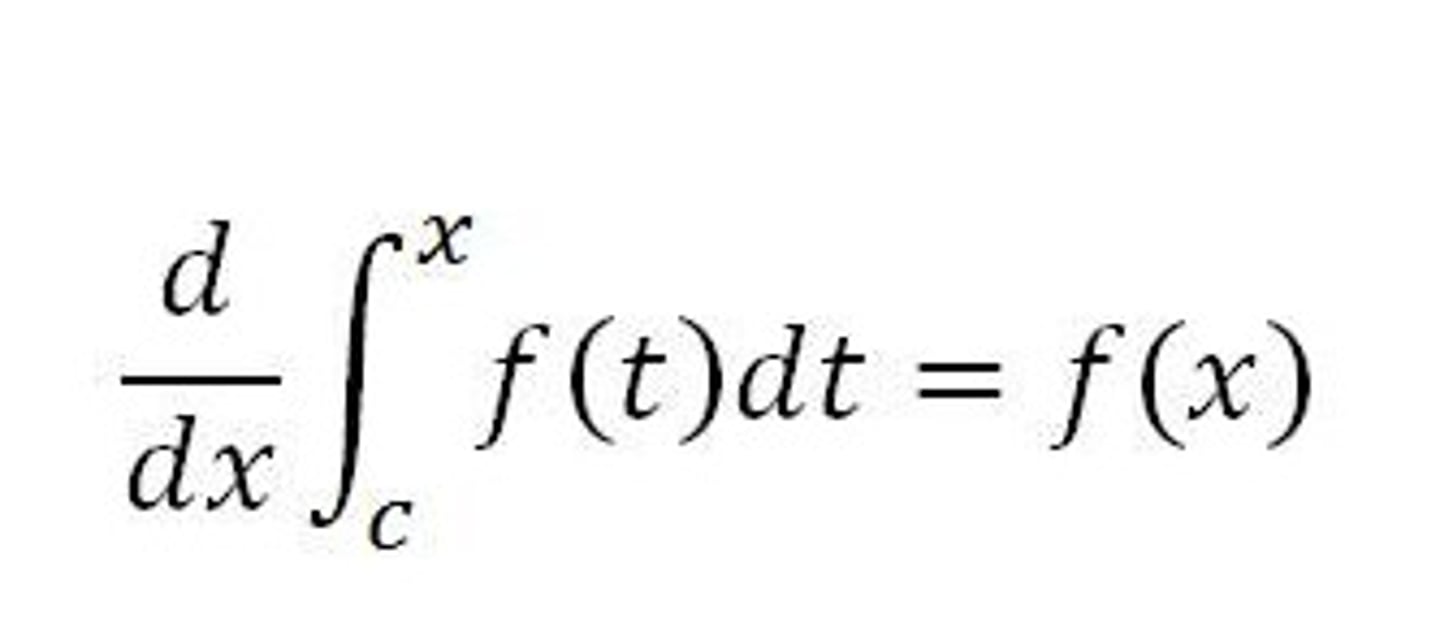
Second Fundamental Theorem of Calculus

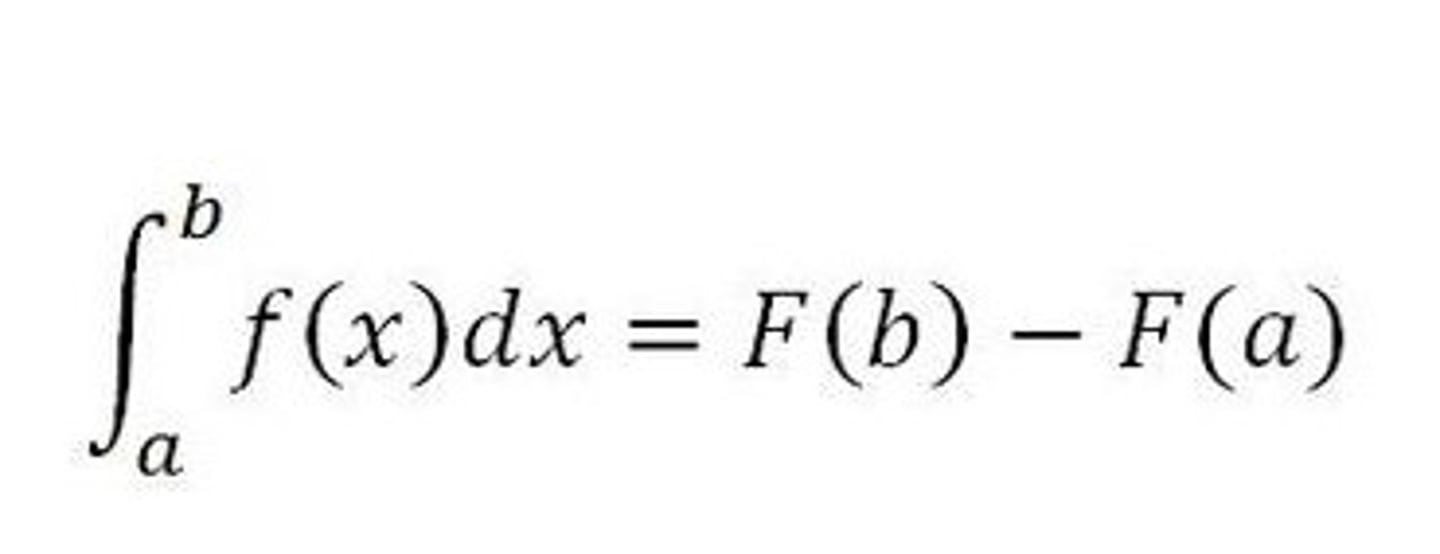
The Extreme Value Theorem

If f is a continuous function on a closed interval [a,b], then f attains an absolute max M and absolute min m on the interval [a,b] that is there exists x1, x2 in [a,b] such that f(x1)=M and f(x2)=m.

Average Rate of Change

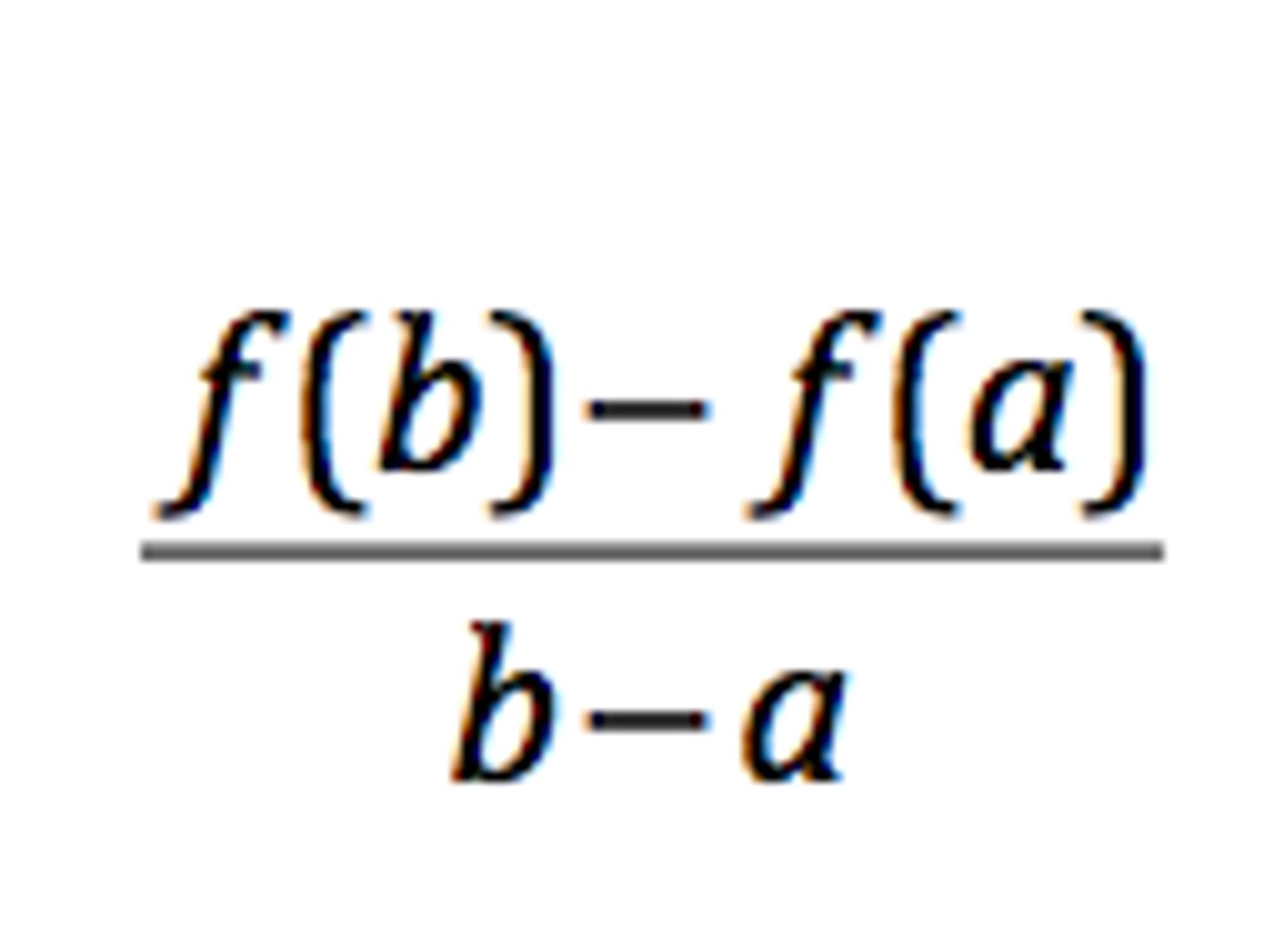
Average Velocity

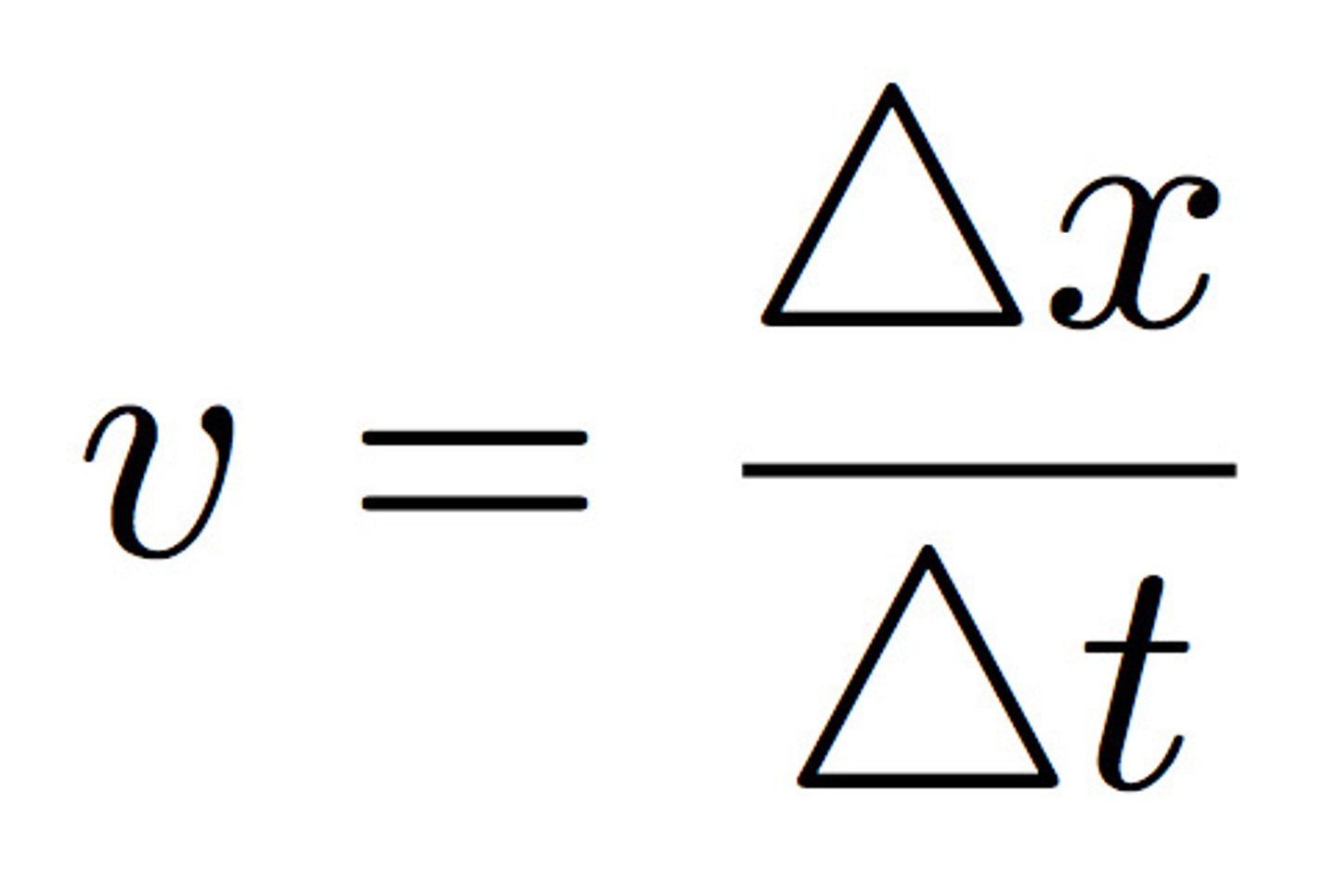
Instantaneous Rate of Change

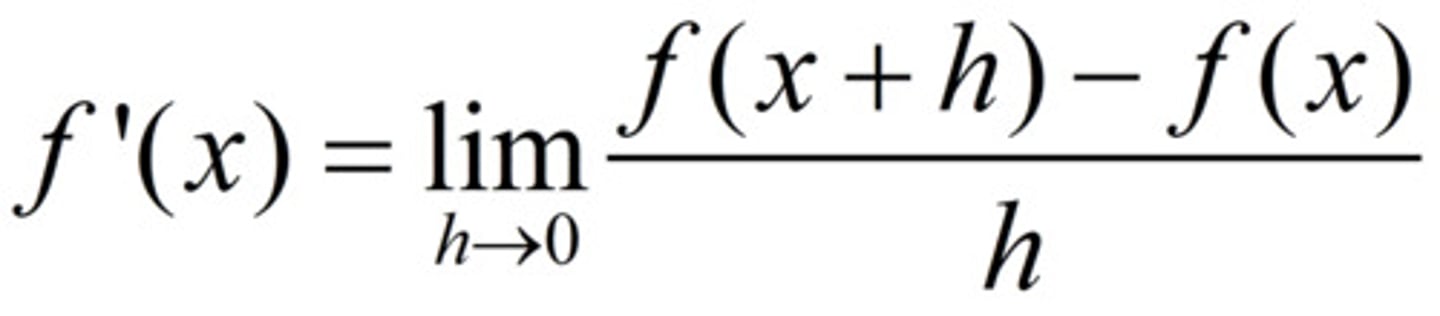
Average Value of a Function

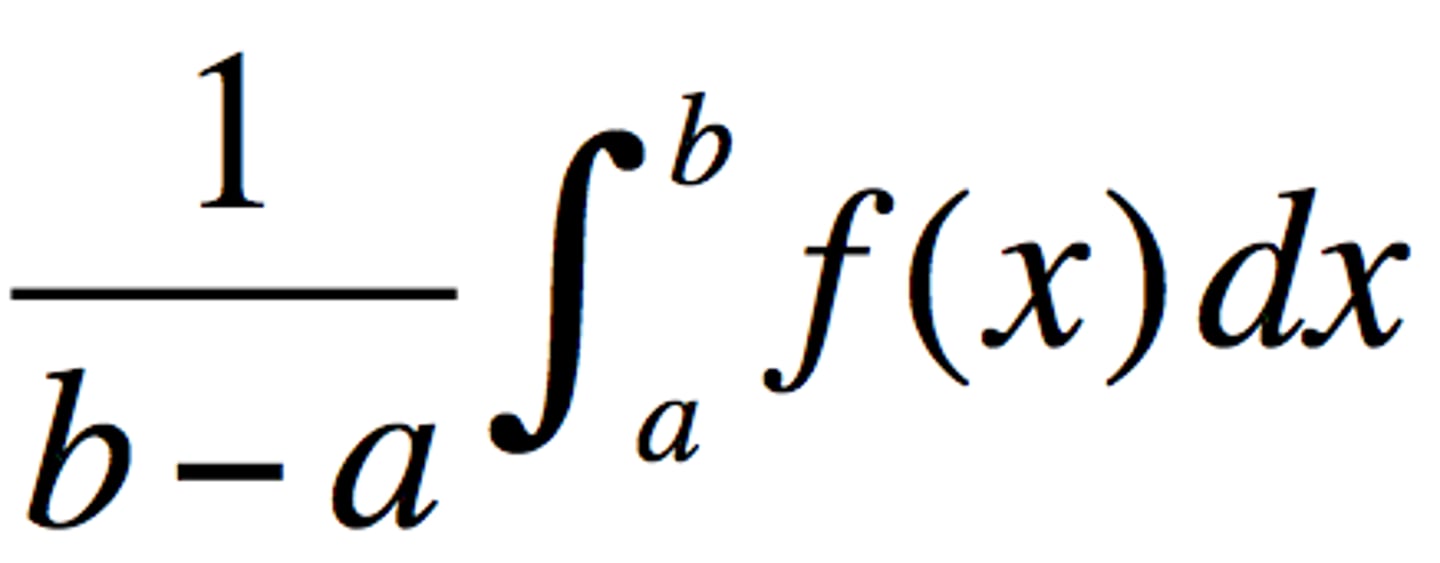
Tangent Lines

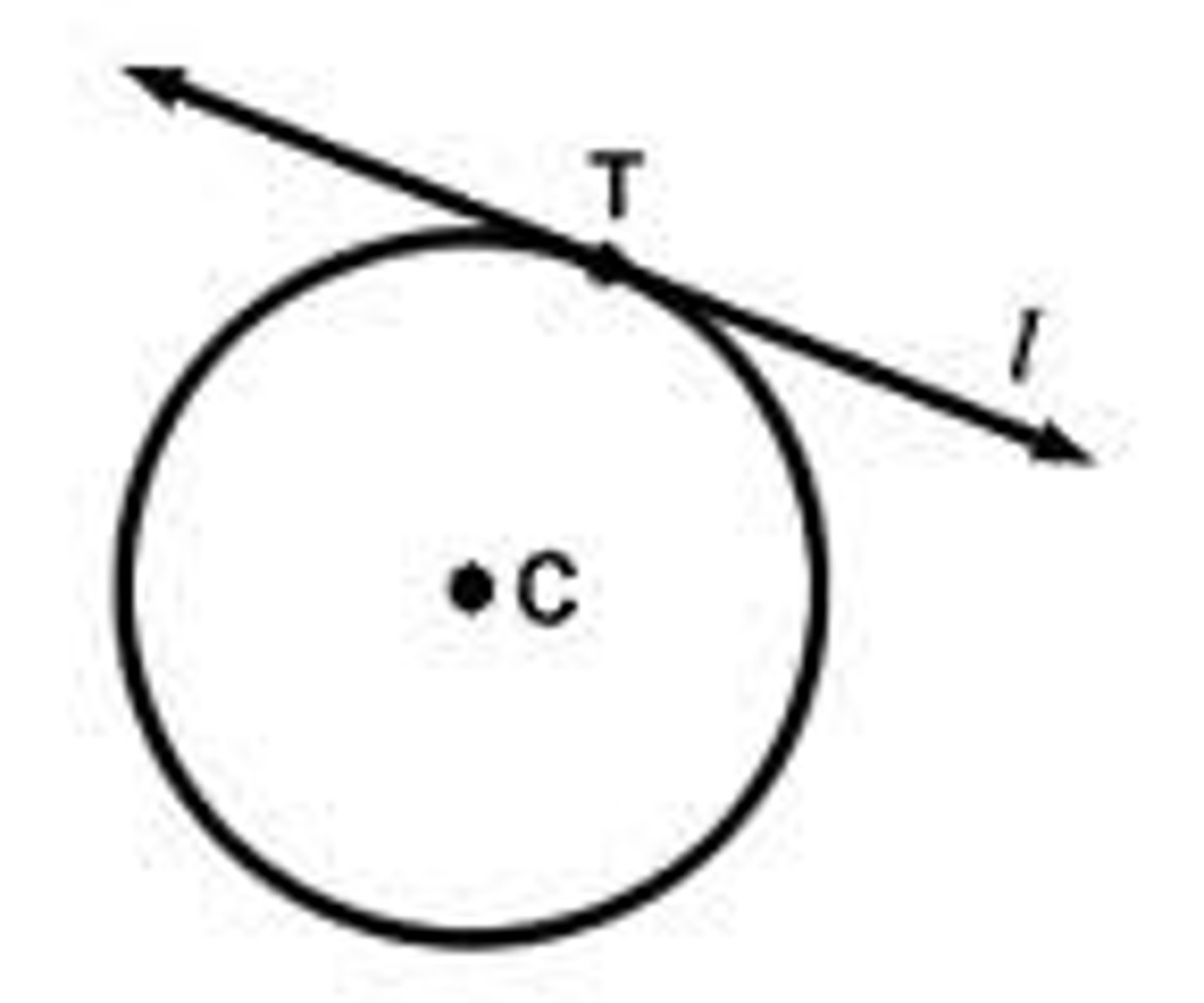
Linearization of a Function at a point

Tangent line- if f is differentiable at x=a; L(x)=f(a)+f'(x-a)

Surface Area of Sphere

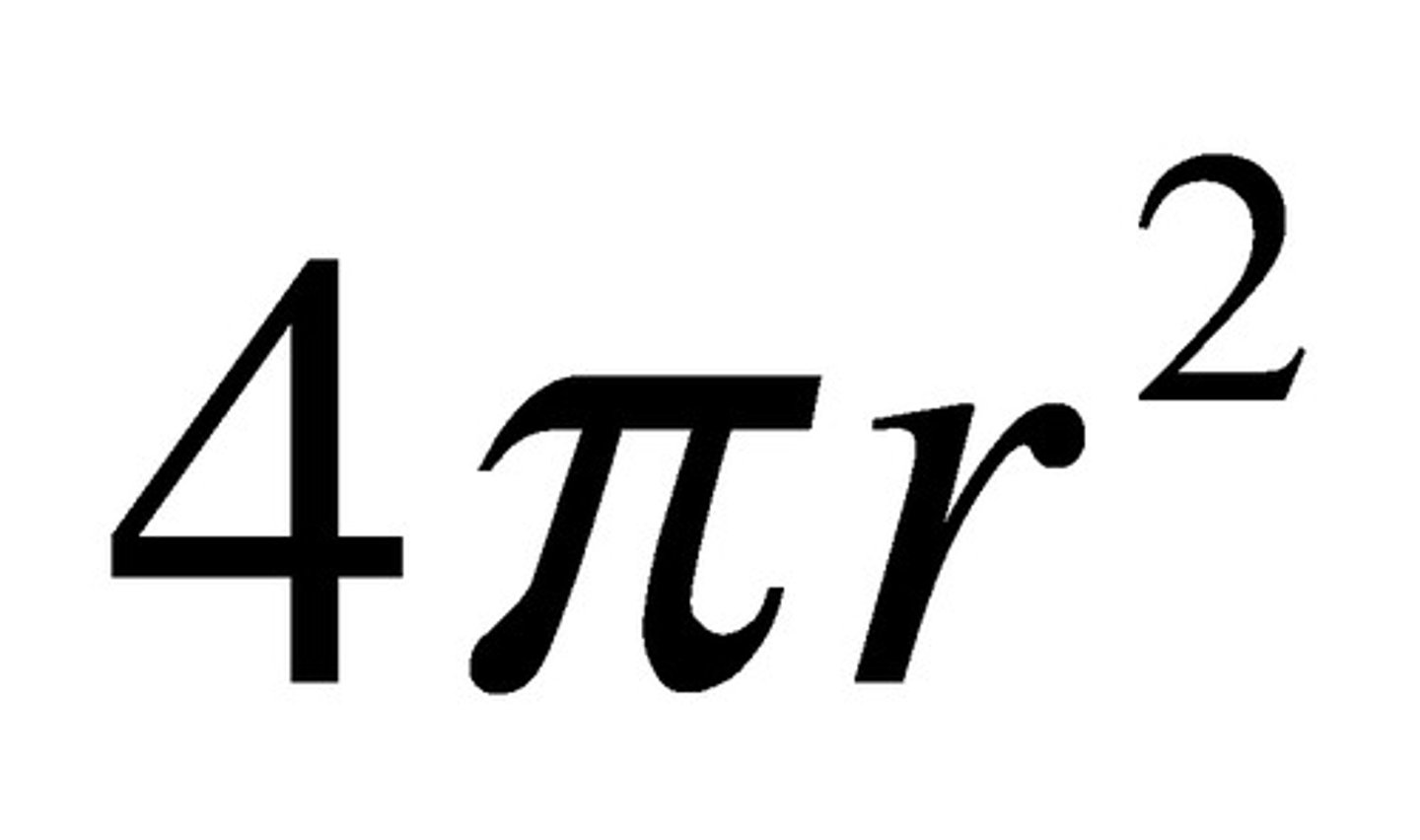
Volume of Sphere

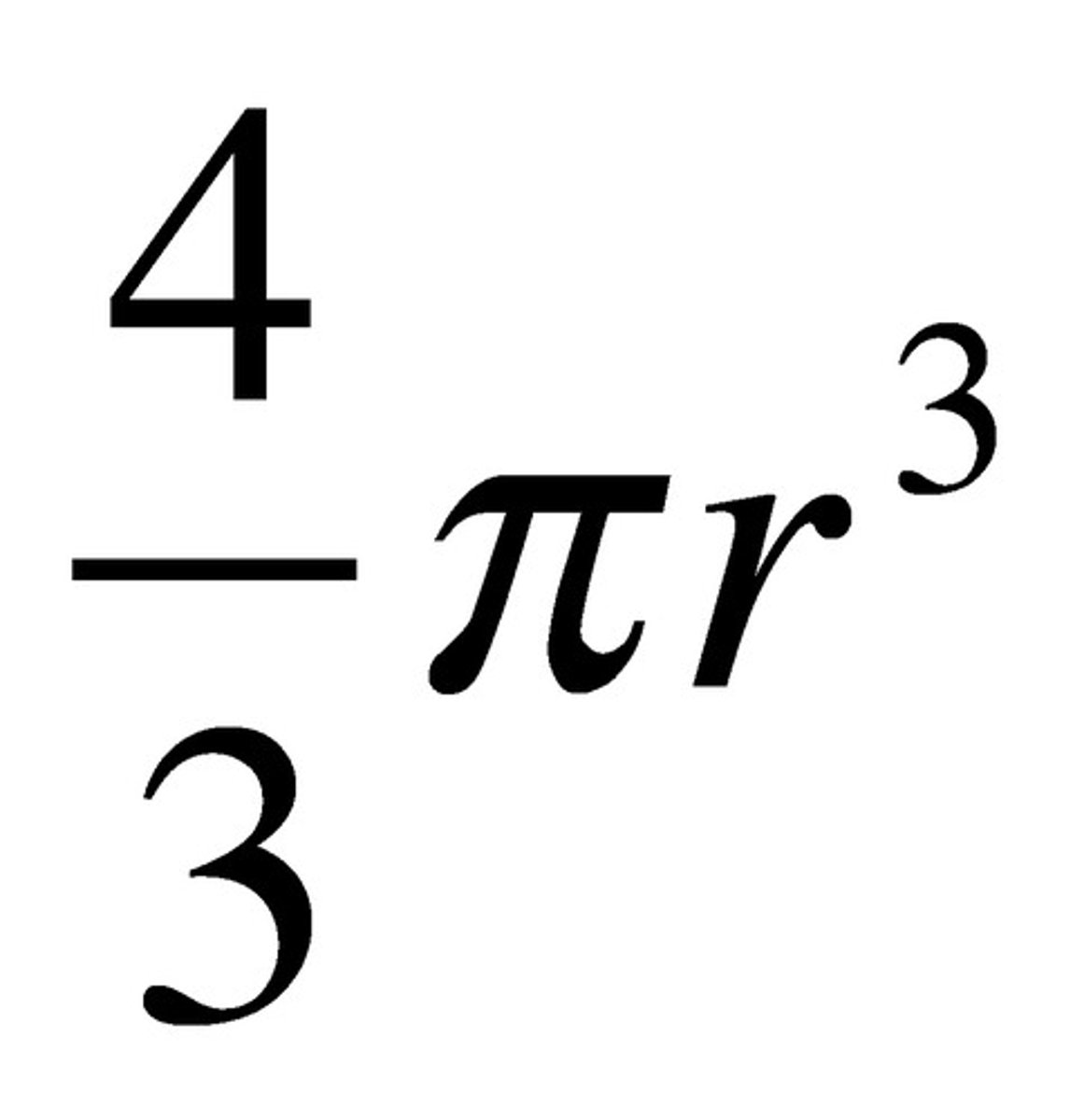
Surface Area of Cylinder

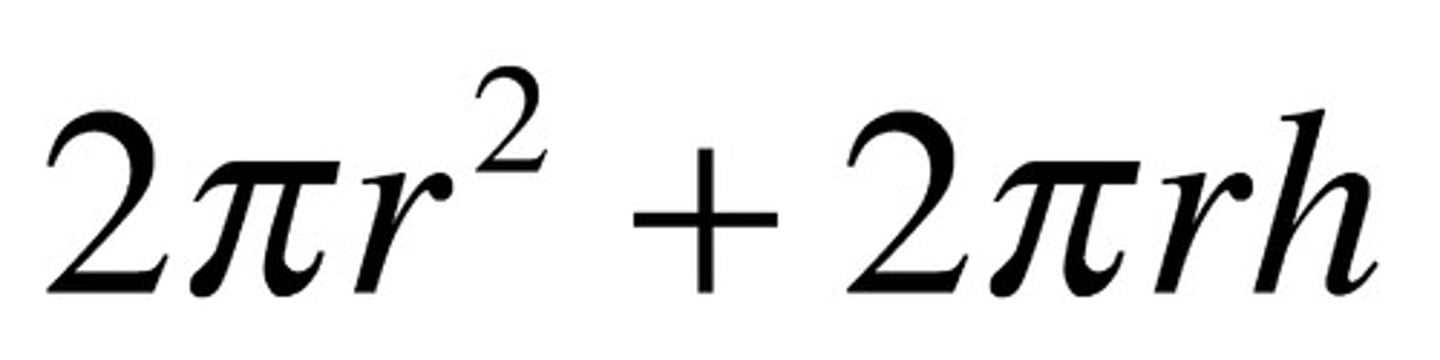
Volume of Cylinder

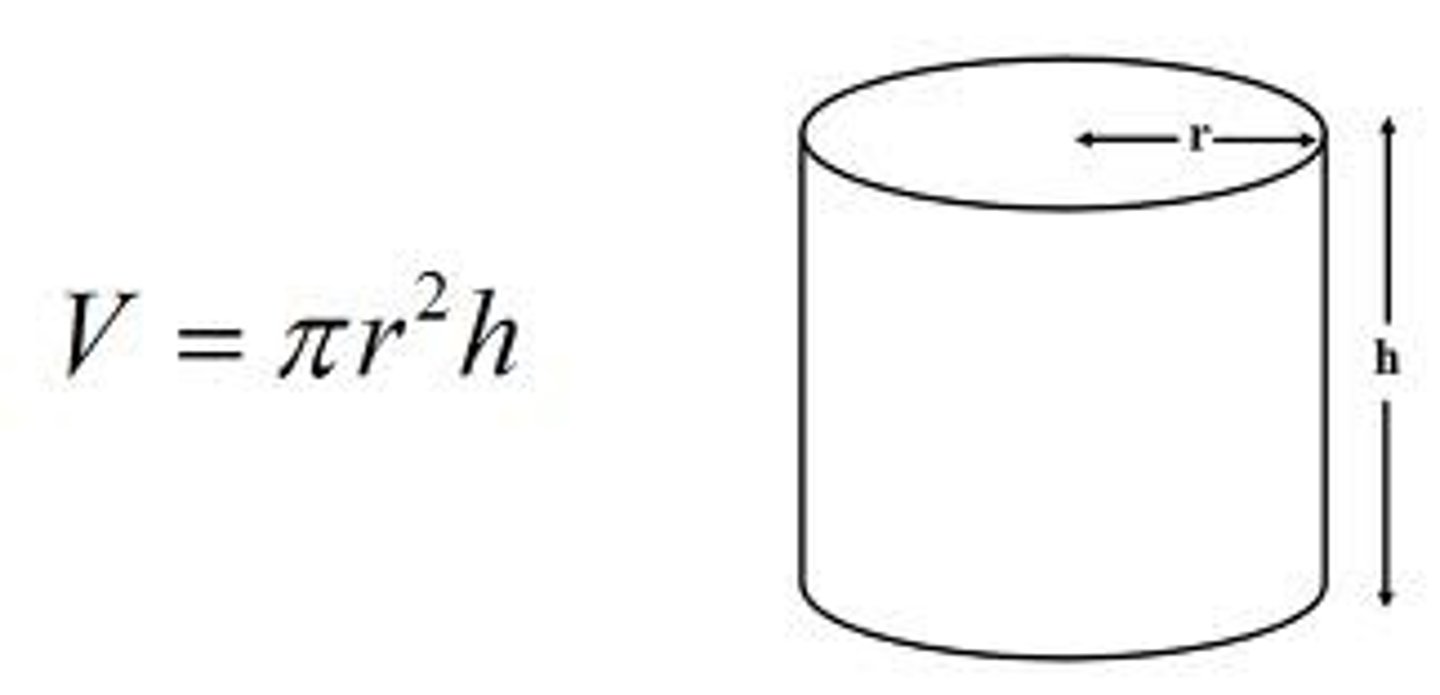
Surface Area of Cube

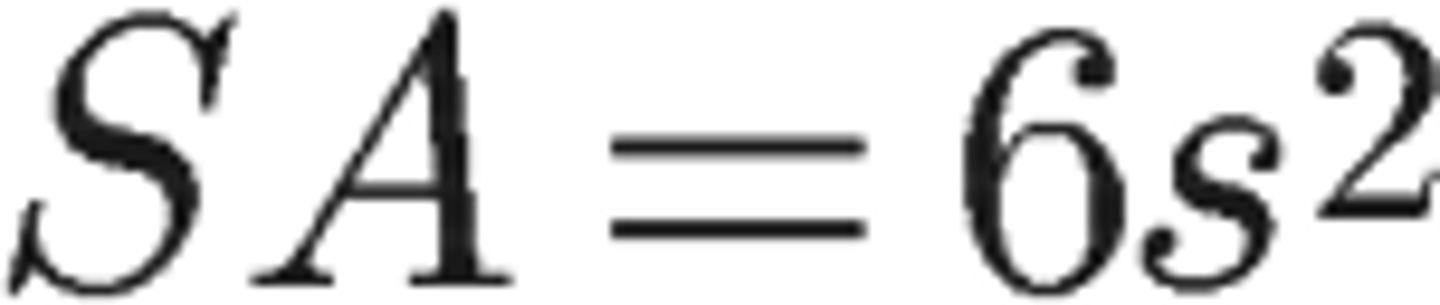
Volume of Cube

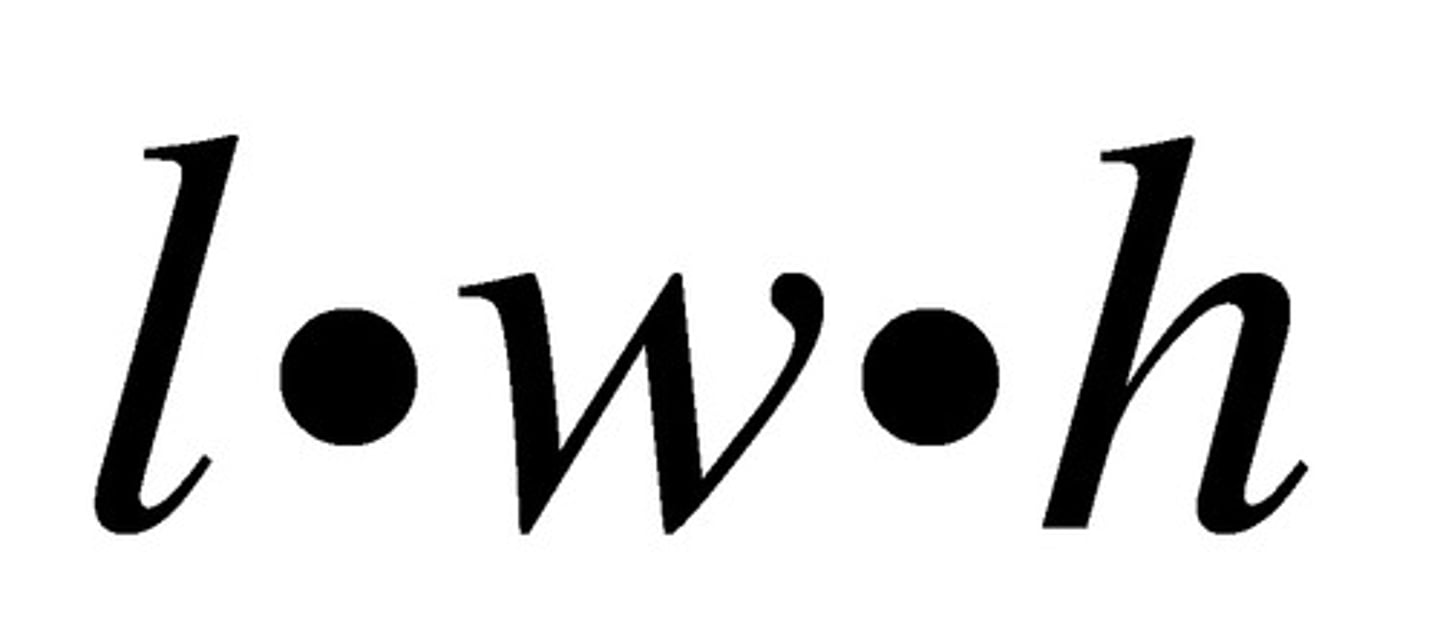
Area of Circle

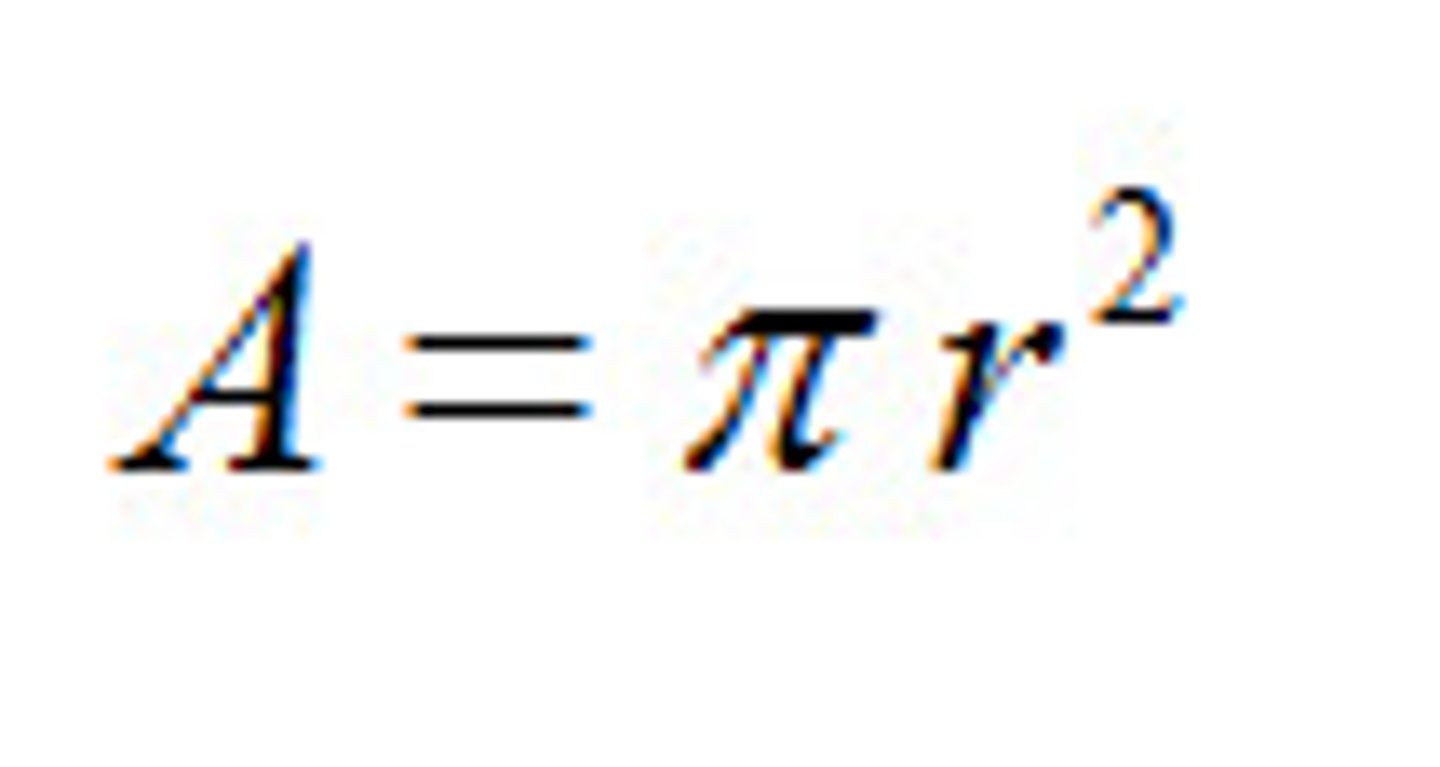
Perimeter of Circle

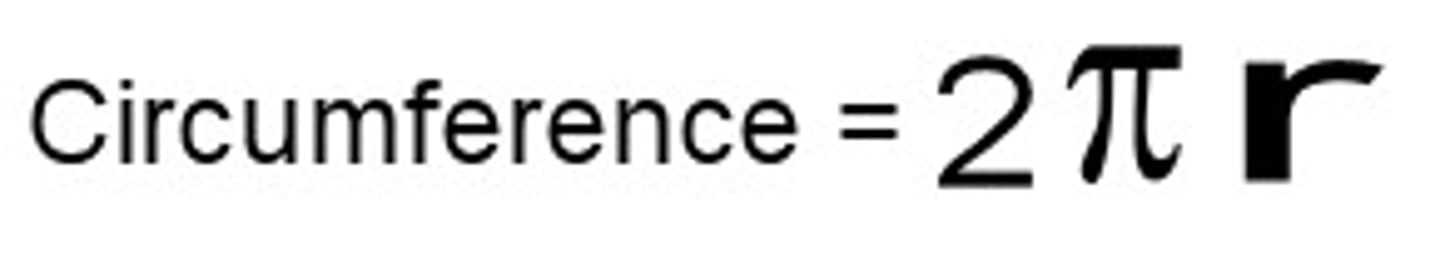
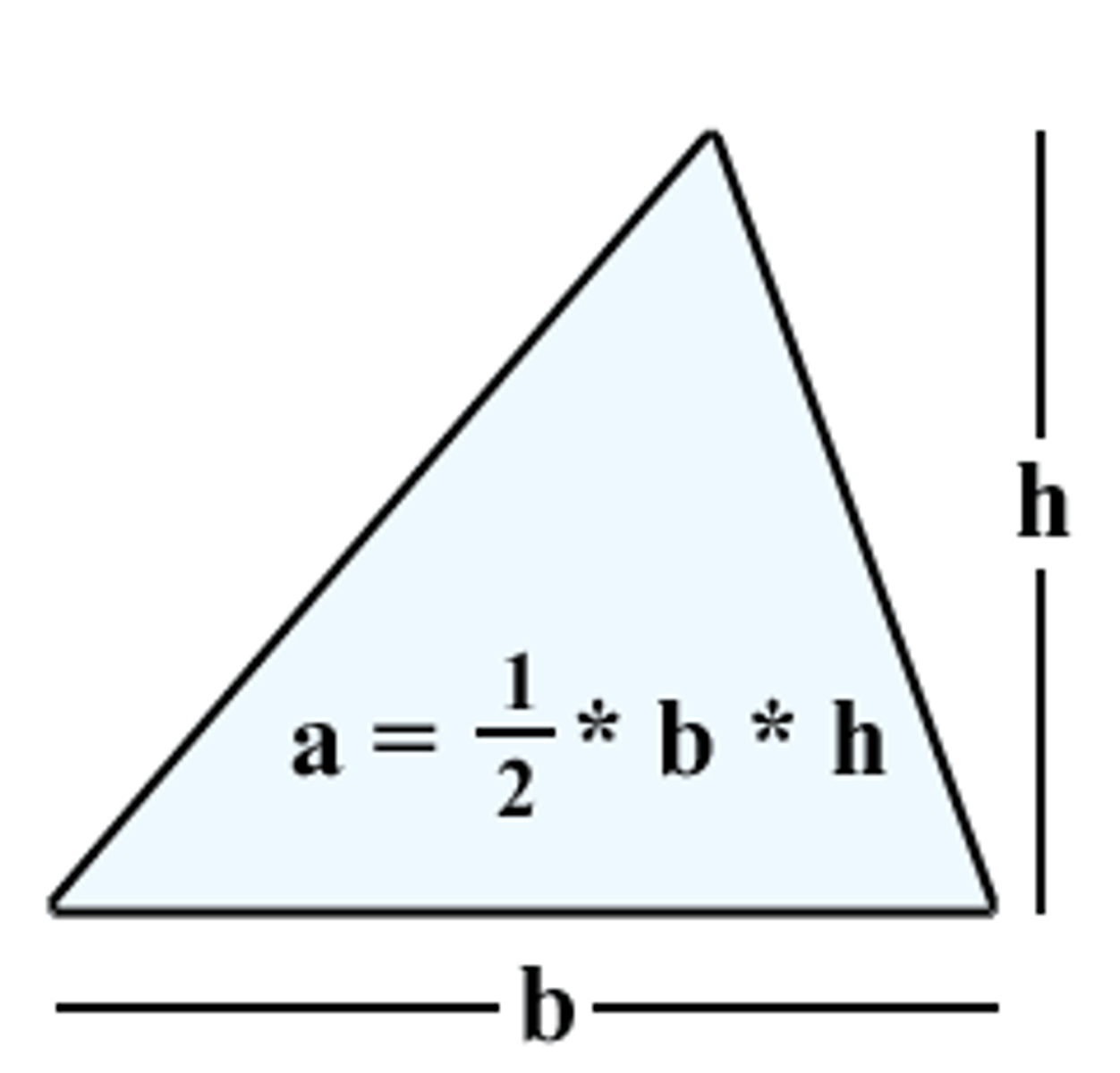
Area of Triangle

Perimeter of Triangle

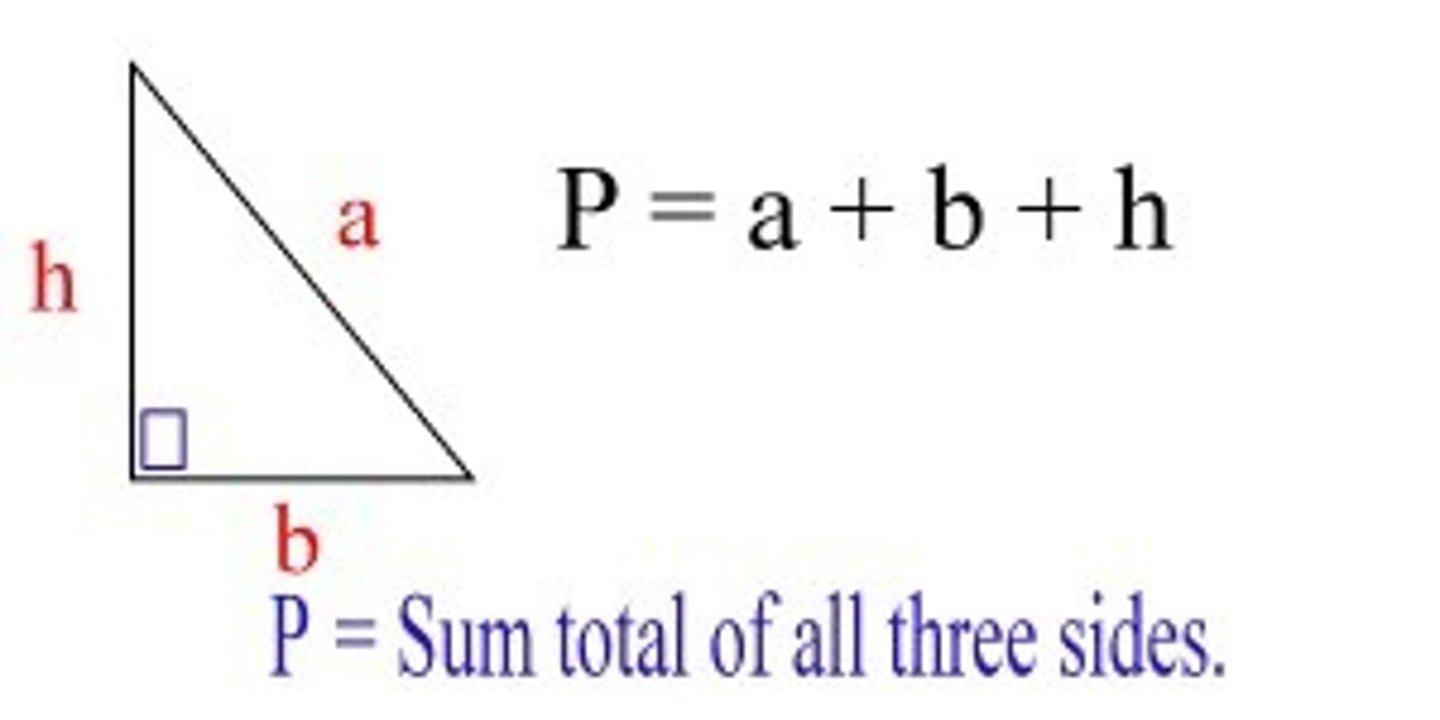
Area of Rectangle

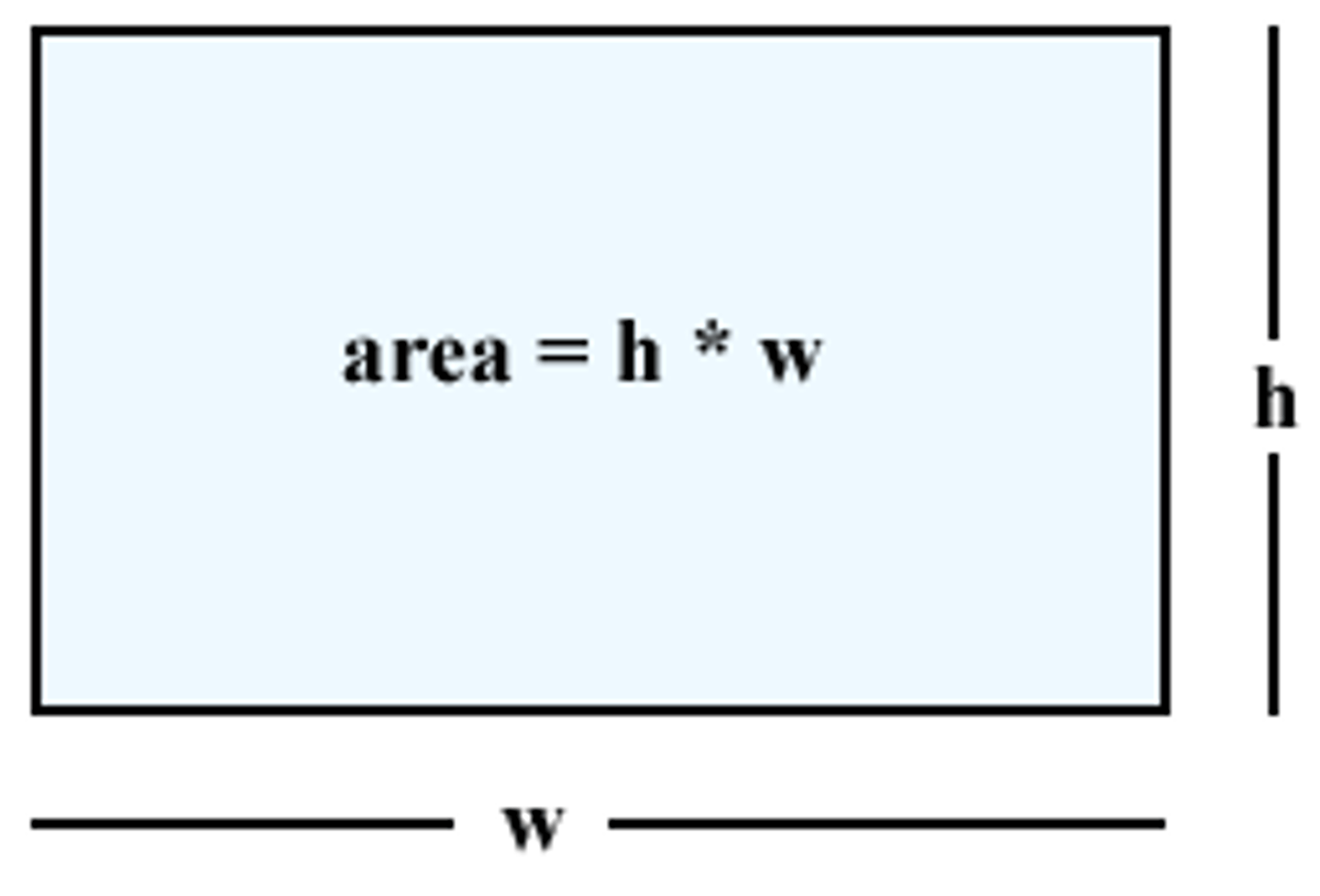
Perimeter of Rectangle

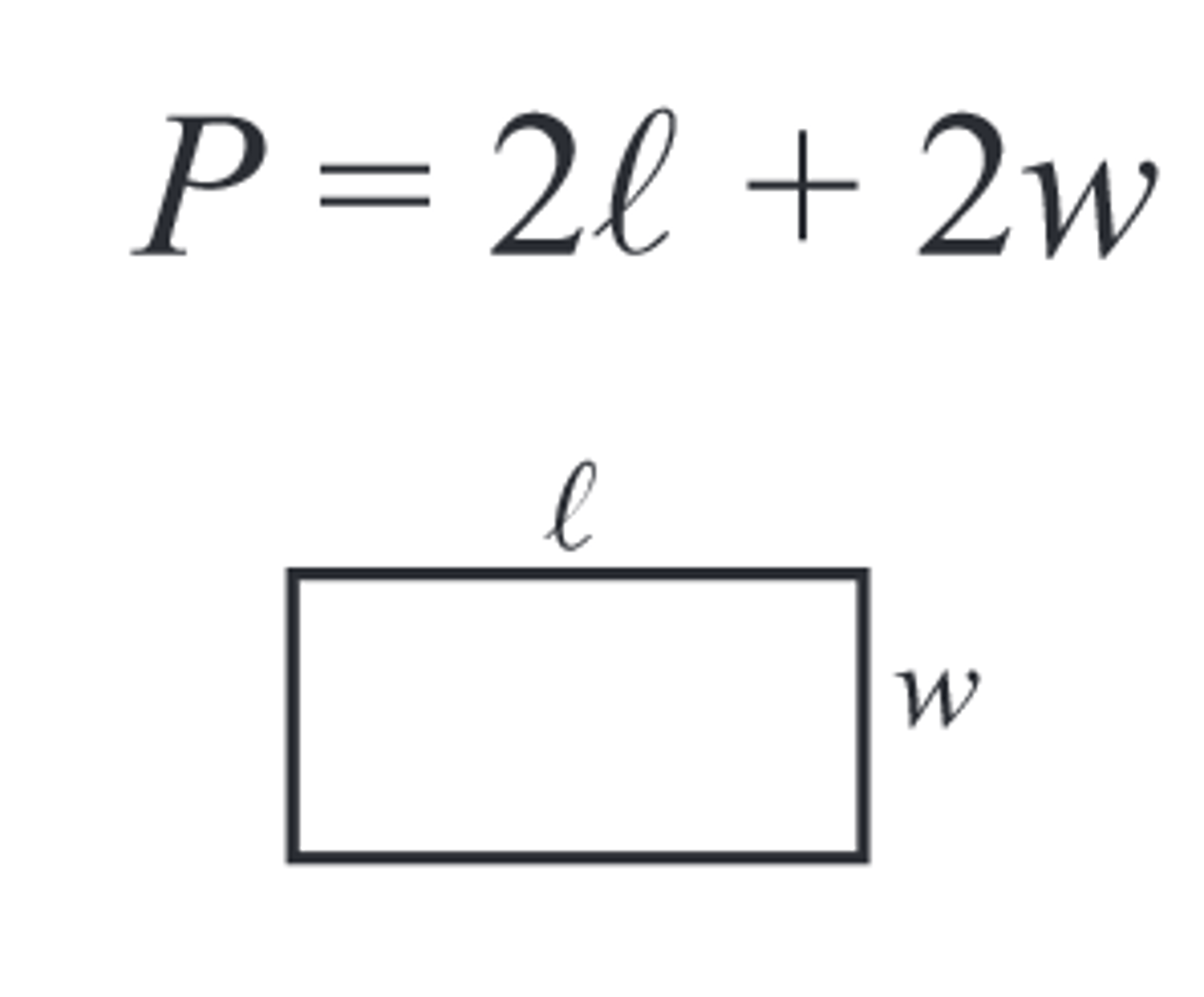
Area of Sector

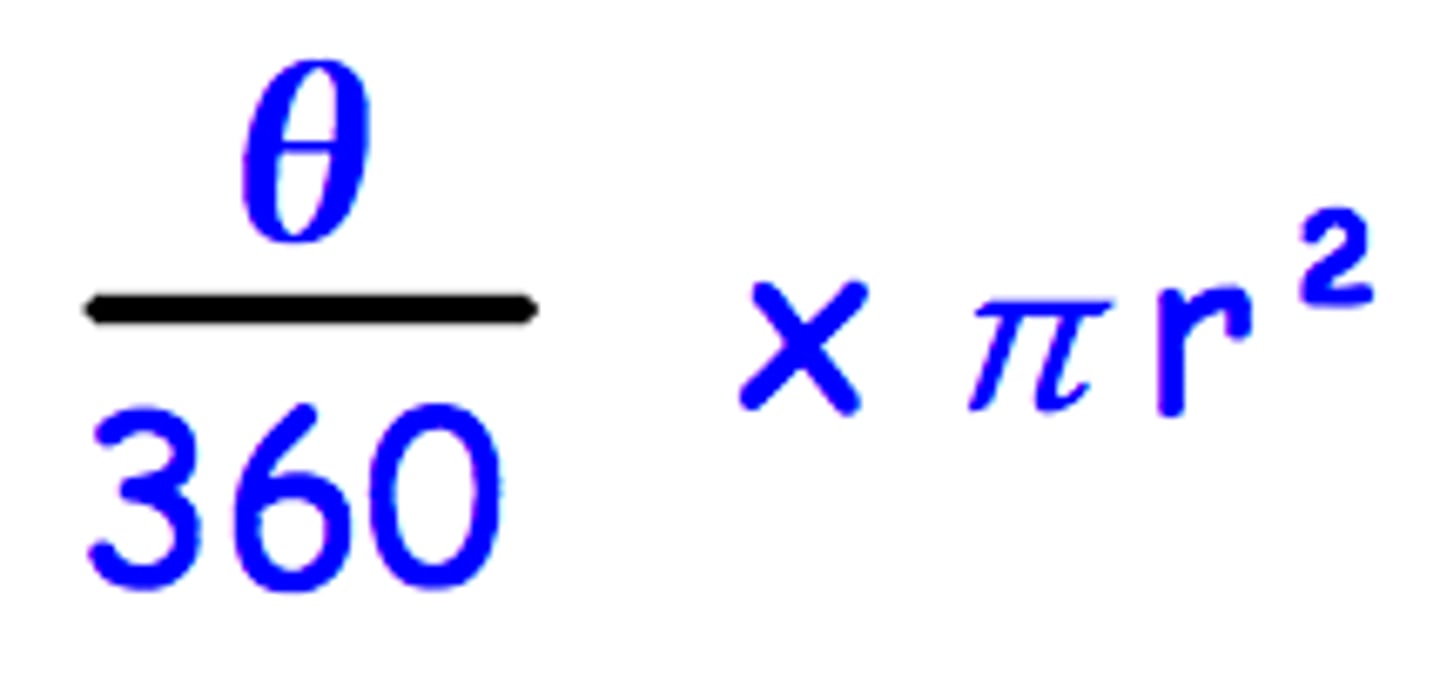
Perimeter of Sector

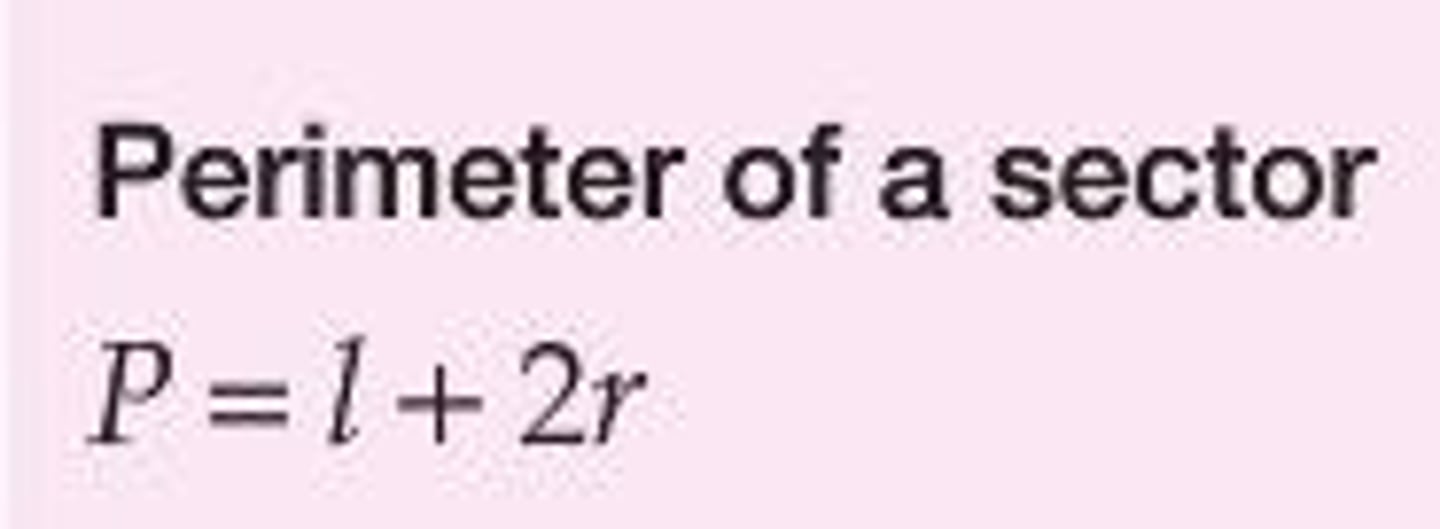
Distance Formula

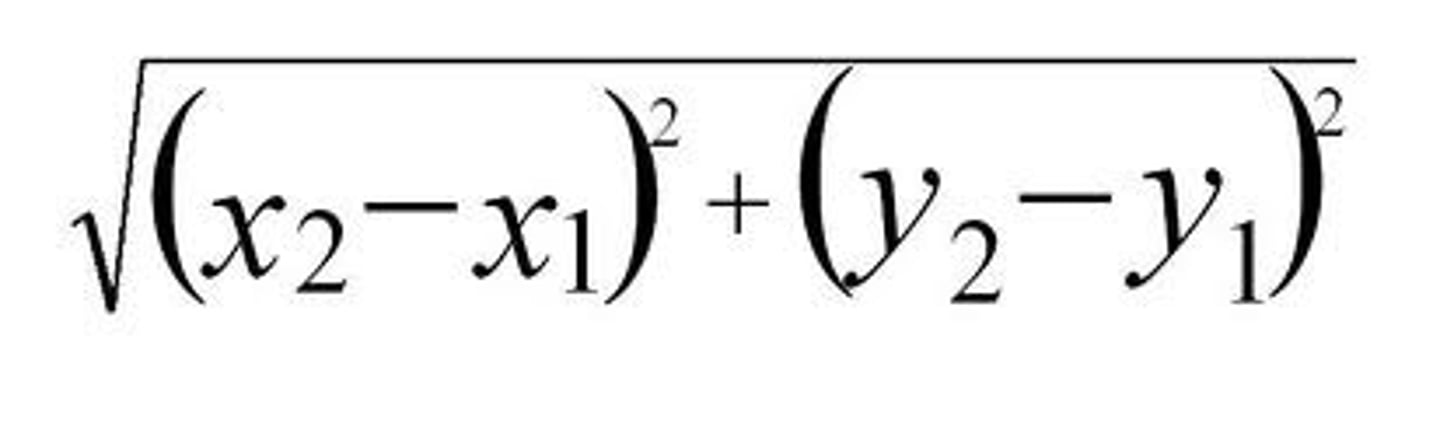
Pythagorean Theorem

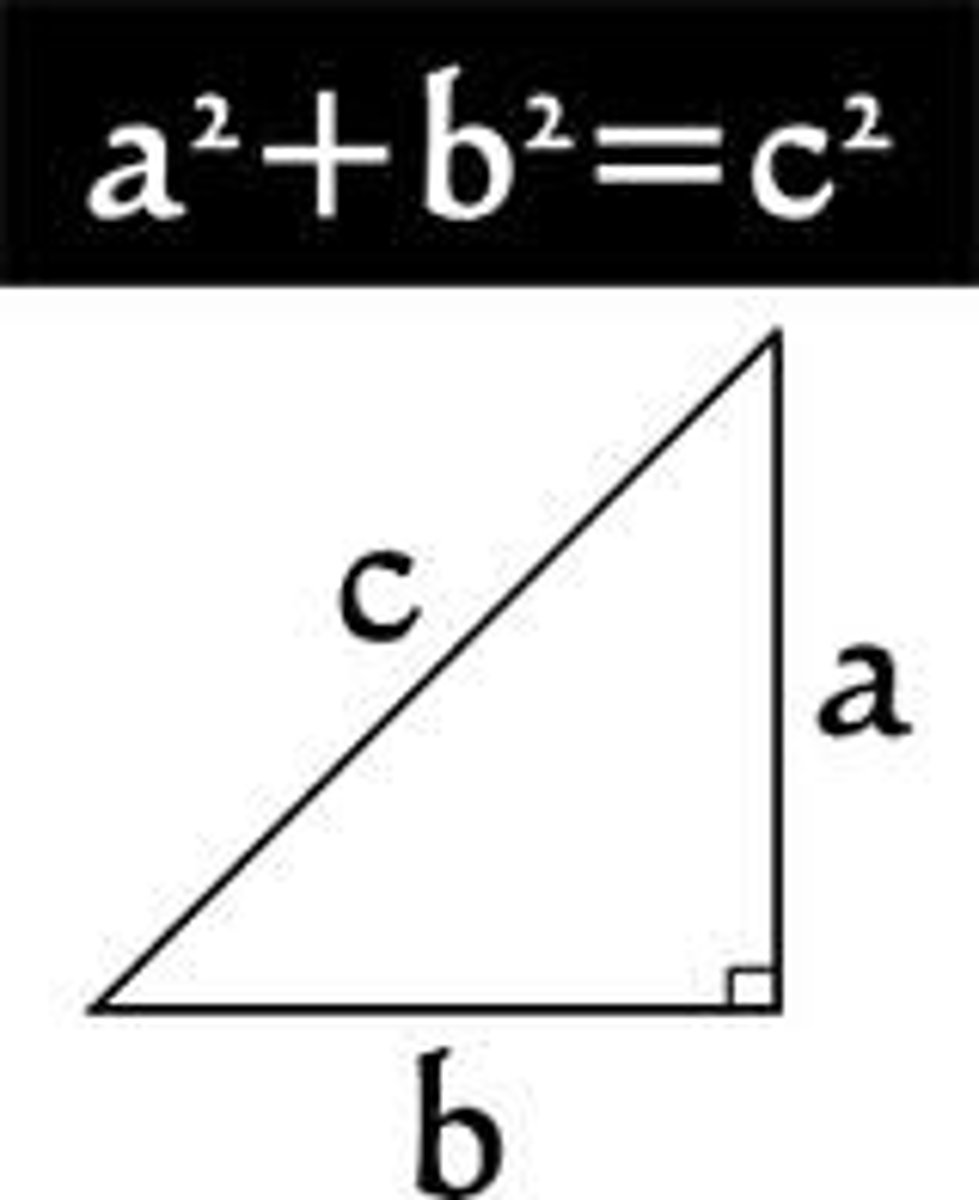
Properties of Logarithmic Functions

(See Cheat Sheet)

Properties of Exponential Functions

(See Cheat Sheet)

Trigonometric Identities

(See Cheat Sheet)

Limits

(See Cheat Sheet)

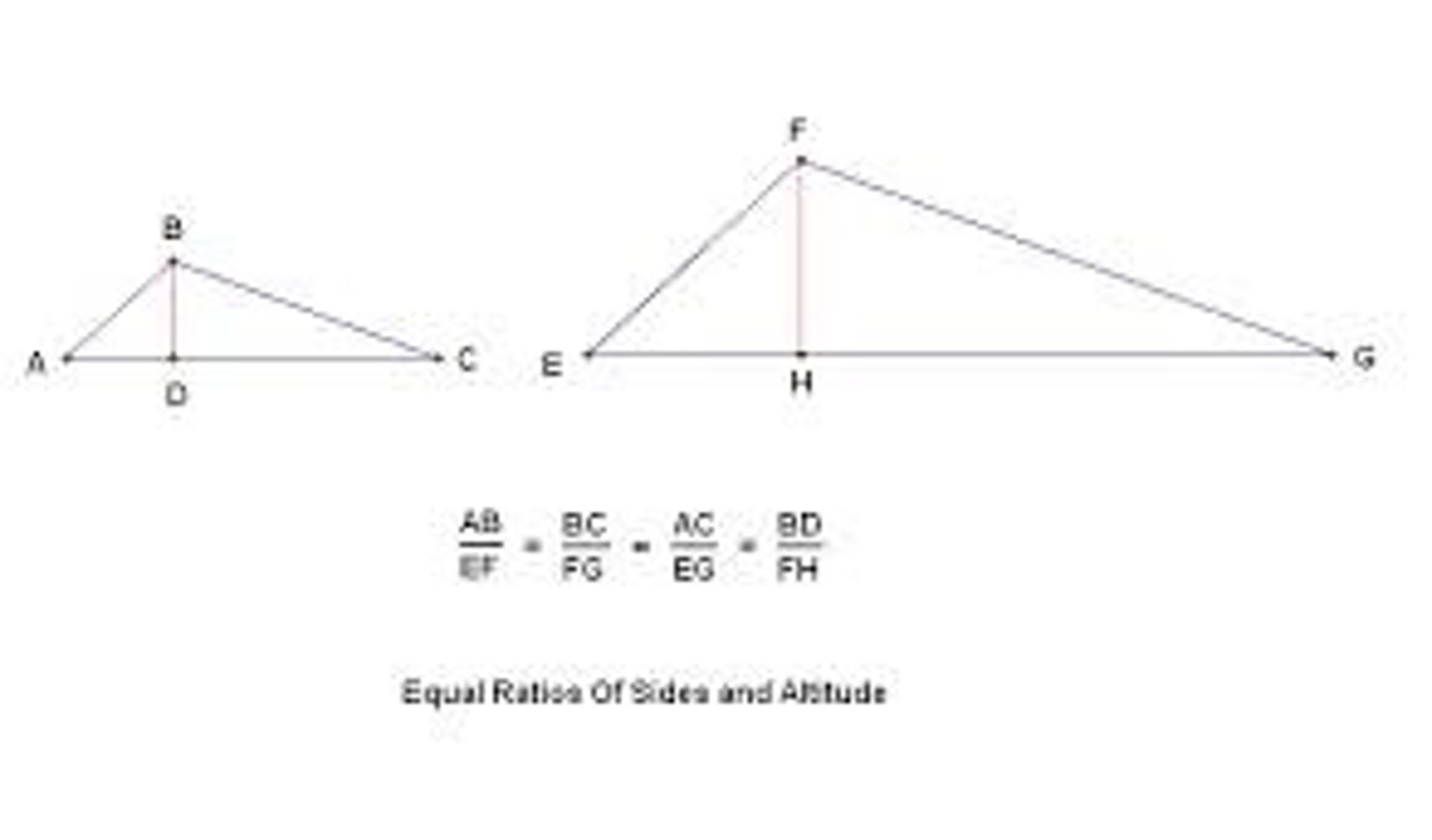
Properties of Similar Triangles

Derivatives

(See Cheat Sheet)

Applications of Derivatives

(See Cheat Sheet)

Integration

(See Cheat Sheet)

Rolle's Theorem

Suppose y=f(x) is a continuous function on [a,b] and differentiable on the interior (a,b), then there is a tleast one number in (a,b) such that f'(c)=0.

Intermediate Value Theorem

If f is continuous on [a,b] and k is a number between f(a) and f(b), then there exists at least one number c such that f(c)=k