FM Formula Sheet

Flashcards on FM Formulas

Effective Rate of Interest (𝑖)

The effective rate of interest, denoted as i, represents the actual rate of return on an investment or loan over a one-year period. It takes into account the effects of compounding.

\frac{A(t) - A(t-1)}{A(t-1)}

Effective Rate of Discount (𝑑)

The effective rate of discount, denoted as d, is the actual rate at which interest is discounted from the future value of an investment or loan to determine its present value. It is the ratio of the interest amount to the amount at time t.

\frac{A(t) - A(t-1)}{A(t)}

Amount Function 𝐴(𝑡) vs Accumulation Function a(t)

The amount function, A(t), represents the amount to which an initial investment of A(0) accumulates by time t. It is the product of the initial investment amount at time 0, A(0), and the accumulation function, a(t) .

A(0) \cdot a(t)

All-in-One Relationship Formula, accumulation to time t under i, i(m), d, d(m) and 𝛿

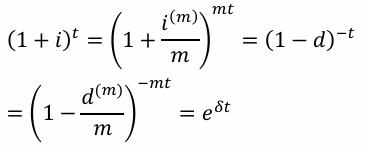
Variable Force of Interest 𝛿

The force of interest, denoted as \delta, is the instantaneous rate of interest at time t. It can be variable and is defined as the derivative of the accumulation function divided by the accumulation function itself.

\frac{a'(t)}{a(t)}

Accumulate 1 from time 0 to t under 𝛿(t)

This formula calculates the accumulation of an initial investment of 1 from time 0 to time t under a variable force of interest \delta(s). It involves integrating the force of interest function over the time interval [0, t] and then taking the exponential of the result.

exp \left[ \int_{0}^{t} \delta(s) \, ds \right]

Discount Factor 𝑣

The discount factor, denoted as v, is the present value of 1 unit of currency to be paid one year in the future. It is related to the effective interest rate i and the effective discount rate d.

\frac{1}{1 + i} = 1 - d

Discount RATE 𝑑

The discount rate, denoted as d, is the rate at which interest is deducted in advance from the future value of an investment or loan. It is related to the effective interest rate i.

\frac{i}{1 + i}

Inflation & the Real Interest Rate i_{real}

This formula calculates the real interest rate (i_{real}) taking into account the effects of inflation (\pi). It represents the actual increase in purchasing power from an investment after adjusting for inflation.

\frac{1 + i}{1 + \pi} - 1

Interest Rate Formula

This formula calculates the nominal interest rate (i) based on the real interest rate (i_{real}) and the inflation rate (\pi).

(1 + i_{real})(1 + \pi) - 1

Annuity-Immediate PV = a_{\overline{n}\|}

An annuity-immediate is a series of payments made at the end of each period. The present value (PV) of an n-year annuity-immediate, denoted as a_{\overline{n}\|}, is the sum of the present values of each payment.

v + v^2 + \cdots + v^n = \frac{1 - v^n}{i}

Annuity-Immediate AV = s_{\overline{n}\|}

An annuity-immediate is a series of payments made at the end of each period. The accumulated value (AV) of an n-year annuity-immediate, denoted as s_{\overline{n}\|}, is the sum of the accumulated values of each payment.

1 + (1 + i) + \cdots + (1 + i)^{n-1} = \frac{(1 + i)^n - 1}{i}

Annuity-Due PV = \ddot{a}_{\overline{n}\|}

An annuity-due is a series of payments made at the beginning of each period. The present value (PV) of an n-year annuity-due, denoted as \ddot{a}_{\overline{n}\|}, is the sum of the present values of each payment.

1 + v + v^2 + \cdots + v^{n-1} = \frac{1 - v^n}{d}

Annuity-Due AV = \ddot{s}_{\overline{n}\|}

An annuity-due is a series of payments made at the beginning of each period. The accumulated value (AV) of an n-year annuity-due, denoted as \ddot{s}_{\overline{n}\|}, is the sum of the accumulated values of each payment.

(1 + i) + (1 + i)^2 + \cdots + (1 + i)^n = \frac{(1 + i)^n - 1}{d}

Immediate vs. Due \ddot{a}_{\overline{n}\|} , a_{\overline{n}\|} and \ddot{s}_{\overline{n}\|} , s_{\overline{n}\|} relationships

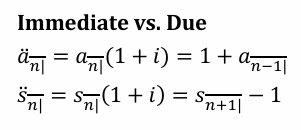
m-year deferred n-year annuity-immediate

This represents the present value of an n-year annuity-immediate deferred by m years. It is equivalent to the present value of an (m+n)-year annuity-immediate minus the present value of an m-year annuity-immediate.

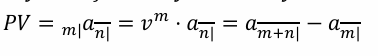
Perpetuity-immediate PV = a_{\overline{\infty}\|}

A perpetuity-immediate is a series of payments that continue indefinitely, with payments made at the end of each period. The present value (PV) of a perpetuity-immediate, denoted as a_{\overline{\infty}\|}, is the sum of the present values of each payment.

v + v^2 + \cdots = \frac{1}{i}

Perpetuity-due: PV = \ddot{a}_{\overline{\infty}\|}

A perpetuity-due is a series of payments that continue indefinitely, with payments made at the beginning of each period. The present value (PV) of a perpetuity-due, denoted as \ddot{a}_{\overline{\infty}\|}, is the sum of the present values of each payment.

1 + v + v^2 + \cdots = \frac{1}{d}

This formula relates the present value of a perpetuity-due to the present value of a perpetuity-immediate.

1+a_{\overline{\infty}\|}=\ddot{a}_{\overline{\infty}\|}

PV of n-year annuity-immediate with payments of 𝑃, 𝑃 + 𝑄, 𝑃 + 2𝑄, … , 𝑃 + (𝑛 − 1)𝑄

This formula calculates the present value of an n-year annuity-immediate with payments that increase arithmetically. The payments start at P and increase by Q each period.

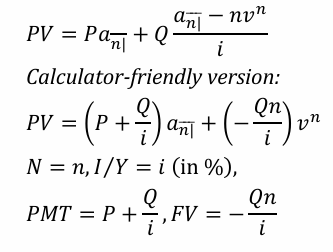
Unit increasing: (Ia)_{\overline{n}\|}

This represents the present value of a unit increasing annuity, where the payments increase by 1 each period.

\frac{\ddot{a}_{\overline{n}\|} - nv^n}{i}

Unit decreasing: (Da)_{\overline{n}\|}

This represents the present value of a unit decreasing annuity, where the payments decrease by 1 each period.

\frac{n - a_{\overline{n}\|}}{i}

PV of perpetuity-immediate and perpetuity-due with payments of 1, 2, 3, … (Ia)_{\overline{\infty}\|}

This formula calculates the present value of a perpetuity-immediate with payments increasing arithmetically, starting at 1 and increasing by 1 each period.

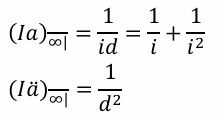
(I\ddot{a})_{\overline{\infty}\|}

This formula calculates the present value of a perpetuity-due with payments increasing arithmetically, starting at 1 and increasing by 1 each period.

\frac{1}{d^2}

PV of an n-year annuity-immediate with payments of 1, (1 + 𝑘), (1 + 𝑘)^2, … , (1 + 𝑘)^(n-1)

This formula calculates the present value of an n-year annuity-immediate with payments that increase geometrically. The payments start at 1 and increase by a factor of (1 + k) each period. Or do the (1 - omitted term)/(1 - common ratio) method.

\frac{1 - (\frac{1 + k}{1 + i})^n}{i - k}

Level and Increasing Continuous Annuity \bar{a}_{\overline{n}\|}

This formula calculates the present value of a level continuous annuity, where payments are made continuously over the term of the annuity.

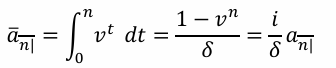
Level and Increasing Continuous Annuity (I\bar{a})_{\overline{n}\|}

This formula calculates the present value of an increasing continuous annuity, where payments increase continuously over the term of the annuity.

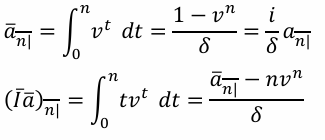
Internal Rate of Return (IRR)

Internal Rate of Return (IRR) is the discount rate that makes the net present value (NPV) of all cash flows from a particular project equal to zero. The investment with the greatest IRR should be chosen.

The rate such that the present value of cash inflows is equal to the present value of cash outflows. Choose investment with greatest IRR.

Outstanding Balance Calculation Prospective: B_t

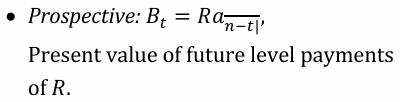
Outstanding Balance Calculation Retrospective: B_t

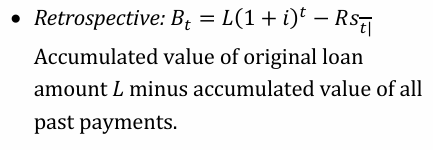
I_t

This formula calculates the interest portion (I_t) of the payment made at time t for an amortized loan. It is the product of the effective interest rate and the outstanding balance at time t-1.

i \cdot B_{t-1}

B_t

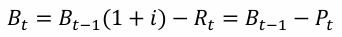
P_t

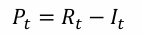
P_{t+k}

This formula relates the principal repaid at time t+k to the principal repaid at time t.

P_t(1 + i)^k

Basic Formula for price of bond 𝑃

This formula calculates the price (P) of a bond based on the present value of its coupon payments and redemption value.

Fra_{\overline{n}\|i} + Cv^n

Premium/Discount Formula for price of bond: 𝑃

This formula calculates the price (P) of a bond using the premium/discount formula, where C is the redemption value, Fr is the coupon payment, and i is the yield rate.

C + (Fr - Ci)a_{\overline{n}\|i}

Amortization Process Amount / Amount of Amortization

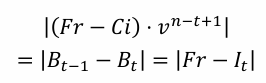
Book value (BOND): B_t

This formula calculates the book value (B_t) of a bond at time t, which is the present value of the remaining coupon payments and the redemption value. (PROSPECTIVE ONLY)

Fra_{\overline{n-t}\|i} + Cv^{n-t}

Interest earned

This formula calculates the interest earned at time t, which is the product of the yield rate and the book value at time t-1.

iB_{t-1}

How to Find Callable Bonds Price

Price of Callable Bond: calculate the LOWEST price for all possible redemption dates at a certain yield rate. This is the highest price that GUARANTEES this yield rate.

Macaulay Duration

Macaulay Duration is a measure of the weighted average time to receive the cash flows from a bond. It is calculated as the negative of the derivative of the bond price with respect to the force of interest, divided by the bond price.

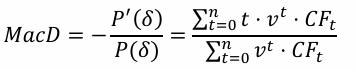
Modified Duration

Modified Duration is another measure of a bond's sensitivity to changes in interest rates. It is calculated as the negative of the derivative of the bond price with respect to the interest rate, divided by the bond price.

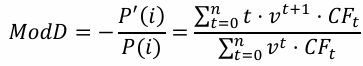
How to get ModD from MacD?

Modified duration can be expressed as the MacD multiplied by v.

MacD \cdot v

Interest, Principal Repaid at time t in a LOAN with n LEVEL payments

Duration of geometrically increasing perpetuity by k

This formula calculates the duration of a geometrically increasing perpetuity.

\frac{1 + i}{i - k}

Duration of 𝑛-year par bond

For an n-year par bond, the duration is equal to the present value of an annuity due.

\ddot{a}_{\overline{n}\|}

First-order Modified Approximation

This formula provides a first-order approximation of the change in bond price due to a change in interest rates, using the modified duration.

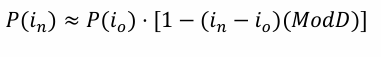
First-order Macaulay Approximation

This formula provides a first-order approximation of the change in bond price due to a change in interest rates, using the Macaulay duration.

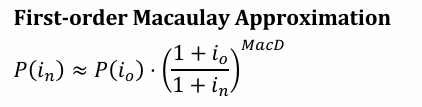
These 2 formulas describes how modified and macaulay duration changes with the passage of time, but cashflows remain the same.

Mac Convexity

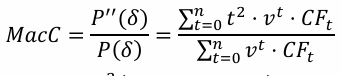
Mod Convexity

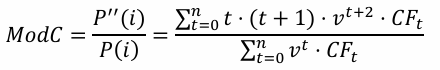
relationship btwn MacC & MacD

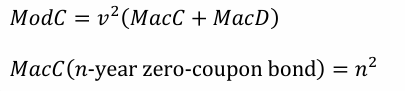
Immunization weight shortcut when there are 2 assets