Linear Regression From Scratch

How to create a Linear Regression ML model with only python and numpy.

Linear Regression Model with 1 Variable

The goal is to find the best w and b parameters that fit the data

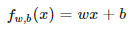
Cost Function for 1 variable Linear Regression Model

Find w and b that give you the smallest cost value. This gives you the parameters that best fit the data.

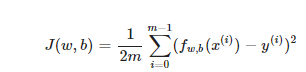
Model Prediction for 1 variable

Equation for a line, with an intercept b and a slope w.

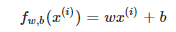
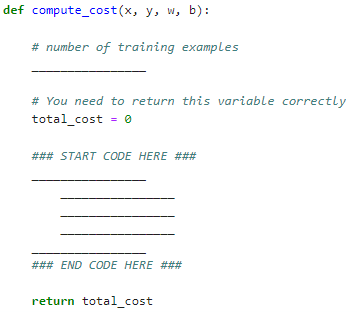
Exercise 1 objective: complete compute_cost

Iterate over the training examples for each example and compute,

• the prediction of the model for that example

• the cost for that example

• return the total cost over all examples

• what is m?

def compute_cost(x, y, w, b):

	# number of training examples

	__________________________

	# you need to return this variable correctly

	___________________________

	# start loop here

	____________________________

	return total_cost

def compute_cost(x, y, w, b): 

    # number of training examples
    m = x.shape[0] 
    
    # You need to return this variable correctly
    total_cost = 0
    
    # start loop here
    for i in range(m):
        f_wb = w*x[i] + b
        cost = (f_wb - y[i])**2
        total_cost += cost
    total_cost /= 2*m
    
    return total_cost

Gradient Descent Algorithm for parameters w and b for linear regression

parameters w and b are both updated simultaneously.

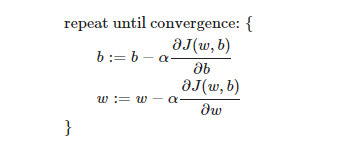
Derivative of

J(w,b)/db and J(w,b)/dw

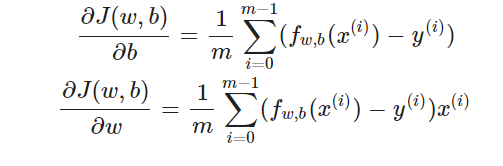
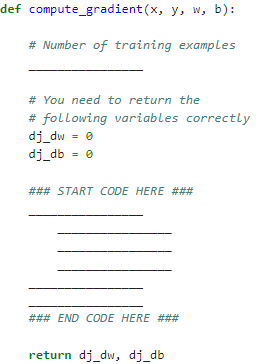
Exercise 2 objective: complete compute_gradient

iterate over the training examples and for each example compute:

• prediction of the model for that example

• gradient for parameters w and b for that example

• return total gradient update for all examples

def compute_gradient(x, y, w, b):

	# number of training examples

	_________________________

	# return the following variables correctly

	_________________________

	# start loop here

	_________________________

	#_____
	#_____

	return dj_dw, dj_db

def compute_gradient(x, y, w, b): 
   
    # Number of training examples
    m = x.shape[0]
    
    # return the following variables correctly
    dj_dw = 0
    dj_db = 0
    
    # start loop here
    for i in range(m):
        f_wb = w*x[i] + b
        dj_dw += (f_wb - y[i])*x[i]
        dj_db += f_wb - y[i]
    dj_dw /= m
    dj_db /= m
 
        
    return dj_dw, dj_db

Code

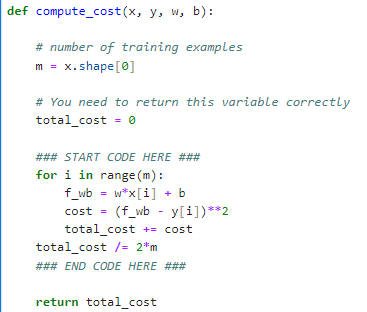
def compute_cost(x, y, w, b):

# number of training examples

____________________

# You need to return this variable correctly

total_cost = 0

### START CODE HERE ###

for i in range(m):

______________________

______________________

______________________

______________________

### END CODE HERE ###

return total_cost

def compute_cost(x, y, w, b):

# number of training examples

m = x.shape[0]

# You need to return this variable correctly

total_cost = 0

### START CODE HERE ###

for i in range(m):

f_wb = w*x[i] + b

cost = (f_wb - y[i])**2

total_cost += cost

total_cost /= 2*m

### END CODE HERE ###

return total_cost

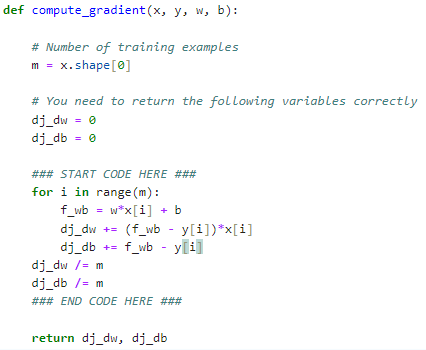
Code

def compute_gradient(x, y, w, b):

# Number of training examples

m = x.shape[0]

# You need to return the following variables correctly

dj_dw = 0

dj_db = 0

### START CODE HERE ###

for i in range(m):

f_wb = w*x[i] + b

dj_dw += (f_wb - y[i])*x[i]

dj_db += f_wb - y[i]

dj_dw /= m

dj_db /= m

### END CODE HERE ###

return dj_dw, dj_db