U6 Vocabulary - Circles

central angle

central angle

an angle made of two radii whose vertex is at the center of the circle

inscribed angle

an angle made of two intersecting chords whose vertex is on the circle

arc length

the length of an arc or portion of the circumference

sector

the portion of a circle enclosed by two radii and an arc

circle

the set of points in a plane equidistant from the center of the circle

circumference

the distance around the outside of a circle

pi

the ratio of the circumference of a circle to its diameter

chord

a segment whose endpoints lie on a circle

minor arc

an arc of a circle whose measure is less than 180 degrees

major arc

an arc of a circle whose measure is greater than 180 degrees

area of a circle

the amount of space occupied by a circle (A=πr²)

arc

a section of the circumference of a circle

tangent

a line in the plane of a circle that intersects the circle in exactly one point

secant

a line in the plane of the circle that intersects a circle in exactly two points

inscribed circle

a circle inside a polygon in which all sides of the polygon are tangent to the circle

radius

the distance from the center of a circle to any point on the circle

diameter

the distance across a circle through its center

point of tangency

the point at which a tangent line intersects a circle

semicircle

half of a circle

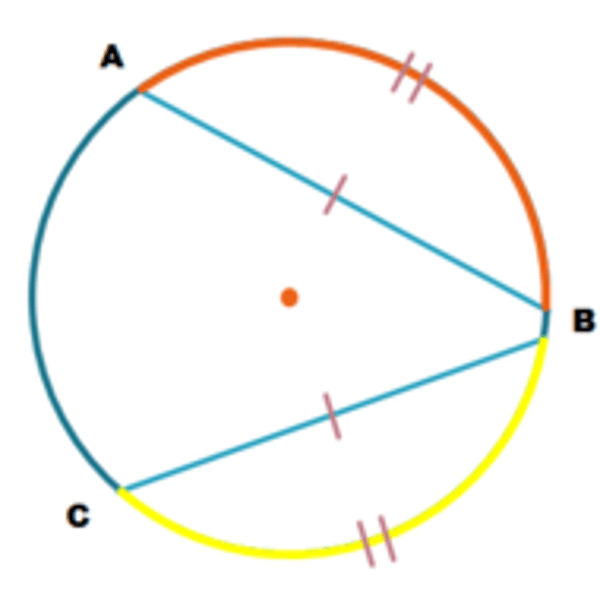
Chords and Arcs Theorem

In a circle, or in congruent circles, the arcs of congruent chords are congruent

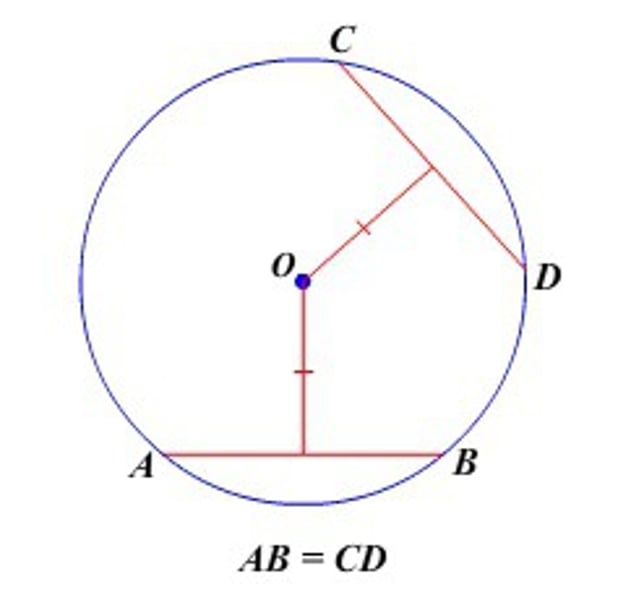
Chord Equidistance Theorem

In the same circle, or in congruent circles, two chords are congruent if and only if they are equidistant from the center.

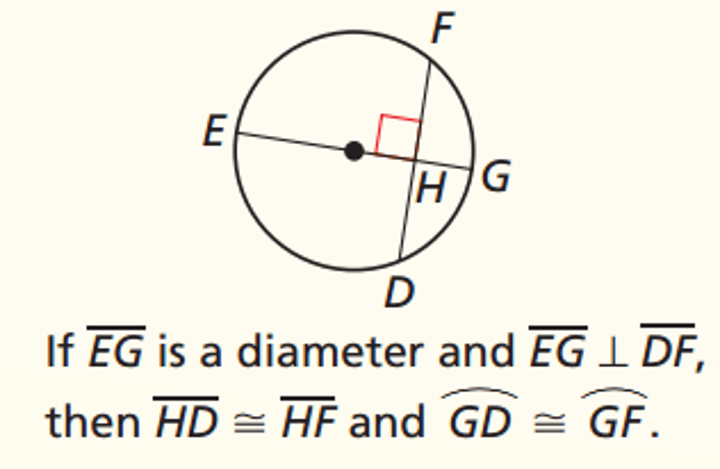
Chord Perpendicular Bisector Theorem

A diameter (or radius) perpendicular to a chord bisects the chord and its arc

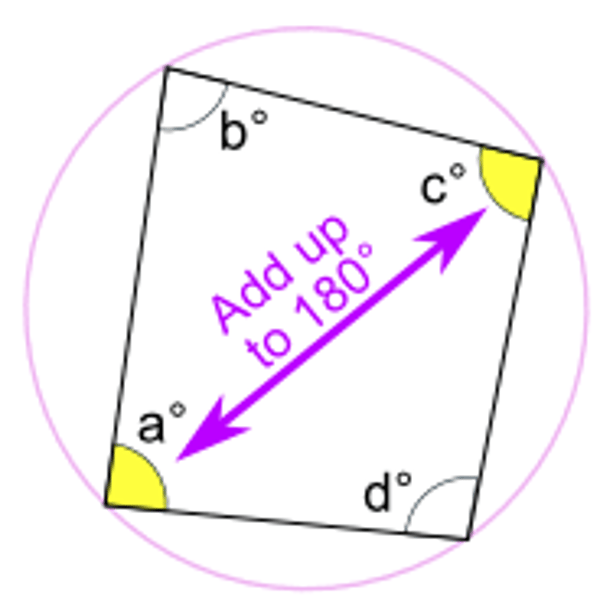
Quadrilateral inscribed in a circle

If a quadrilateral is inscribed in a circle, then its opposite angles are supplementary

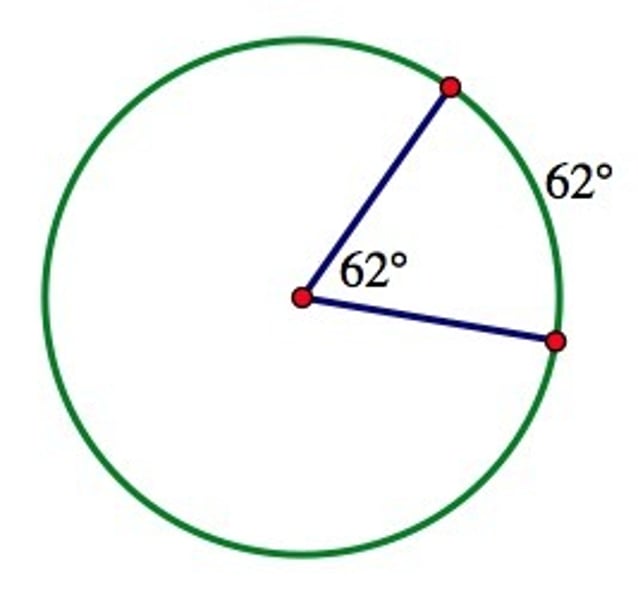
Central angle formula

angle=arc

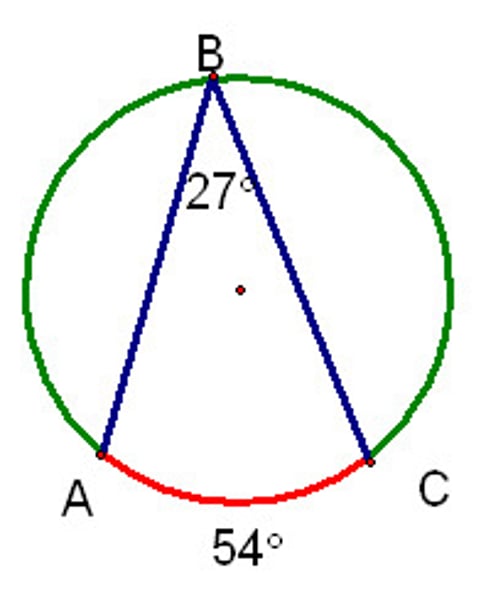
Inscribed angle formula

angle= 1/2(arc)

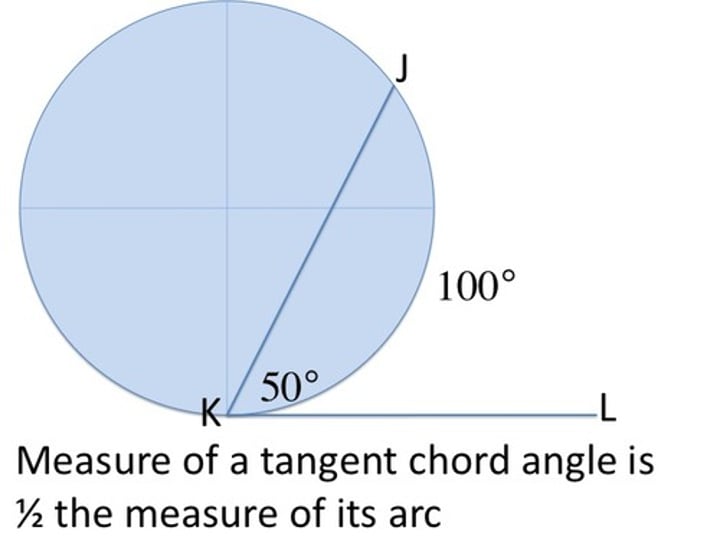
tangent inscribed angle formula

angle = 1/2(arc)

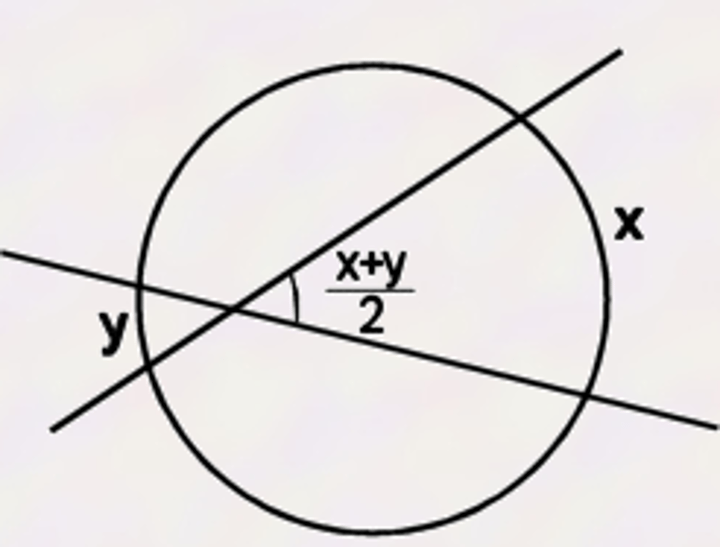
Formula to calculate angle formed inside of a circle by intersecting chords

(arc 1 + arc 2)/2

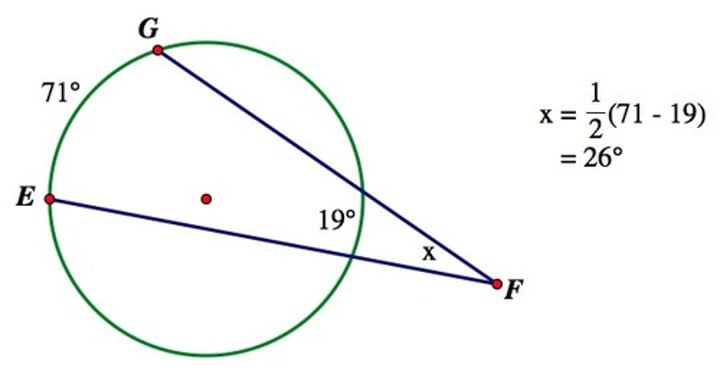
Formula to calculate angle formed outside of a circle by intersecting secants and tangents

angle = (big arc - small arc)/2

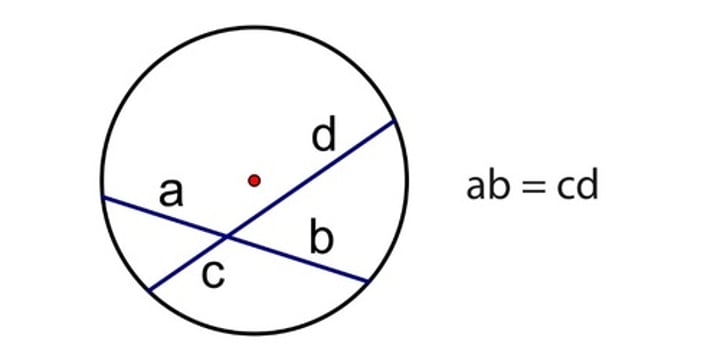
Formula to calculate chords' lengths if they intersect inside a circle

ab = cd

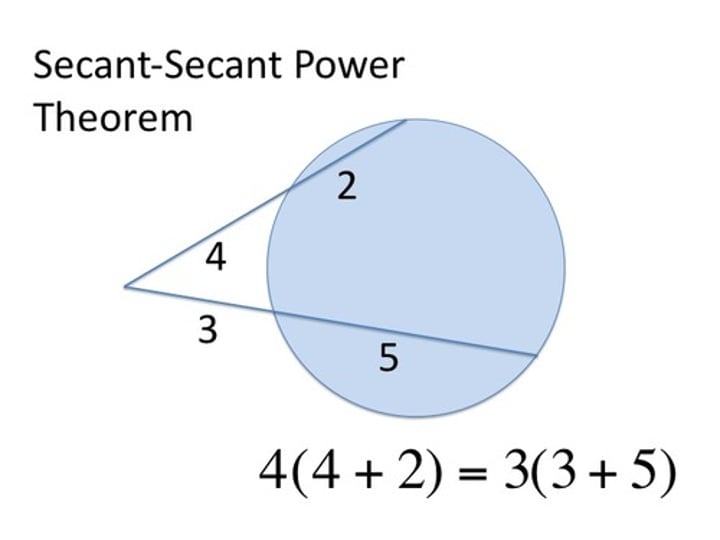
Formula to calculate secant and another secant length if they have a common endpoint outside of the circle

whole x outside = whole x outside

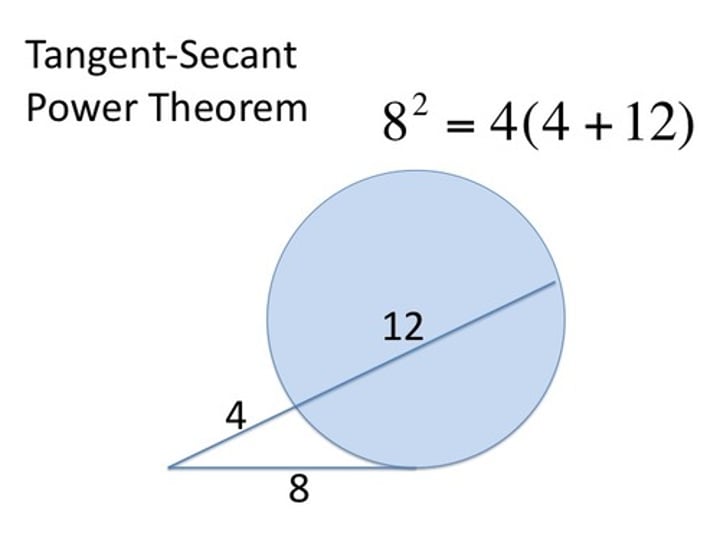
Formula to calculate secant or tangent length if they have a common endpoint outside of the circle

whole x outside = tangent squared

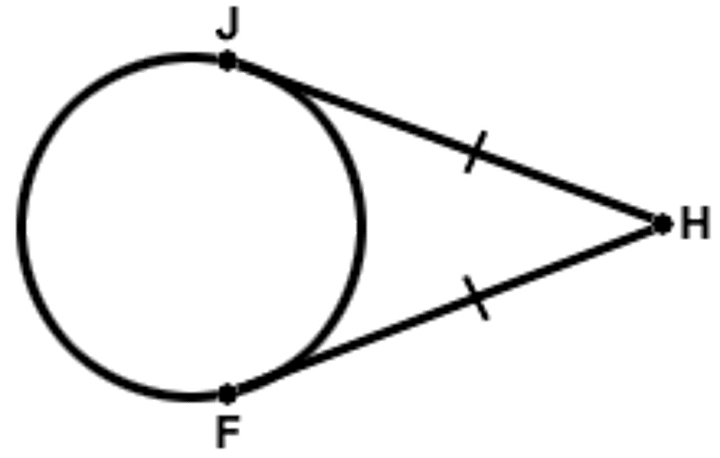
Formula to calculate 2 tangents length if they have a common endpoint outside of the circle

If two tangent segments are drawn to a circle from an external point, then those segments are congruent.

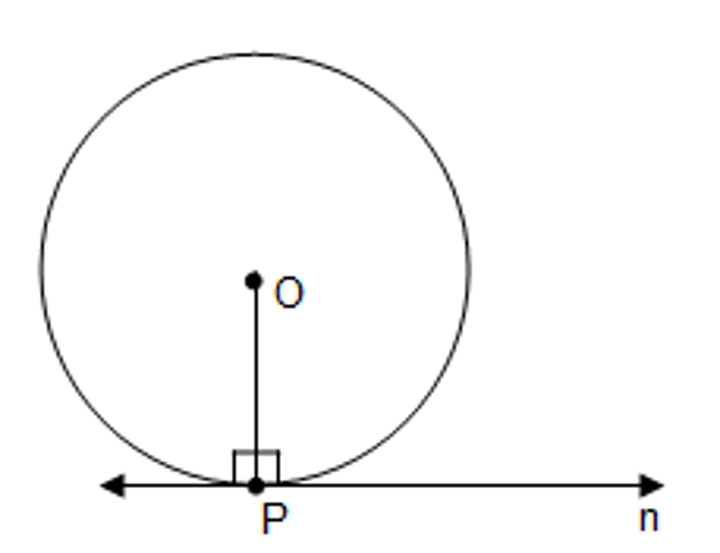
What relationship does a tangent line and a radius/diameter have?

If a line is tangent to a circle, then it is perpendicular to the radius drawn to the point of tangency

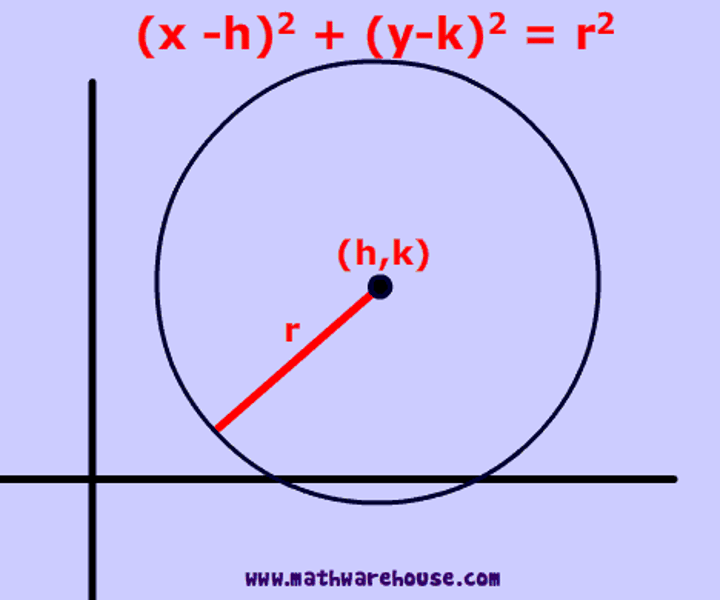
Equation of a circle

(x-h)²+(y-k)²=r², (h, k) is the center, r is the radius.