Algebra 1 Flashcards

We're so young, but we're on the road to ruin :(

The farther a slope is away from zero, the _______ it will be.

Narrower

Example: 10 will be 10 integers away from zero, compared to a slope of 1 (only one integer away). 10 will be narrower.

\
Same thing with negatives: -10 will be 10 integers away from zero. A slope of -1 will only be one integer away. -10 will be narrower.

The closer a slope is to zero, the _________ it will be.

Wider

Example: 10 will be 10 integers away from zero, compared to a slope of 1 (only one integer away). 10 will be narrower.

\
Same thing with negatives: -10 will be 10 integers away from zero. A slope of -1 will only be one integer away. -10 will be narrower.

How do you find c in completing a square?

b/2^2

How do we know if something if isn’t a function?

It doesn’t pass the Vertical Line Test/Has repeating x values.

What circle do you use for the greater than or equal to sign, and less than or equal to sign.

Closed

What circle do you use for the less than and greater than symbols?

Open

Transformation: INSIDE- positive ? negative?

Positive = Left

Negative = Right

Transformation: OUTSIDE- positive? negative?

Positive = Up

Negative = Down

Natural numbers are

Positive Integers

Commutative Property

The order doesn’t matter

Example: 5 + 4 = 4 + 5 = 9

Associative Property

Grouping doesn’t matter

Example: (1 + 2) + 3 = 1 + (2 + 3) = 6

Distributive Property

Numbers outside are multiplied by terms inside ()

Example: 3(x + y) = 3x + 3y

Additive Identity

Anything plus 0 equals itself.

Example: x + 0 = x

Multiplicative Identity

Anything times one is itself

Example: 1 \* x = x

Additive Inverse

When we add inverses, the sum is 0

Example: -2 + 2 = 0

Multiplicative Inverse

When we multiply inverses, the product is one.

Example: 4 times 1/4 = 1

What does FOIL stand for?

First, Outside, Inside, Last

Used when multiplying two binomials.

Ex: (x + y) (x + y)

Multiply the first numbers, then outside numbers, inside numbers, last numbers.

Lastly, add like terms.

How do you find if a solution is one a line?

Plug in the coordinates you are given to the solution you are also given.

What’s the purpose of point slope form?

To find the slope and a point on the graph.

What’s the formula for point slope form?

y - y1 = m(x - x1)

What is point intercept form?

y = mx + b

What’s the formula for rise over run/ slope?

m = y2 - y1/ x2 - x1

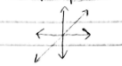
f(x) = x

Linear

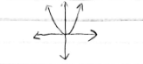
f(x) = x^2

Quadratic

f(x) = x^3

Cubic

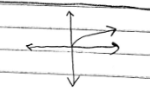
f(x) = √x

Square Root

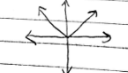
f(x) = | x |

Absolute Value

What kind of solution is this: x = 4

One solution

What kind of solution is this: -3 = -3

Infinite Solutions

What kind of solution is this? 5 = 6

No solutions

You cannot ____ exponents.

Add

Example: x^2 + x^3 doesn’t equal x^5

When using the calculator to determine if something is true or false… What number is false?

0

When using the calculator to determine if something is true or false… What number is true?

0

Graphing inequalities: If the sign eats y shade….

UP/ABOVE

Graphing inequalities: If you have

Dash the lines

How do you write set notation?

{variable symbol type of number | description}

example: {x € IR | x < 0}

When declarations are separated by “and”, ____ need to be correct to be true.

Both/All statements

When declarations are separated by “or”, ____ need to be correct to be true.

Only one of them

Intersecting Lines are what kind of solution?

One solution

Parallel Lines are what kind of solution?

No Solution

What does the same line say about what kind of solution we are looking at?

Infinite Solutions

How do you do Substitution?

1. Isolate y for one equation
2. Substitute y
3. Solve for x
4. Solve for y

How do you do Elimination?

1\.) Make sure the equations are lined up

2\.) Add or subtract the equations to eliminate the variable with common coefficients

3\.) Solve for the remaining variable

4\.) Substitute your answer into either original equation and solve for the other variable

Process to solve system of equation applications

1\.) Define your two variables

2\.) Write a system of equations using given information

3\.) Solve the system

4\.) Answer word-ly

Integer Sequences: How do I know if I’m looking at a linear sequence? What do we include in linear recursive formulas

Same 1st Differences; has a coefficient: n

Integer Sequences: How do I know if I’m looking at a quadratic sequence? What do we include in quadratic recursive formulas?

Same 2nd Differences; has a ^2 exponent (squared)

Integer Sequences: How do I know if I’m looking at a exponential sequence? What do we include in linear recursive formulas?

Same ratio (multiplying a constant number); has an exponent

Explicit Formulas: A1 means?

First term

Explicit Formulas: d means?

Difference