ALEVEL BIO WRITTEN PRAC

Enzyme rate experiments

carried out to determine the effect of a changing particular factor on the rate of a reaction.

Whats factors can be changed on enzyme rate experiment

• Temperature

• pH

• Enzyme concentration

• Substrate concentration

e key thing with enzyme rate experiments is to ensure that

Only independent variable changes, everyhting else must be controlled

If these control variables are not kept constant,

can affect results and make them unreliable

A good way to evaluate an experimental design is by

repeating the experiment yourself (using the instructions provided) and determining if you can produce similar results

When analysing and criticising the design of an experiment there are several key things to consider

• Method limitations

• Accuracy

• Precision

• Reliability

• Validity

Method limitation

• A method limitation is any experimental design flaw or fault in the method that affects the accuracy of the results

• must be identiifed and removed

Accuracy

Accuracy is how close a reading/measurement is to its true value

can be reduced by the presence of errors in an experiment

Systematic errors - how to reduce it

systematic errors that are repeated consistently every time the instrument is used or the method is followed - from faulty instruments of flaw in method

instruments should be relicalibrated

Random error

Unexpected environmental changes or incorrect use of equipment can produce random errors 

• are diff each time the experiment occurs

Precision

how similar repeat readings/measurements are to each other

• Readings that are tightly clustered together (a small range) are described as precise

• more decimal places means more precise

Reliability ensured by

repeating experiment

Instruction should have all the required details

Precision vs accuracy

Precision refers to the ability to take multiple readings that are close to each other, whereas accuracy is the closeness of those measurements to the true value.

How to process (occurs before analysis) qualitive and quanatative results

qualitive - observations can be anaylsed (compared to a standard)

quantative - using math skills (statistical tests, work out means and rates, standard devi etc) and presented in graph form

Reduce random error

• Repeat measurements several times and calculate an average from them

Uncertainty

• Uncertainty is the amount of error your measurements might contain, Results will always contain some error so there will always be some uncertainity in readings 

Why is there always uncertainty

because the accuracy and precision of the apparatus being used is limited

margins of error

on glass of apparatus, used to calc percentage error

• The gas syringe may only give readings to the nearest 1 cm³

• The gas syringe has a margin of error of ± 0.05 cm³

• A ‘±’ sign tells you the range in which the true value lies

• The real volume produced could be up to 0.05 cm³ smaller or larger

How to calc percentage error

percentage error = (uncertainty value ÷ your measurement) x 100

Resolution

s the smallest change in the quantity being measured of a measuring instrument that gives a perceptible change in the reading

Smaller measuring instruments have

higher resolution scales due to the smaller graduation so have smaller margin of error

• For example, measuring 5 cm³ of a liquid using a 500 cm³ measuring cylinder would be very difficult. A 10cm³ measuring cylinder would be a more appropriate choice as the measuring scale is of a higher resolution

In an enzyme rate experiment involving the breakdown of hydrogen peroxide by catalase, a student recorded that 10 cm³ of oxygen was produced in 5.245 seconds. The student measured this using a stopwatch that counted in milliseconds. Calculate the percentage error of the stopwatch measurements.

Answer:

Step 1: Calculate the uncertainty value

The stopwatch can measure to the nearest millisecond (0.001 seconds)

This means the actual time taken could be up to 0.0005 seconds shorter or longer than this

This means stopwatch measurements have an uncertainty value of ± 0.0005 s

Step 2: Calculate the percentage error of the student’s measurement of 5.245 seconds

Percentage error = (uncertainty value ÷ your measurement) x 100

Percentage error = (0.0005 ÷ 5.245) x 100

Percentage error = 0.000095 x 100

Percentage error = 0.0095% or 0.01%

SD

• Standard deviation is a measure of the spread or dispersion of data around the mean

Size of SD

• A small standard deviation indicates that the results lie close to the mean (less variation)

• Large standard deviation indicates that the results are more spread out

If there is an overlap between the standard deviations

then it can be said that two sets of results are not significantly different

.69 (+0.02)

0.67-0.71

Using a tangent to find the initial rate of a reaction

bc enzyme reactions make non linear graphs

draw the estimated straight line

Gradient of tangent= change in y divided by change in x 

If the percentage error is too high

any conclusions may be rejected or further testing may be needed to reduce percentage error

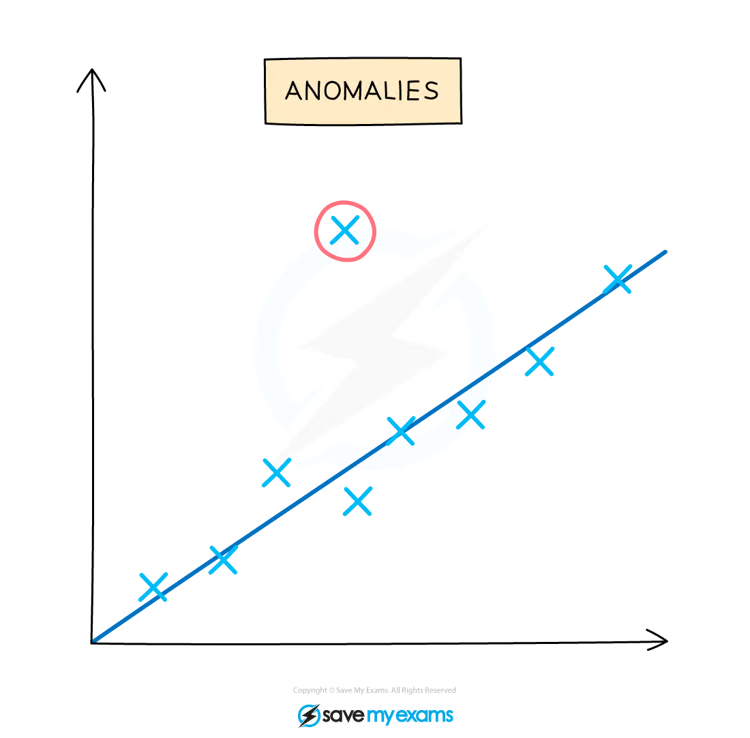
Anomalies

Experimental error will affect results and produce anamolies.

When should anamolies be identified

• These anomalies should be identified during the evaluation of results and before drawing conclusions

How can anamolies be identified

• Anomalies can be identified by looking for results or data points on a graph that don't fit with the trend or with other replicates carried out during the experiment

These anomalous results will show a larger difference from the mean than the rest of the results

ructure for 6-mark planning questions:

• Aim/Hypothesis

• Independent, dependent, control variables

• Step-by-step method (mention repeats + equipment)

• How to measure results

• How to ensure reliability (repeats/means)

• Risk assessment

“Describe how you could investigate the effect of temperature on catalase activity.

• IV: Temperature (°C)

• DV: Volume of oxygen produced (cm³/min)

• CV: pH, enzyme concentration, substrate concentration

• Method: Water bath, gas syringe, repeats

• Safety: Wear goggles (hydrogen peroxide irritant)

Find Sd

find mean, subtract mean from each value, sqaure the values, add them add, then do s= that sqaured divided by n-1

Find uncertanity

+ half the smallest scale divisin

hat a p-value < 0.05 means you  the null hypothesis

reject

Student’s t-test

Compare two means

Chi-squared test (χ²)

Compare observed vs expected frequencies

All types of errors, meaning

Term	Meaning	Example
Accuracy	How close results are to the true value	Using a colorimeter instead of judging by eye
Precision	How close repeated results are to each other	Using apparatus with smaller scale divisions
Reliability	Whether results are consistent and reproducible	Repeating experiment and calculating mean

Reproducibility

Different person or equipment, same trend

percent change formula

((new - original)/original) × 100