CLEP College Mathematics

quadratic formula

-b ± √b² - 4ac / 2a

how to tell if a plot is a function

vertical line test; if it only intersects 1 point, then its a function. if it intersects multiple, then it is not

x/0

undefined

e =

2.71

a^xa^y =

a^x+y

a^xb^x =

(ab)^x

(a^x)^y =

a^xy

a^-x =

1/a^x

a^x / a^y =

a^x-y

(a/b)^x =

a^x / b^x

y = log_a(x) =

a^y = x

log_a(xy) =

log_a(x) + log_a(y)

log_a(x/y) =

log_a(x) - log_a(y)

log_a(x^y) =

y log_a(x)

log_a(1) =

0

log_a(a) =

1

log_a(0) =

undefined

domain

what x can be, from a starting number to an end number

range of a function

is what f(x) can be, from a starting number to an end number

√-x =

undefined

“( )” meaning

• endpoint is not included in set

• infinity signs (-∞,∞) always use parentheses

• represented with an OPEN dot

“[ ]” meaning

• endpoint is included in set

• represented with a CLOSED dot

(x, ∞) =

all numbers greater than x

(-∞, x) =

all numbers less than x

(-∞,∞) =

all real numbers

f(x) → f(x + a)

shifts the function to the left by a

f(x) → f(x - a)

shifts the function to the right by a

f(x) → f(x) + b

shifts the function up by b

f(x) → f(x) - b

shifts the function down by b

f(x) → f(-x)

reflects the function over the y axis; left/right

f(x) → -f(x)

reflects the function over the x axis; up/down

f(x) → -f(-x)

reflects the function on both the x and y axis

how to know if a function is even

when f(x) = f(-x)

how to know if a function is odd

when f(-x) = -f(x)

how to tell if a plot is a inverse function

the horizontal line test; if it only intersects 1 point, then its a inverse function. if it intersects multiple, then it is not

how do you find an inverse of a function

switch x and y, then solve for y

• f(x) = x → y = x

linear function formula

y = mx + b

• ex; a library has 8,000 books and is adding 500 more books each year

  • 500x + 8,000

exponential function

f(x) = a^x · b

• ex; a bank account starts with $10, every month, the amount gets tripled

  • 3^x · 10

given n, how many groups of k possible, if order doesn’t matter

(n / k) = n! / k! (n-k)!

• “choose”

• “combinations”

• “group”

• “set up”

given n, how many groups of k possible, if order does matter

n! / (n-k)!

• “arrange”

• “permutation”

• “line up”

• “sequence”

how many combinations can you make with 1 appetizer (a options), 1 main dish (b options), and 1 dessert (c options)

multiply a × b × c

4!

4 × 3 × 2 × 1 = 24

all probabilities have a value from

0-1

A ∪ B

The union of A and B; the event that either A or B occurs

A ∩ B

The intersection of A and B; the event that both A and B occur

A^c

The complement of A; the event that A does not occur

A / B

The difference between sets; the set of elements that are in A, but not B

P (A ∪ B) =

P(A) + P(B) - P(A ∩ B)

P(A ∩ B) =

P(A) · P(B)

in probability, the events A and B are independent if

what happens to A doesn’t affect B and vice versa

P(A|B)

The conditional probability of A on B; given the information about event B, what’s the probability of A occurring

P(A|B) =

P(A ∩ B) / P(B)

P(A^c) =

1 - P(A)

mean

the average; add all data, divide by the amount of data

median

the middle point; sort data, and find middle number. if theres an even number of data points, find the mean of the 2 middle numbers

mode

the number that appears most often

range

the largest value - the smallest value

Inner quartile range

median of the 75th percentile (2nd half) - median of the 25th percentile (1st half); find the median of the entire set, then find the median of the 2 halves

Variance of data

1/n (x_k - m)²

• how much the values in a dataset deviate from the average

• n = number of data points, x_k = data point, m = mean

Standard deviation of data

√1/n (x_k - m)² (square root of variance)

• how dispersed the data is in relation to the mean

Normal distribution

a probability distribution that appears as a "bell curve" when graphed

low standard deviation

most of the points are very close to the mean; thin tails; cluster / high concentration

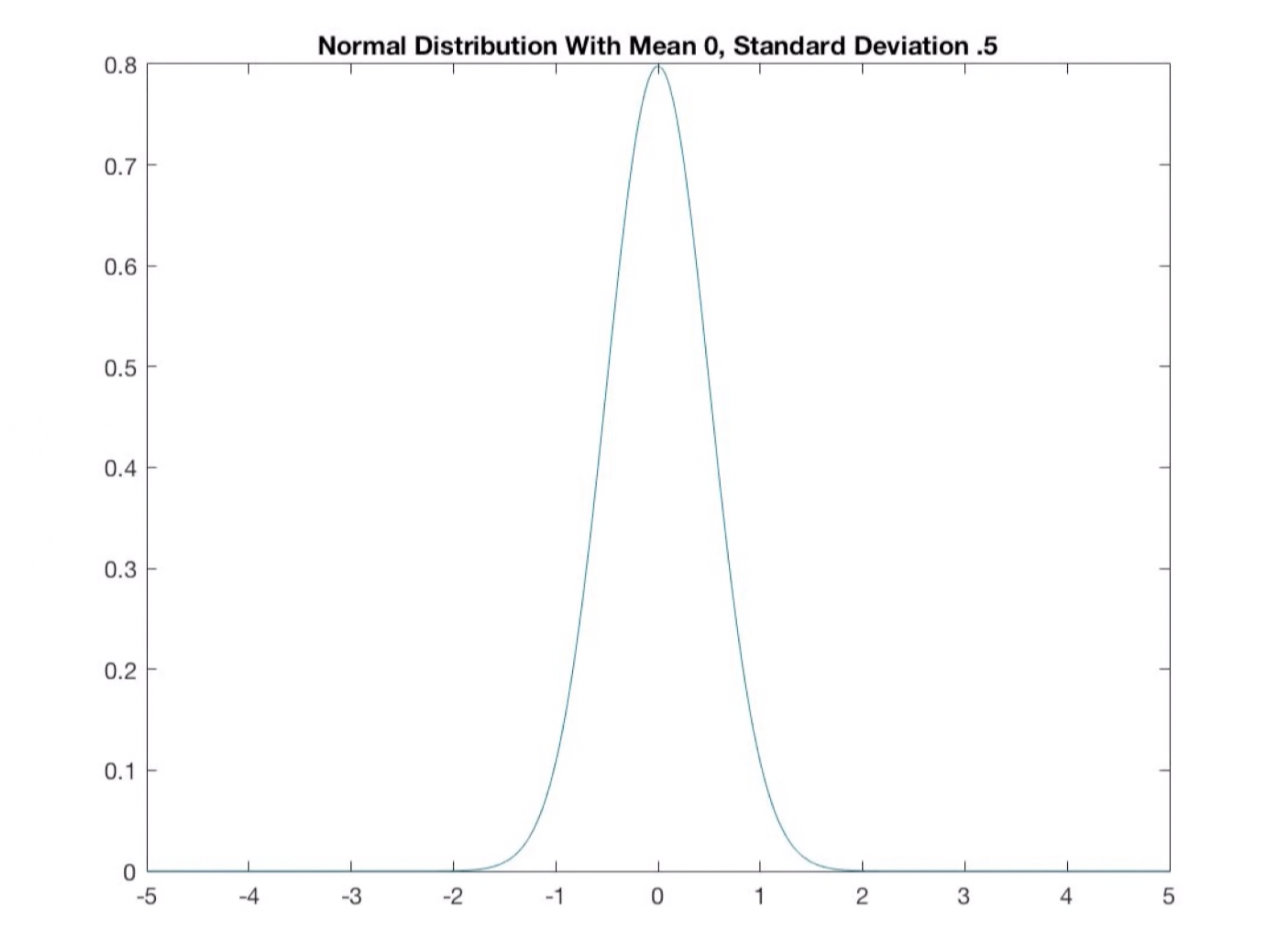
low standard deviation

high standard deviation

most of the points are spread out relative to the mean; fat tails; diffused / low concentration

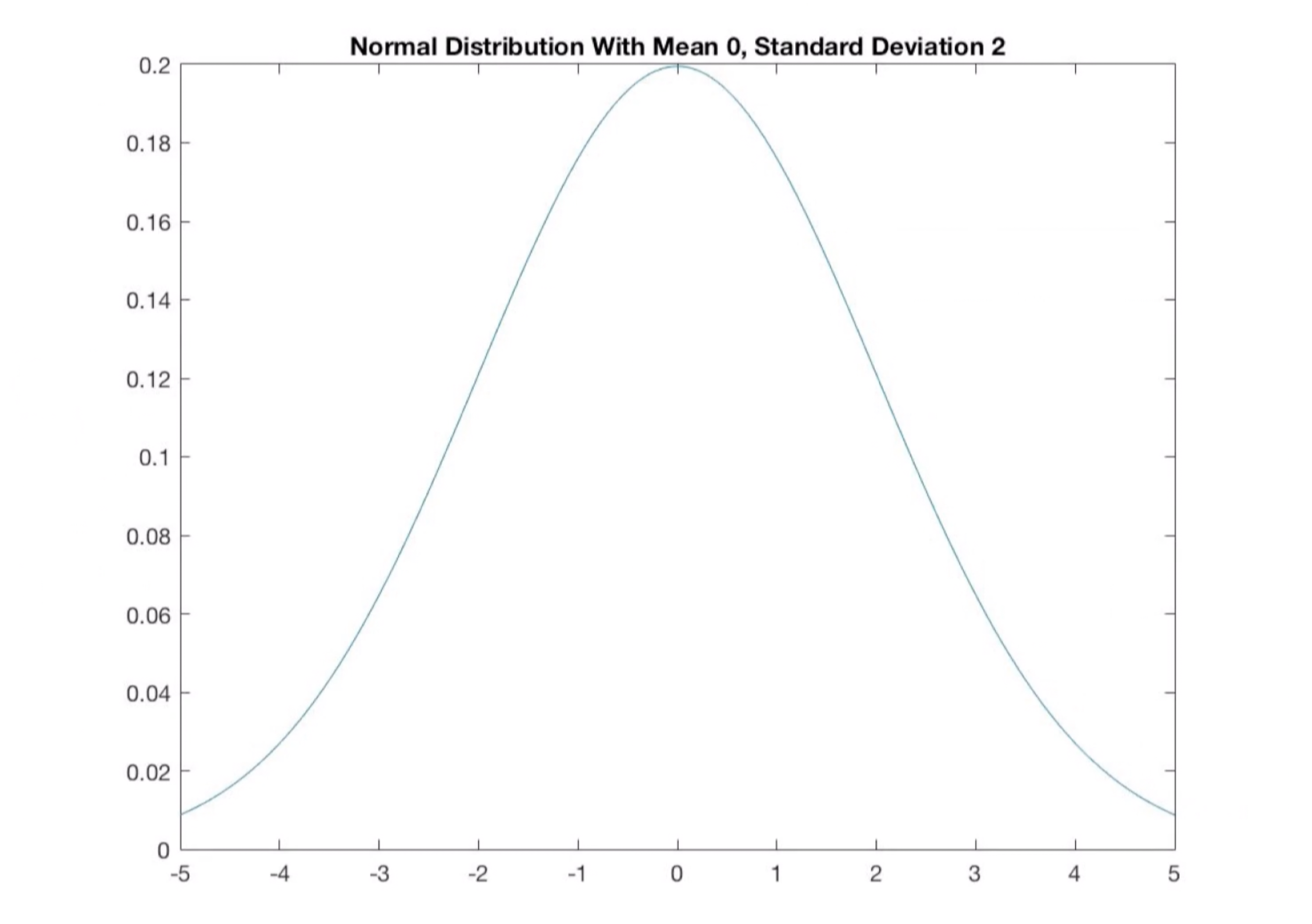
high standard deviation

Positive regression line slope

(line goes up) - positive correlation between the two variables; if one variable increases, the other will also increase

Negative regression line slope

(line goes down) - negative correlation between the two variables; if one variable increases, the other will decrease

Nonlinear association line slope

Unable to draw a line through the data; usually a curve

No association line slope

No clear pattern

effective rate

tax paid / principal amount

• the actual percentage of income that an individual or corporation pays in taxes

Relative Mark up/down

Total Mark up/down / Original Price

• the increase/decrease in price of a product or service compared to its original cost or cost of goods sold

simple interest

I = P x R x T

• I = interest, P = principal amount, R = rate of interest, T = time

Compound Interest

A = P (1 + r/n)^nt

• n = compounding rate; how many times the interest on the interest is collected

  • ex; yearly, n = 1. daily, n = 365, quarterly, n = 1

Compounding continuously

A = Pe^rt

Effective Annual Yield

EAY = (1 + r/n)ⁿ - 1

Parallel lines

lines that never intersect

how to know if 2 lines (y = m₁ + b₁, and y = m₂ + b₂) are parallel

if m₁ = m₂

Perpendicular lines

lines that intersect at a 90° angle

how to know if 2 lines (y = m₁ + b₁, and y = m₂ + b₂) are perpendicular

if m₁ = -1/m₂

perimeter of a triangle

a + b + c

area of a triangle

½ bh

angles of a triangle sum up to

180°

Equilateral triangle

triangle with equal length on all sides; same angles of 60°

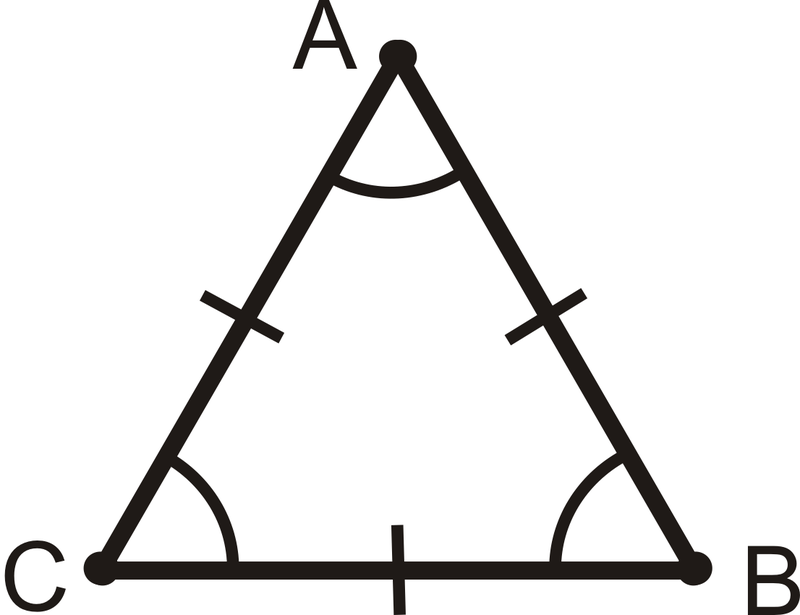
equilateral triangle

Isosceles triangle

triangle with equal length on 2 sides; 2 of the same angles

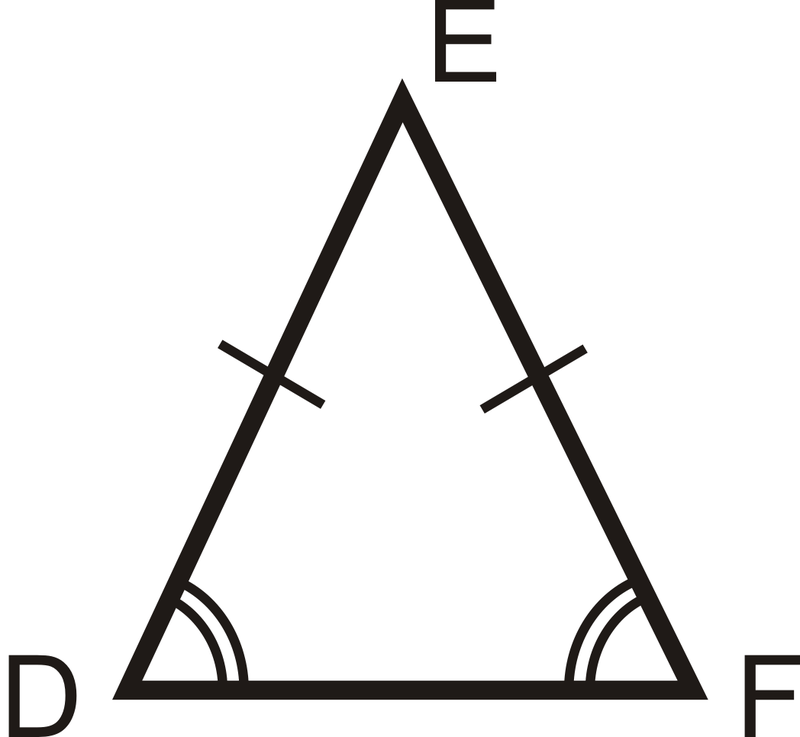
Isosceles triangle

Scalene triangle

triangle with all different lengths; all different angles

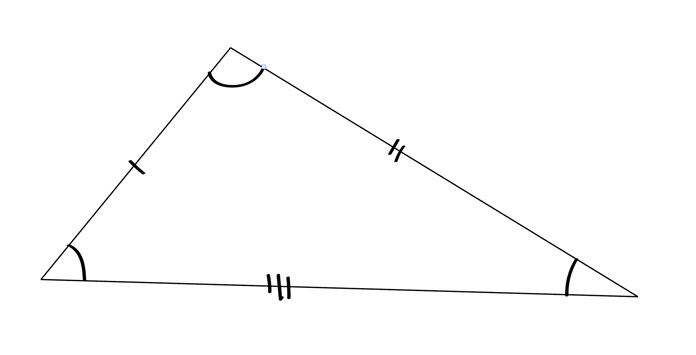
Scalene triangle

pythagorean theorem

a² + b² = c²

Parallelograms

quadrilaterals with opposite sides parallel

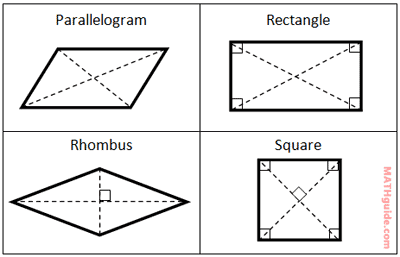
area of a parallelogram

Area = BH

Trapezoids

quadrilaterals with one pair of opposite sides parallel

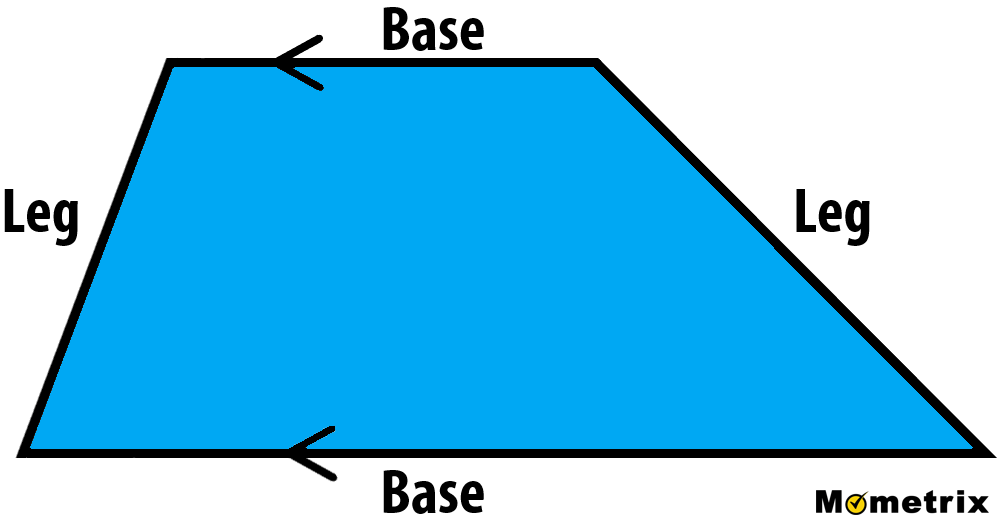
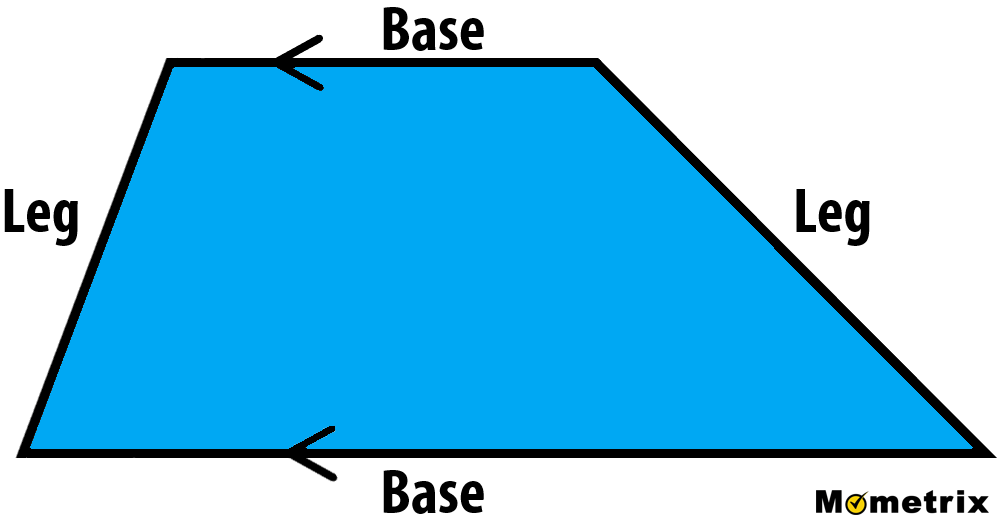
Trapezoid

area of a trapezoid

Area = (B₁ + B₂ / 2) x H

Radius

R = D/2

• distance from the center

area of a circle

Area = πr²

π =

3.14

Circumference

C = 2πr

• “length” of the circle (perimeter)

Diameter

D = 2r

• the distance of a line going across the circle through the center

To find the area of one piece of a circle

Area of arc = 𝚹​ / 360° x πr²