1) From Clouds to disks

How are the stars and planetary system around them are formed?

They are formed by a local contraction of Giant Molecular Clouds (GMCs) in the Interstellar Medium (ISM).

What is an InterStellar Medium (ISM)?

is the matter and radiation that exists in the space between the star systems in a galaxy. This matter includes gas in ionic, atomic, and molecular form, as well as dust and cosmic rays.

Where would the molecular clouds preferably form?

in the spiral arms of the Milky Way

What are typical characteristics of GMCs?

Mass about 10^4 to 10^6 time mass of the sun, distant are about 10-100pc (parsec), the number of molecules per volume are about thousands to millions per cubic centimeter, and the temperature is about 20 Kelvin. Composition is 99% molecular gas like hydrogen, helium or CO (carbon monoxide) and the rest of 1% are dust (mostly silicates which are less then 1 micrometers)

Nearby well-studied GMCS:

- Taurus (distance 140 pc, size 30 pc, mass 10* Mo) quiet slow star formation, mostly isolated low-mass stars - Orion [Orion nebula is part of it] (distance 400 pc, size 60 pc, mass 106 Mo) intensive star formation, many luminous O-stars - others: Ophiuchus, Chamaeleon, Serpens...

Jeans criterion

the criterion for the cloud collapse! The cloud will be gravitationally unstable, and will start to contract if the potential energy of the gravitational field U exceeds the kinetic energy of the thermal motion of the molecules K: K<U or v^2<GM/R

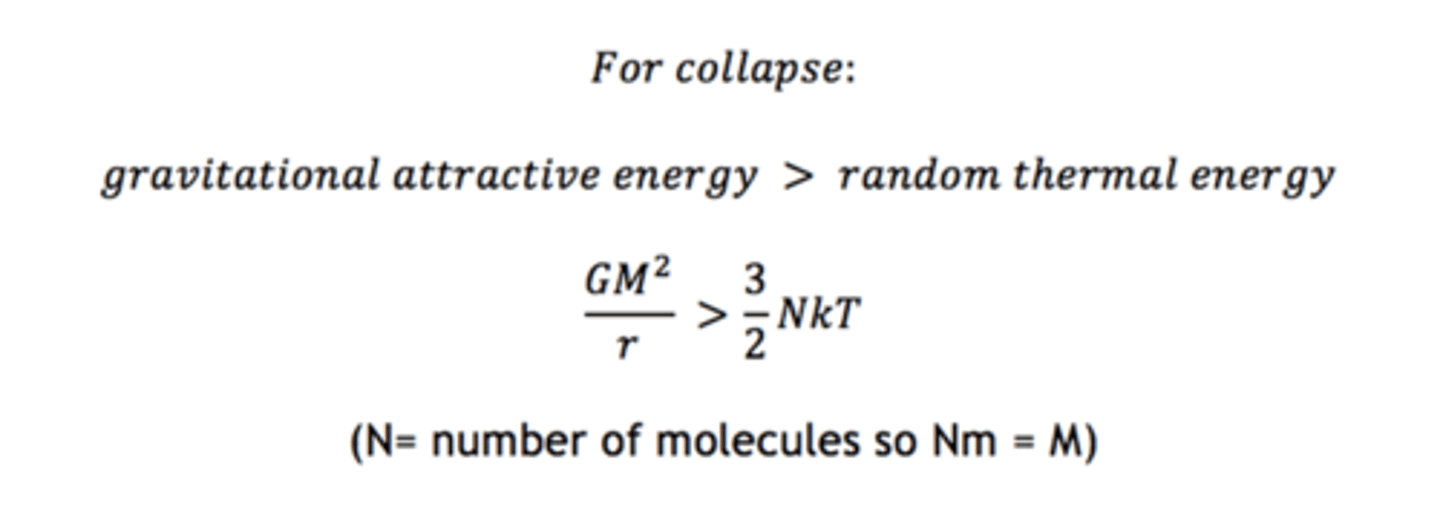
When will the cloud start to collapse?

When the inequality fulfill where constant k time Temperature diving by protons mass (hydrogens molecules) is smaller than Gravitational acceleration time mass dividend by radius.

Jeans radius

Or critical radius can be found if we know mass of the cloud and if the mass cloud is smaller than this Jean radius it will start to contract so R less than proton mass multiply by gravitational constant and mass of the cloud divide by constant k time temperature.

Jeans Mass

The mass of an interstellar gas cloud that is just unable to support itself against its own gravity
So it will collapse

The mass of the most molecular cloud is much larger than Jeans' mass so why don't they all immediately start to collapse?

Because there are other physical effects that we didn't take into account and some are stabilizing factors that prevent the cloud from contracting like magnetic field, rotation.

And other help the cloud to collapse like

The Jeans mass for a cloud is much larger that the mass of a typical star or a typical planetary system; why aren't stars that massive?

Because the collapsing cloud fragments, and those fragments yield numerous stars.

Evolution of a cloud goes in two major steps

First, a filamentary structure develops. This process is essentially driven by magnetic field rather than gravity.

Second, each filament, if Jeans-overcritical, starts to collapse. What is even more important,the filament does not stay homogeneous: it will "split" into smaller subclouds (fragmentation).

Angular Momentum problem

the Sun in our model rotates too fast, while the planets move too slowly??

Which means ---> the planets have gotten the angular momentum, from the Sun which,therefore must have slowed down somehow!

Possible solution for Angular Momentum Problem

1) the young star can get rid of the extra angular momentum through the magnetic coupling via the stellar wind into the ISM, or

2)the angular momentum transport outwards may exist through the viscosity of the disk

How is star embryos or 'COREs' are formed

a fragment of a molecular cloud with the stellar mass, contracts from Core Radius to Disk Radius and, in doing so, also flattens, spins up and heats up

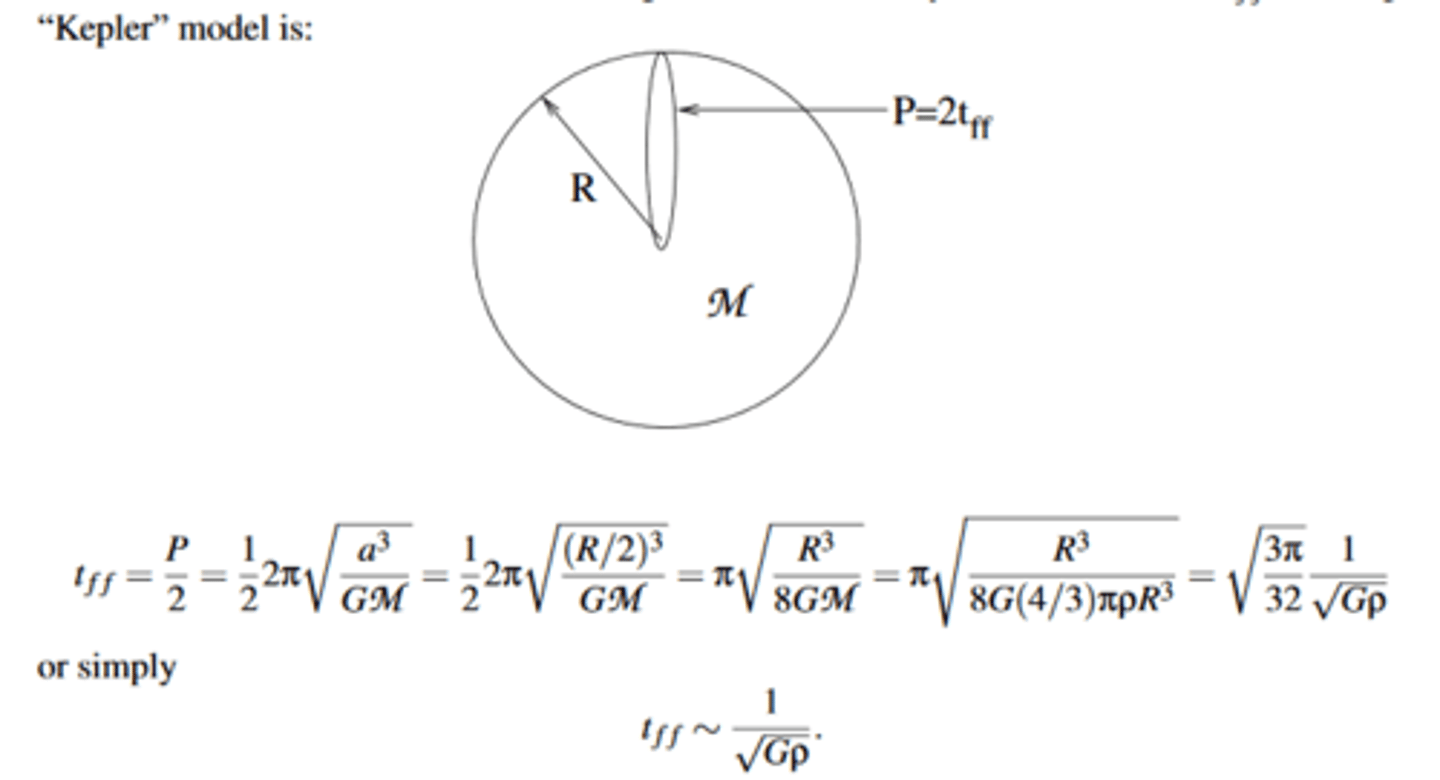
Contraction time

or flattening time is essentially the free-fall time, t ff

t ff is about 1 over square root of Gravitational constant time density rho

Interestingly, t ff is almost independent of the mass or radius, only on the (mean) density of the matter.

estimates lead to timescales, about ⇠ 10^4 years

(how long doesit typically take before the protostar forms in the center, surrounded by a protoplanetary disk?)

Thermal Time

or the Helmholtz-Kelvin time t HK, is defined as the time interval over which a star can sustain its luminosity by the gravitational energy:

For the "present-day Sun", we obtain about 30 million years

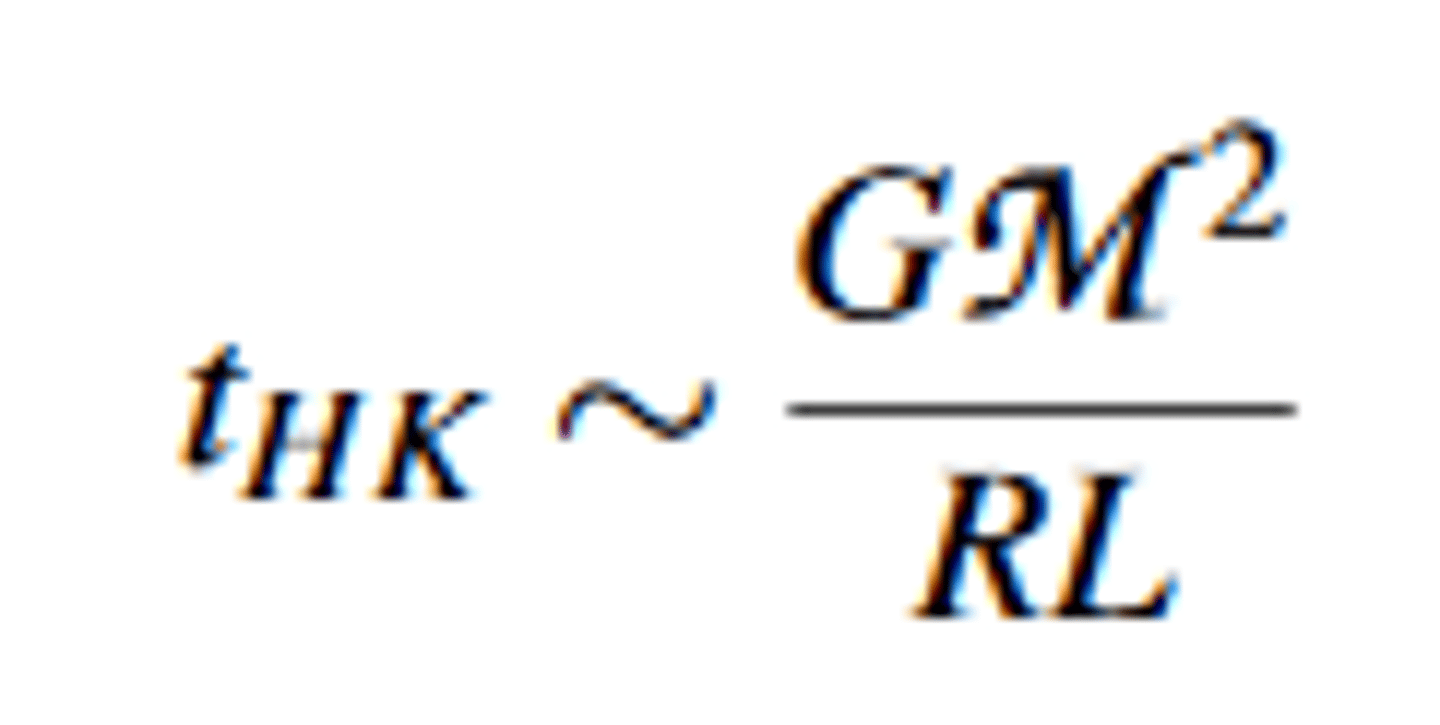
Nuclear time

t nuc. is defined as the time interval over which a star can sustain its luminosity by the nuclear fusion

0.01 —because about 1% of the rest energy goes to radiation in the p-p cycle — the mass ofan alpha-particle is by 1% less than four times the proton's mass

For the "present-day Sun": nuclear time is about 10^10 years

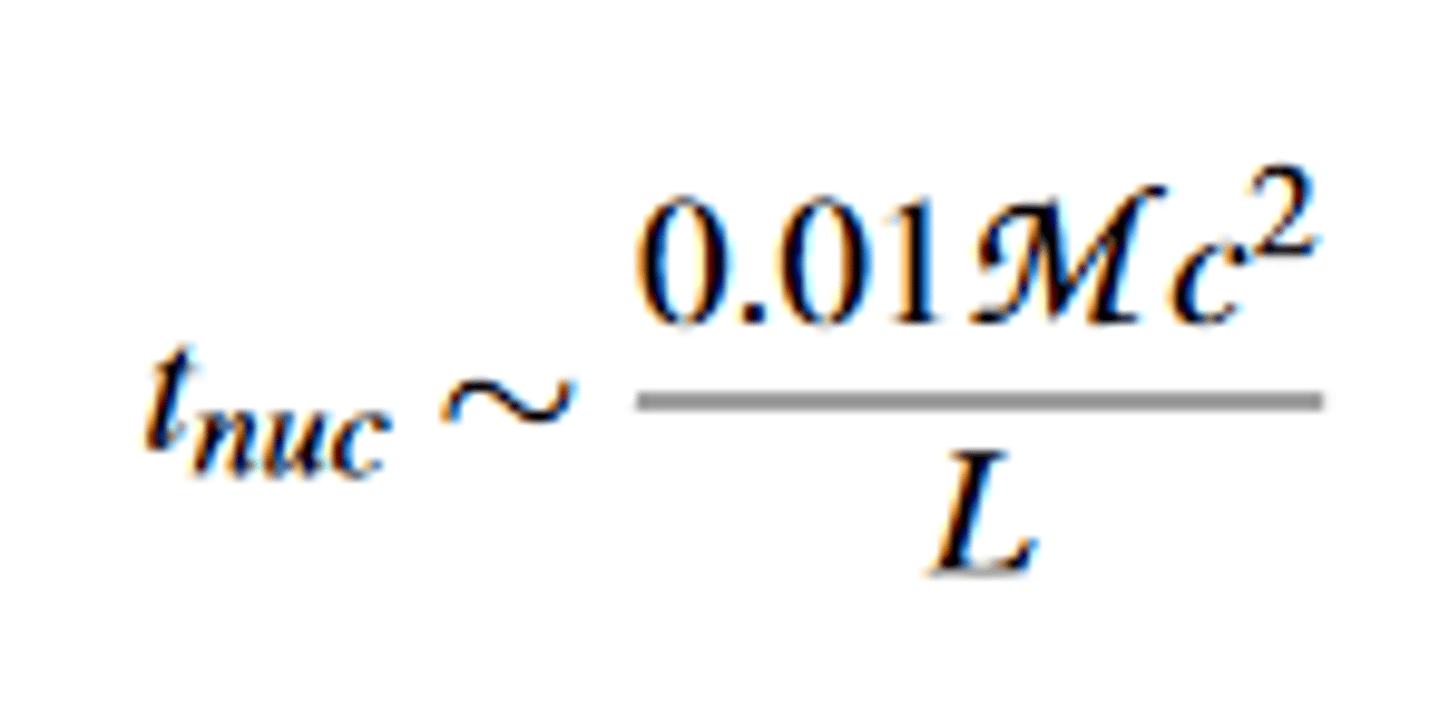
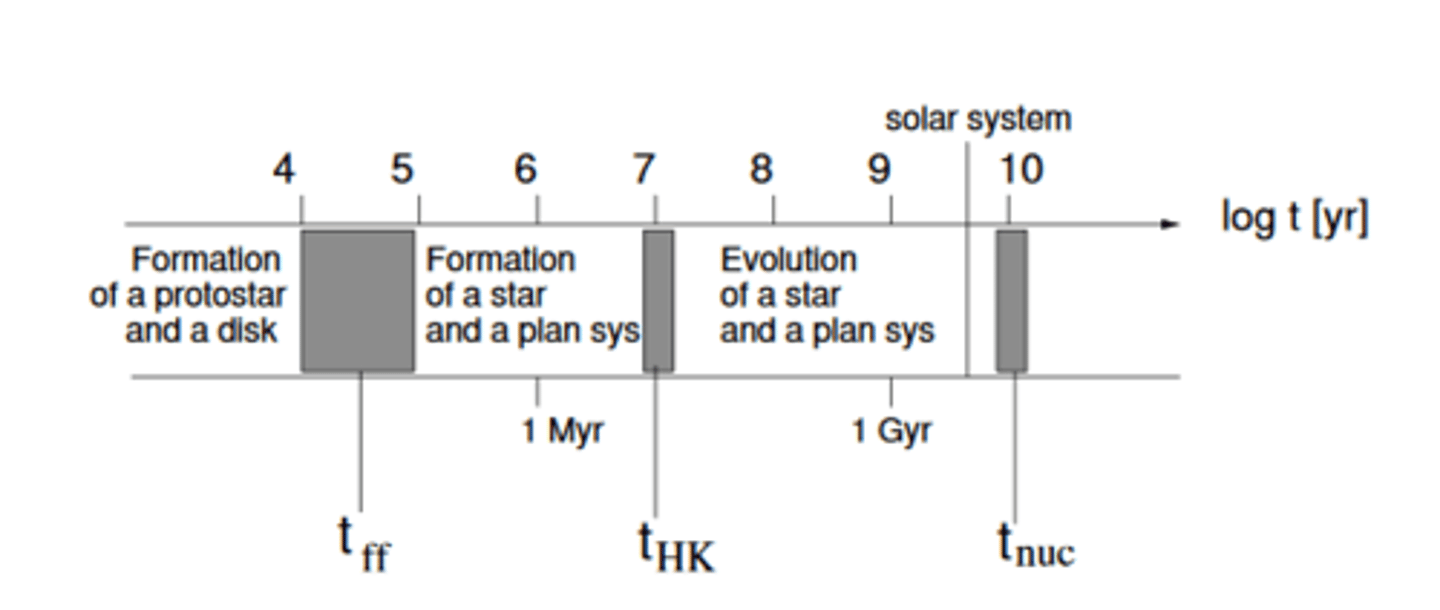
Orient ourselves in time:

1) After a cloud of stellar mass starts collapsing, the protostar should emerge in⇠10^4-10^5 year. We expect it to be surrounded by circumstellar material, namely in form of a protoplanetary disk, from which a planetary system would form.

2) Whatever the processes in the protostellar disk, it can be strongly influenced by processesin the protostar itself, especially on timescales of⇠10^7 year when the fusion begins. (But: the disk has its own timescales, which we don't know yet!)

3) A planetary system, if emerged, has⇠10^10 year to evolve (for solar-type stars), before the star goes into a red giant phase