CIRCULAR MOTION TO REMEMBER

Uniform circular motion

An object rotating at a steady rate (constant speed) moves in uniform circular motion.

Angular displacement, θ

Angle in radians of the object's displacement after a time t. θ = 2πft

Angular speed, ⍵

Angular displacement per second. ⍵ = 2πf

Linear velocity

The velocity of the object at one instant. Directed along the tangent of the circle i.e. at right angles to the centripetal force

Centripetal acceleration

Change in the direction of the velocity per second. The centripetal acceleration is directed towards the centre of the circle. a = v²/r = r⍵²

Centripetal force

Resultant force on an object moving in uniform circular motion, directed towards the centre of the circle. F = mv²/r = mr⍵²

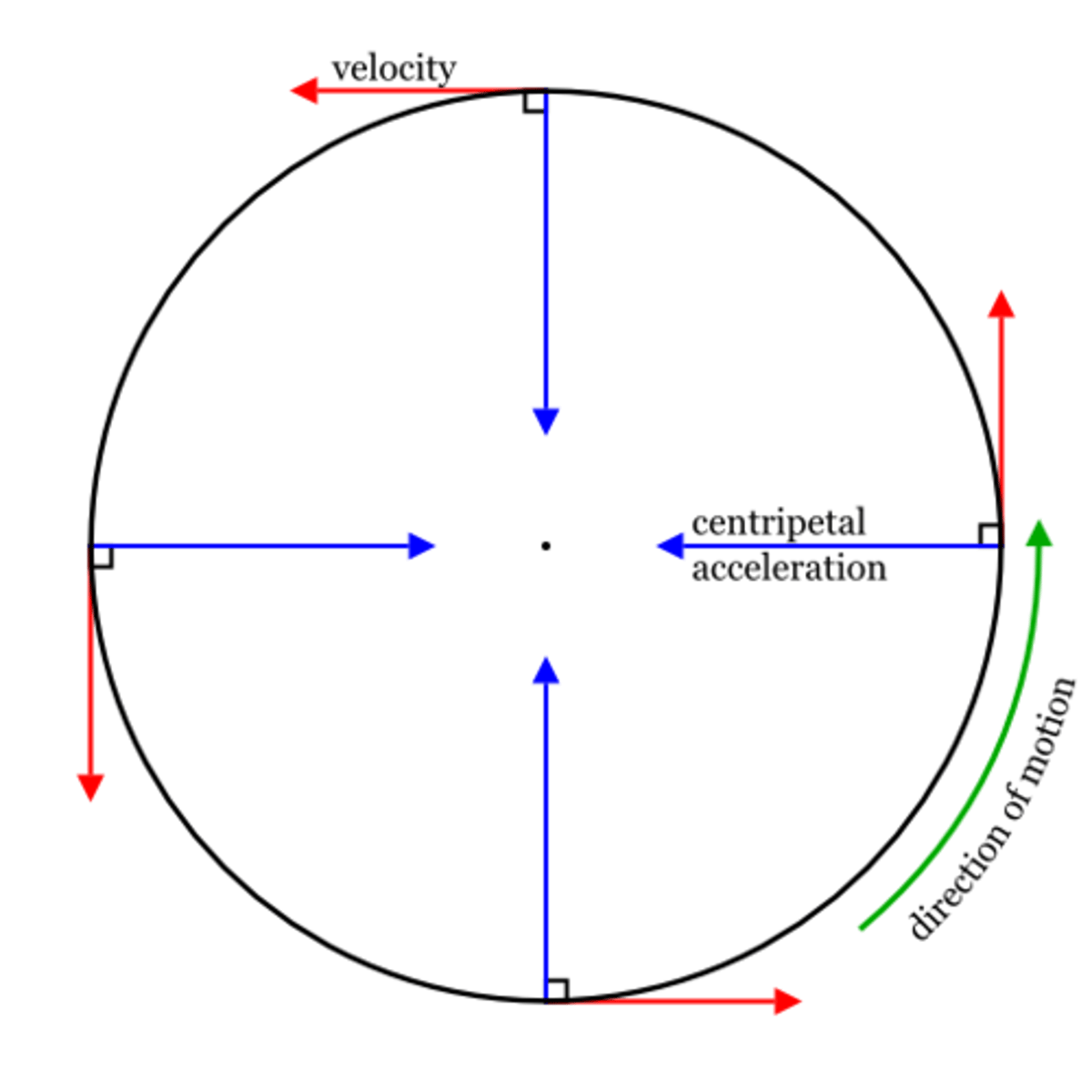
What are the directions of centripetal acceleration, centripetal force, velocity & direction of motion

Acceleration & Force = same direction, towards the centre of the circle

Velocity is perpendicular to the direction of the force

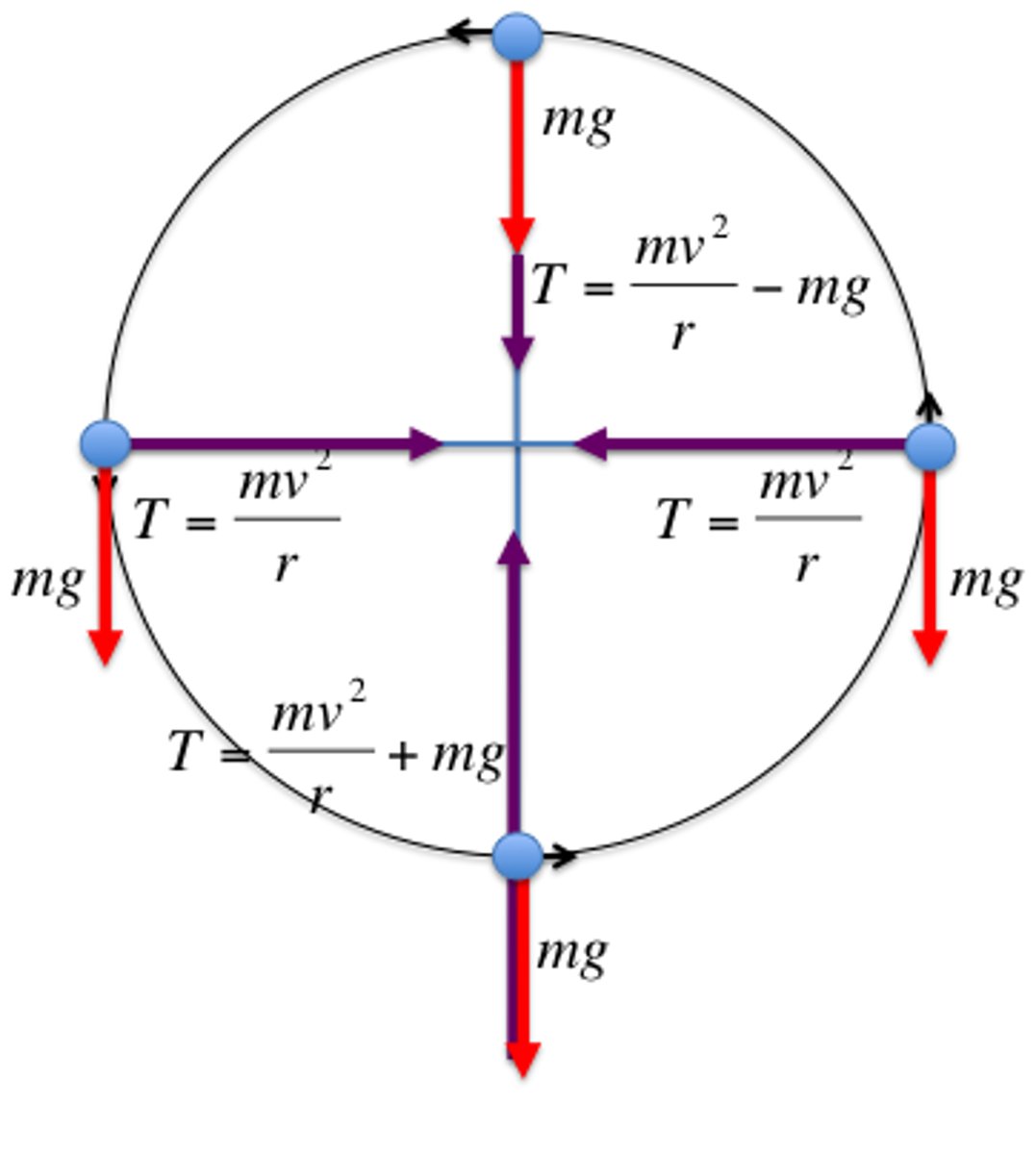
Vertical circle

Bottom has the highest tension

Top has the lowest tension

Horizontal circle

R = mg

Centripetal F = mv²/r

∴ v ∝ radius of the road

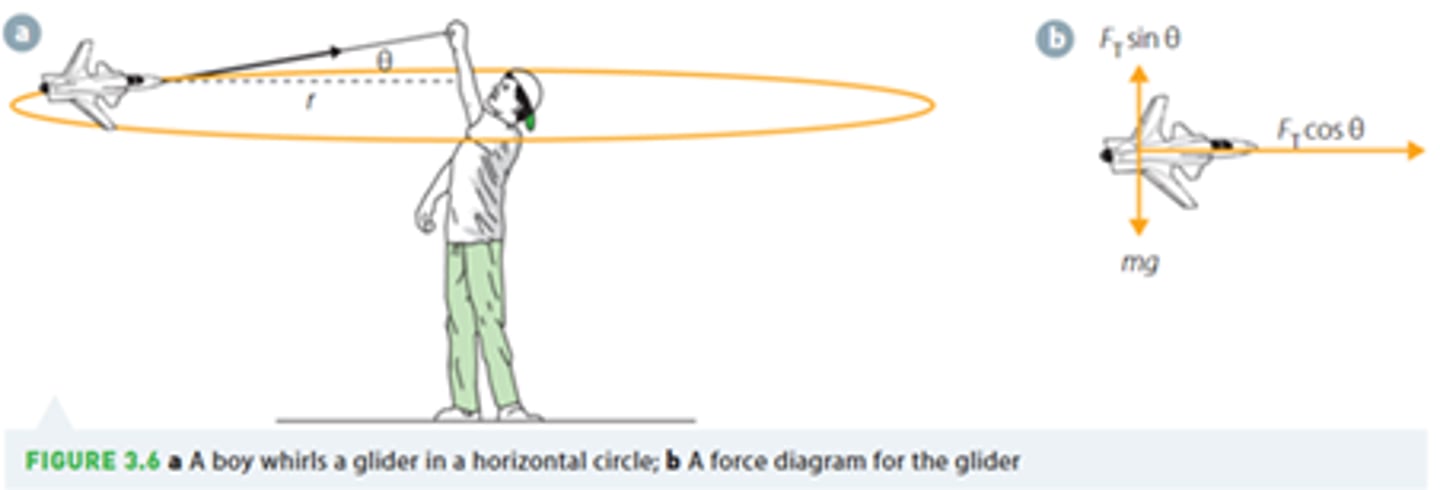
Banked road

Rcosθ = mg (1)

Rsinθ = mv²/r (2)

(2)/(1) → tanθ = v²/rg

∴ v² ∝ θ

Revolutions per minute → Radians per second

(𝔁 x 2π) / 60 = rad s⁻¹

Radians per second → Revolutions per minute

(𝔁 x 60) / 2π = rev min⁻¹

Equation linking θ, ⍵, t

θ=⍵t