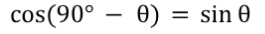BC Pre Calc Final

Formulas, transformations, identities

Even Function (graphic)

symmetric over y-axis

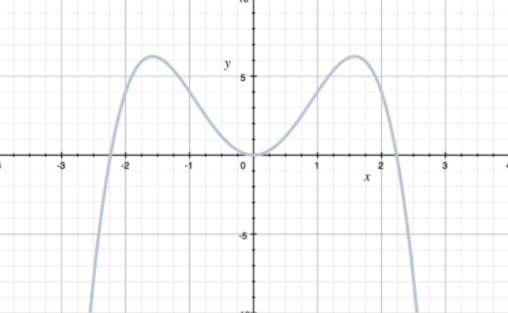
Odd Function (graphic)

symmetric about the origin

Even Function (algebraic)

f(–x)=f(x)

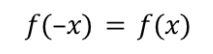
Odd Function (algebraic)

f(–x)=–f(x)

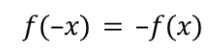
y=x

linear parent function

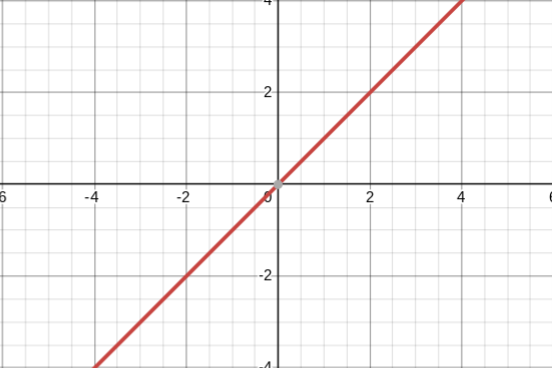
y=x²

parabola parent function

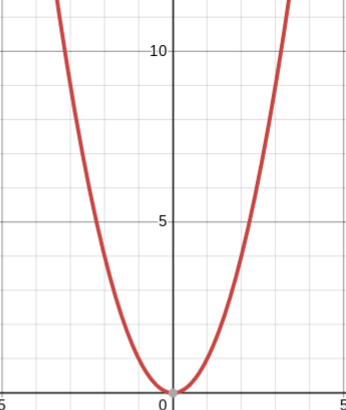
y=x³

cubic parent function

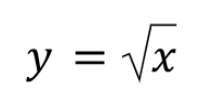
square root parent function

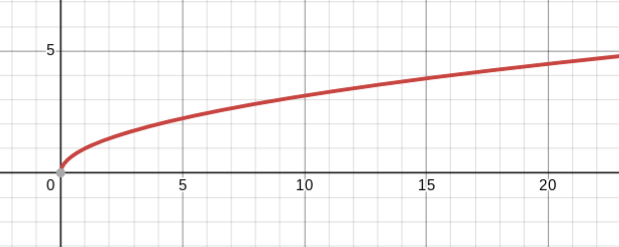
y=|x|

absolute value parent function

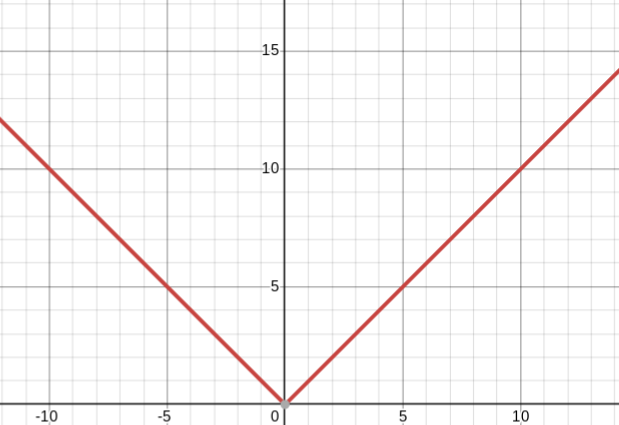
y=e^x

natural exponential parent function

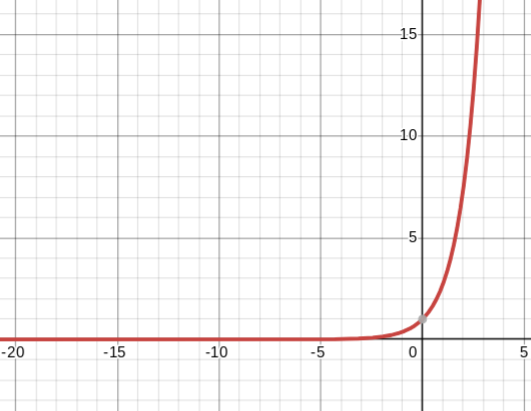
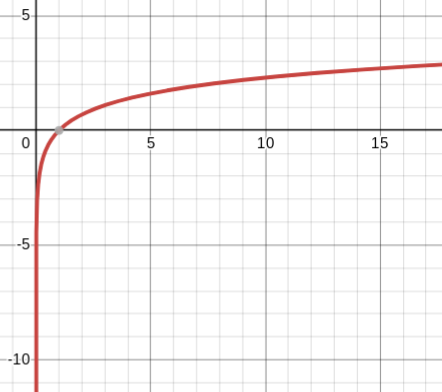
y=ln x 

natural log parent function

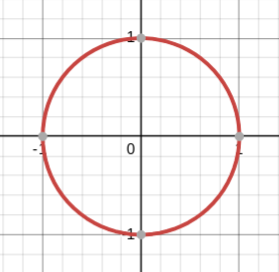
x²+y²=1

unit circle (circle parent function)

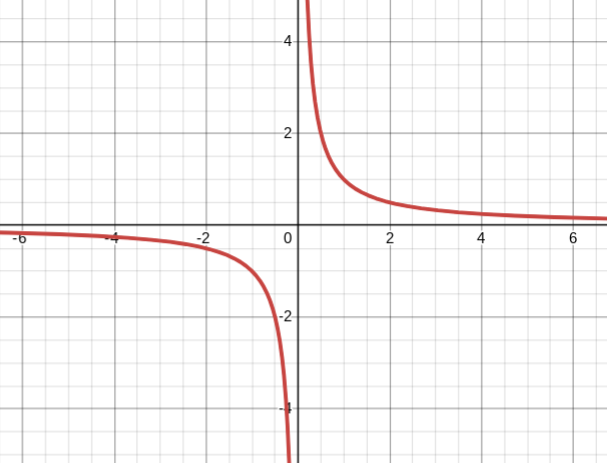
y=1/x

reciprocal parent function

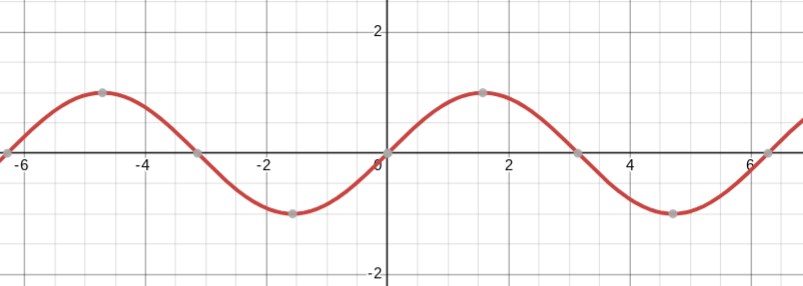
y=sin(x)

sine parent function

y=cos(x)

cosine parent function

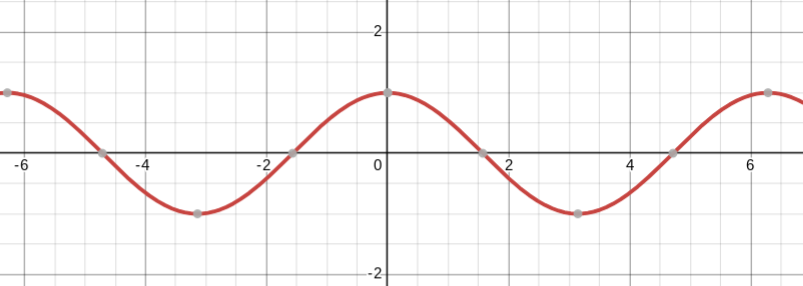
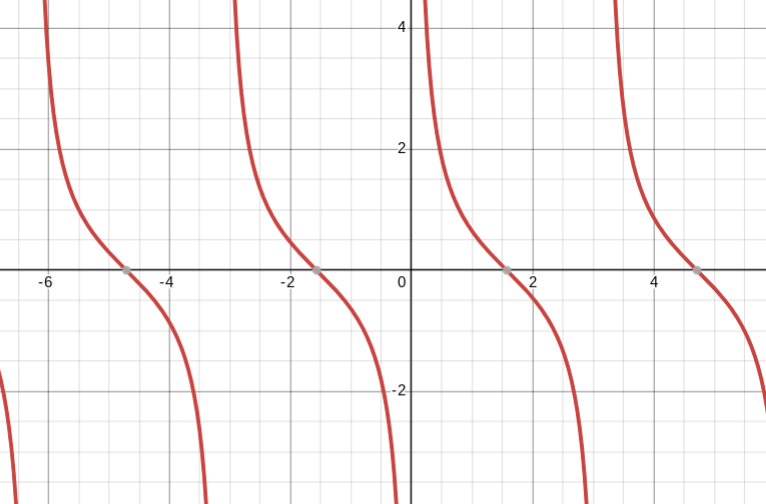
y=tan(x)

tangent parent function

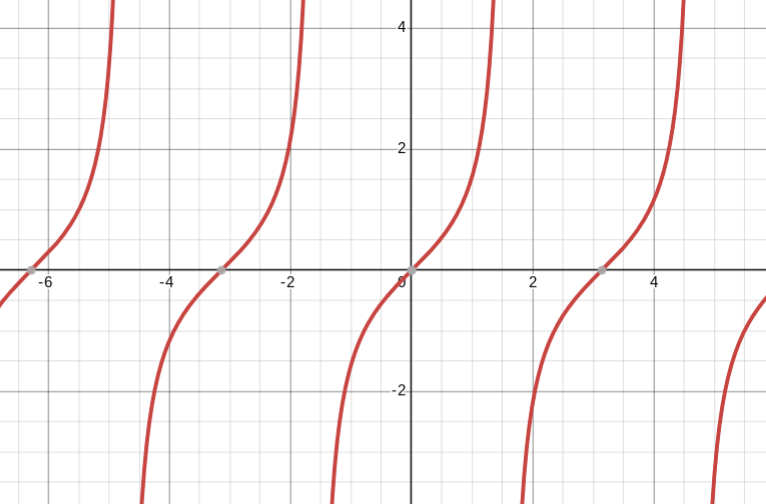
y=csc(x)

cosecant parent function

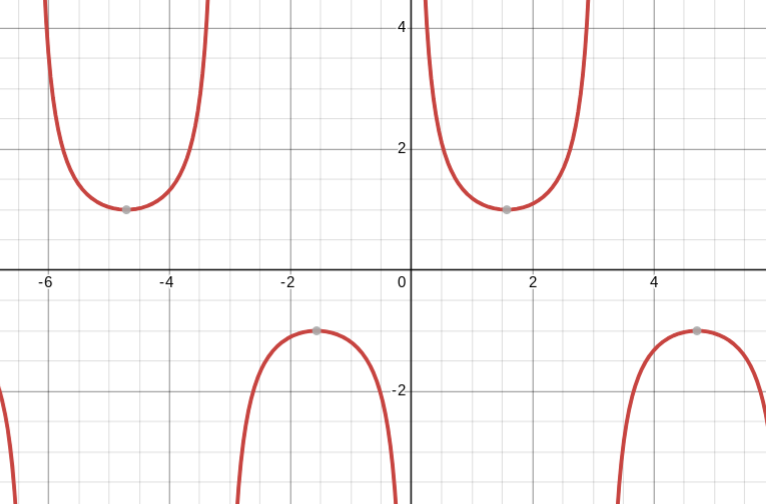
y=sec(x)

secant parent function

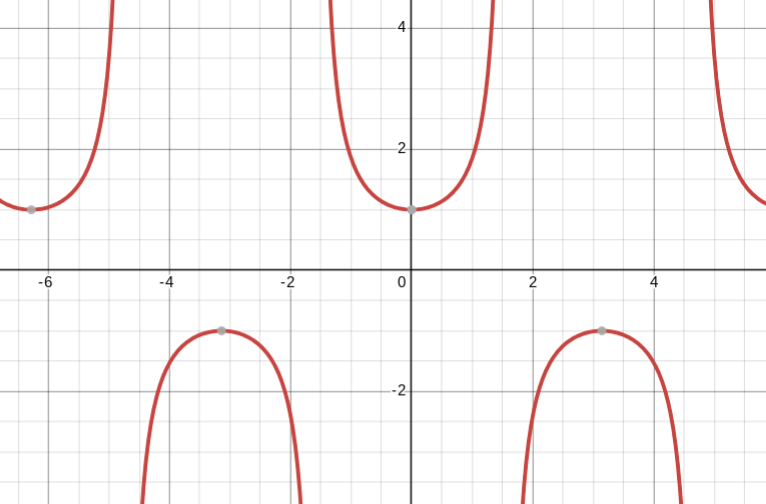
y=cot(x)

cotangent parent function

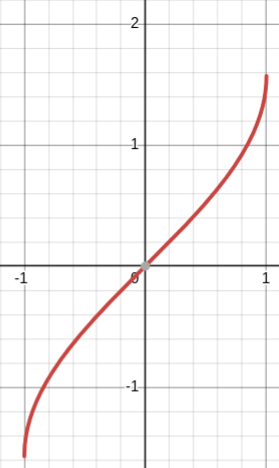
y=sin^-1(x)

inverse sine parent function

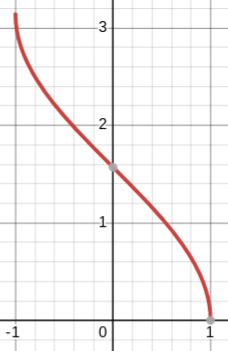
y=cos^-1(x)

inverse cosine parent function

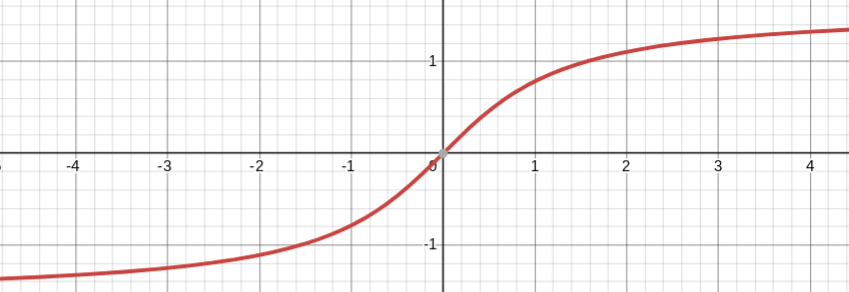
y=tan^-1(x)

inverse tangent parent function

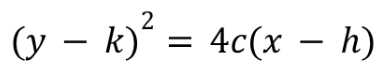
(y-k)²=4c(x-h)

horizontal parabola equation

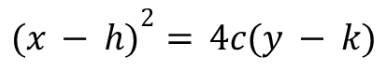
(x-h)²=4c(y-k)

vertical parabola equation

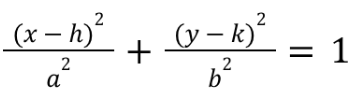
horizontal ellipse equation

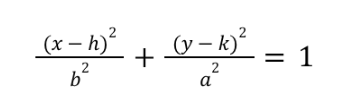
vertical ellipse equation

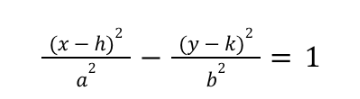
horizontal hyperbola equation

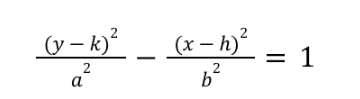
vertical hyperbola equation

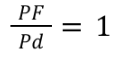
parabola eccentricity

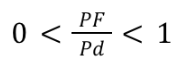
ellipse eccentricity

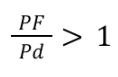
hyperbola eccentricity

parabola: (h, k)

vertex

parabola: c

direct distance between vertex and focus

ellipse: (h, k)

center

ellipse: b²+c²=a²

distance from the center to a focus

ellipse: 2a

length of major axis

ellipse: 2b

length of minor axis

ellipse: 2c

distance between foci

hyperbola: (h, k)

center

hyperbola: b²+a²=c²

foci relationship

hyperbola: c

distance from center to focus

hyperbola: a

distance from center to vertex

hyperbola: b

distance from center to co-vertex

hyperbola: 2a

length of major axis

hyperbola: 2b

length of minor axis

hyperbola: 2c

distance between foci

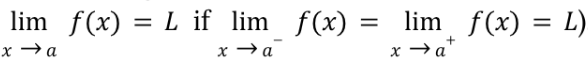
limit of a function exists

Intermediate Value Theorem (IVT)

 If f(x) is continuous on [a, b] then for every y between f(a) and f(b) there exists an x = c between a and b such that f(c) = y

Continuity (basic)

a graph can be drawn without needing to lift the pencil

Continuity (calculus)

 for a function f to be continuous at the point x = c, then all three conditions below must be met

Three conditions for continuity

f(c) exists

the limit of f(x) as x approaches c exists

the limit of f(x) as x approaches c equals f(c)

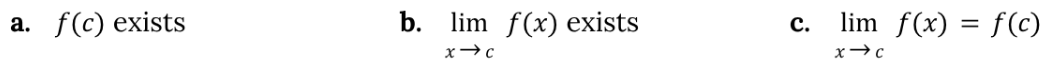
Remainder Theorem

if a polynomial function, f, is divided by (x - a), then the remainder is f(a)

Factor Theorem

if (x - a) divides a polynomial function, f, evenly, then f(a) = 0

Slope of a Secant Line

the slope to f(x) on [a, b] is (f(b) - f(a)) / (b - a)

Slope of a Tangent Line

the slope to f(x) at x = c is the derivative and is f'(c)= the limit of (f(x) - f(c)) / (x - c) as x approaches c

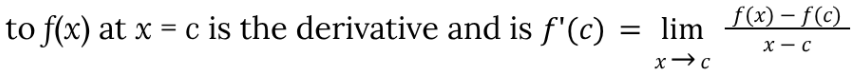
Point-Slope Form

(y-y₁) = m(x-x₁)

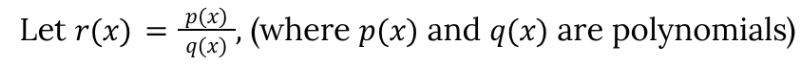
Rational Functions Graph Properties: zeros

r(x) will have zeros where p(x) = 0

Rational Functions Graph Properties: vertical asymptotes

r(x) will have vertical asymptotes (infinite discontinuities) for all zeros of the denominator with greater multiplicities than there are zeros of the numerator

Rational Functions Graph Properties: holes

r(x) will have holes (removable discontinuities) for all zeros of the numerator with equal or greater multiplicities than there are zeros of the denominator

Rational Functions Graph Properties: horizontal asymptotes

• y=0 when the degree of q > the degree of p

• y=a/b when the degree of q = the degree of p

  • (where a = leading coefficient of p and b = leading coefficient of q)

• r(x) will have a slant asymptote when the degree of q < the degree of p

  • Equation of slant asymptote can be found by dividing p and q

Inverse of logarithmic function

exponential function (and vice versa)

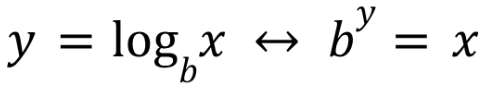
definition of e¹

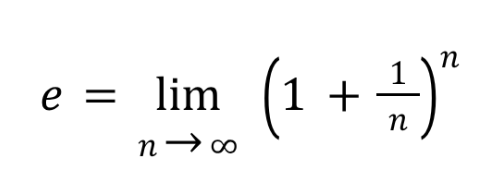
definition of e^x

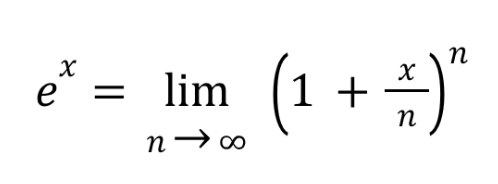
Compound interest (n times per year)

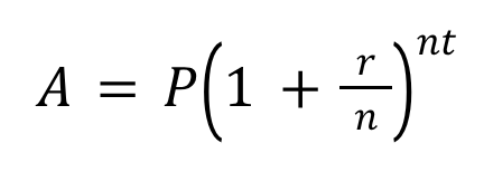
Compound interest (continuously)

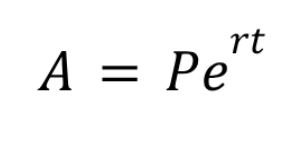
Log Property (1)

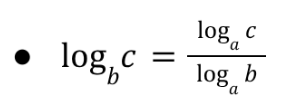
Log Property (2)

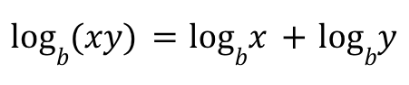
Log Property (3)

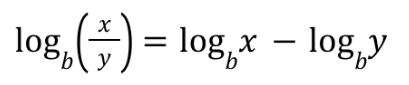
Log Property (4)

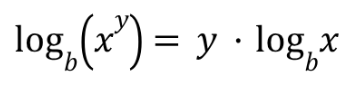
Unit Circle: sine ratio

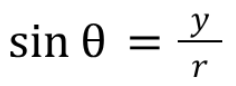
Unit Circle: cosine ratio

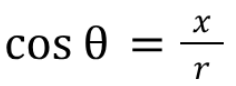
Unit Circle: tangent ratio

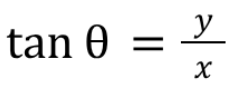
Trig Functions: y=sin(x) domain

(negative infinity, infinity)

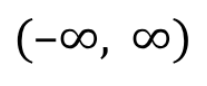
Trig Functions: y=sin(x) range

[-1, 1]

Trig Functions: y=cos(x) domain

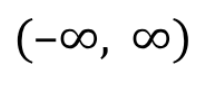
Trig Functions: y=cos(x) range

[-1, 1]

Trig Functions: y=tan(x) domain

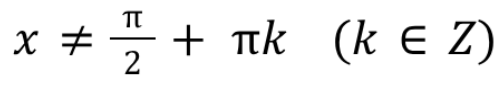
Trig Functions: y=tan(x) range

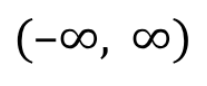
Reciprocal Trig: sine vs cosecant

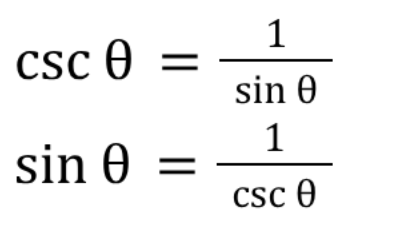
Reciprocal Trig: cosine vs secant

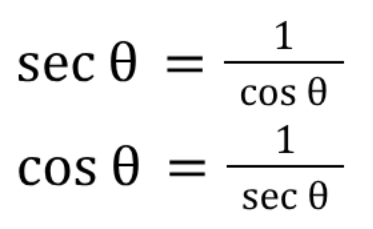
Reciprocal Trig: tangent vs cotangent

Inverse Trig: y=sin^-1(x) domain

[-1, 1]

Inverse Trig: y=sin^-1(x) range

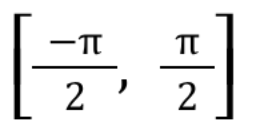
Inverse Trig: y=cos^-1(x) domain

[-1, 1]

Inverse Trig: y=cos^-1(x) range

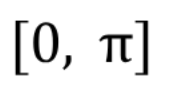
Inverse Trig: y=tan^-1(x) domain

Inverse Trig: y=tan^-1(x) range

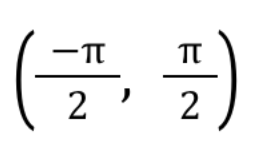
SAS Area Formula

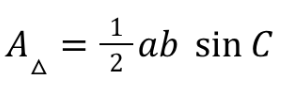
Law of Sines

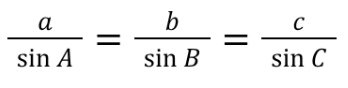
Law of Cosines

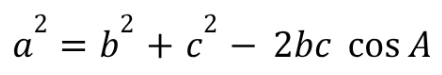
Sinusoidal Functions: equations

• y=A(b(x-c))+D

• y=A(b(x-c))+D

Sinusoidal Functions: A

Amplitude: Vertical distance between midline and max (or min) (Half the difference between the max and min values)

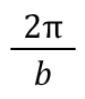
Sinusoidal Functions: b (in relation to pi)

Period: Horizontal distance it takes for the function to repeat

Sinusoidal Functions: c

phase shift: Horizontal distance the graph is moved left or right

Sinusoidal Functions: D

vertical displacement: Vertical Distance graph is moved up or down (midline) (The average of the max and min values)

Pythagorean Identities (3)

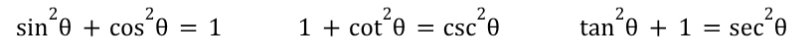
Even / Odd ID: sine

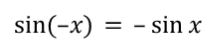
Even / Odd ID: cosine

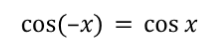
Even / Odd ID: tangent

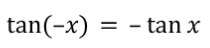
Co-Function ID: sine