A Level Physics - Materials

Hooke's Law

the extension of a spring is directly proportional to the force applied up until the elastic limit

Force constant units

Nm-1

Hooke's Law equation

F = kx

What is k called for springs?

spring constant

Tensile deformation

extension

Compressive deformation

compression

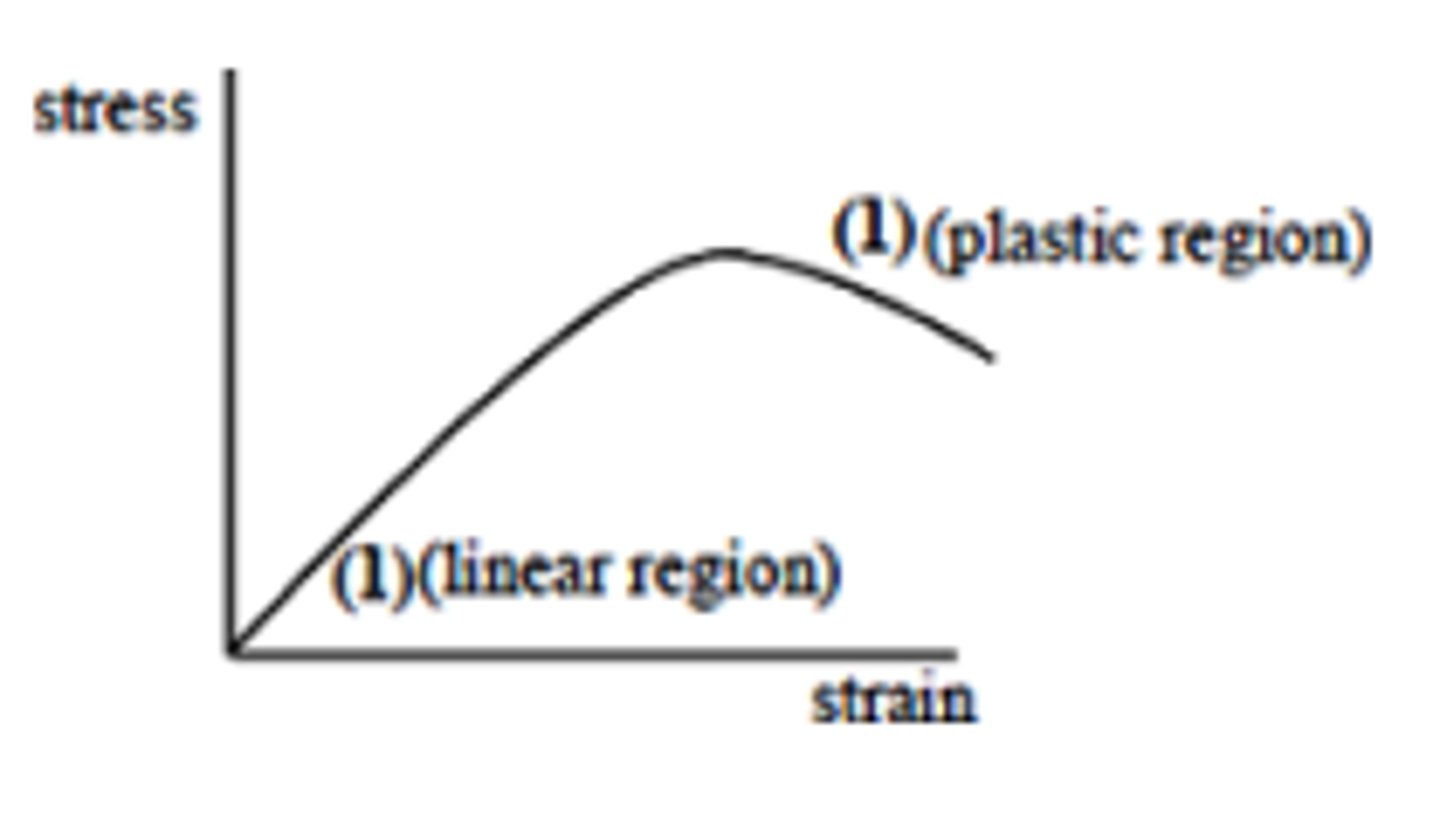
Limit of proportionality

obeys Hooke's law, but undergoes elastic deformation

What happens after the elastic limit is reached?

plastic deformation

Springs in series

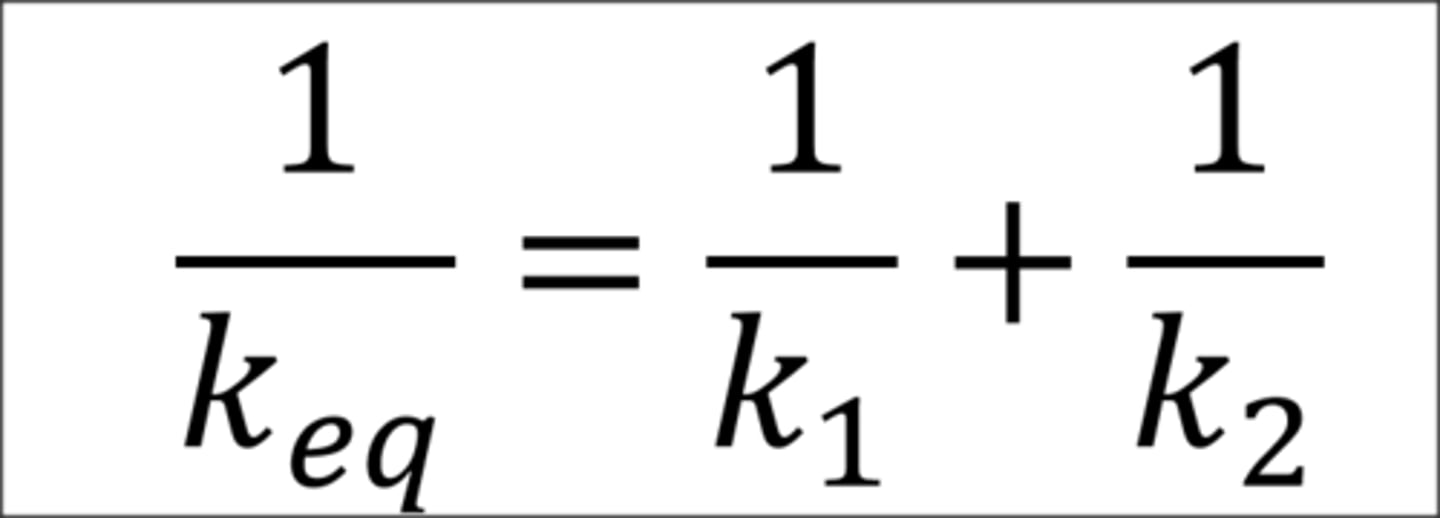
Springs in parallel

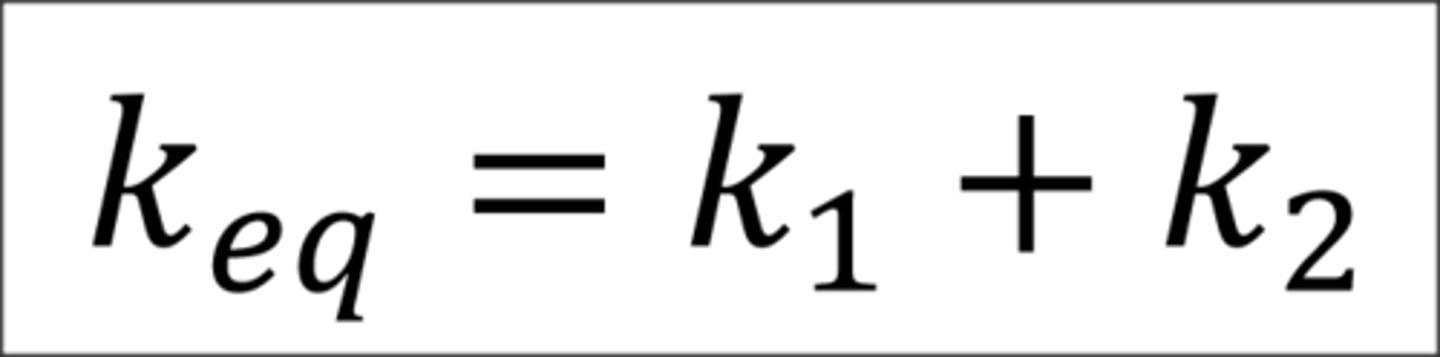
Elastic deformation

material returns to its original shape once the forces are removed

What happens to molecules in elastic deformation?

• atoms are pulled apart when force is applied

• atoms move slightly relative to their equilibrium position

• atoms return to equilibrium position when force is removed

Plastic deformation

permanent deformation

What happens to molecules in plastic deformation?

atoms have been moved permanently

Experiment to investigate extension

• hang spring from a clamp and attach meter ruler to clamp stand

• add weights to the end of the spring

• extension = new length - original length

• plot force-extension graph

• gradient = k

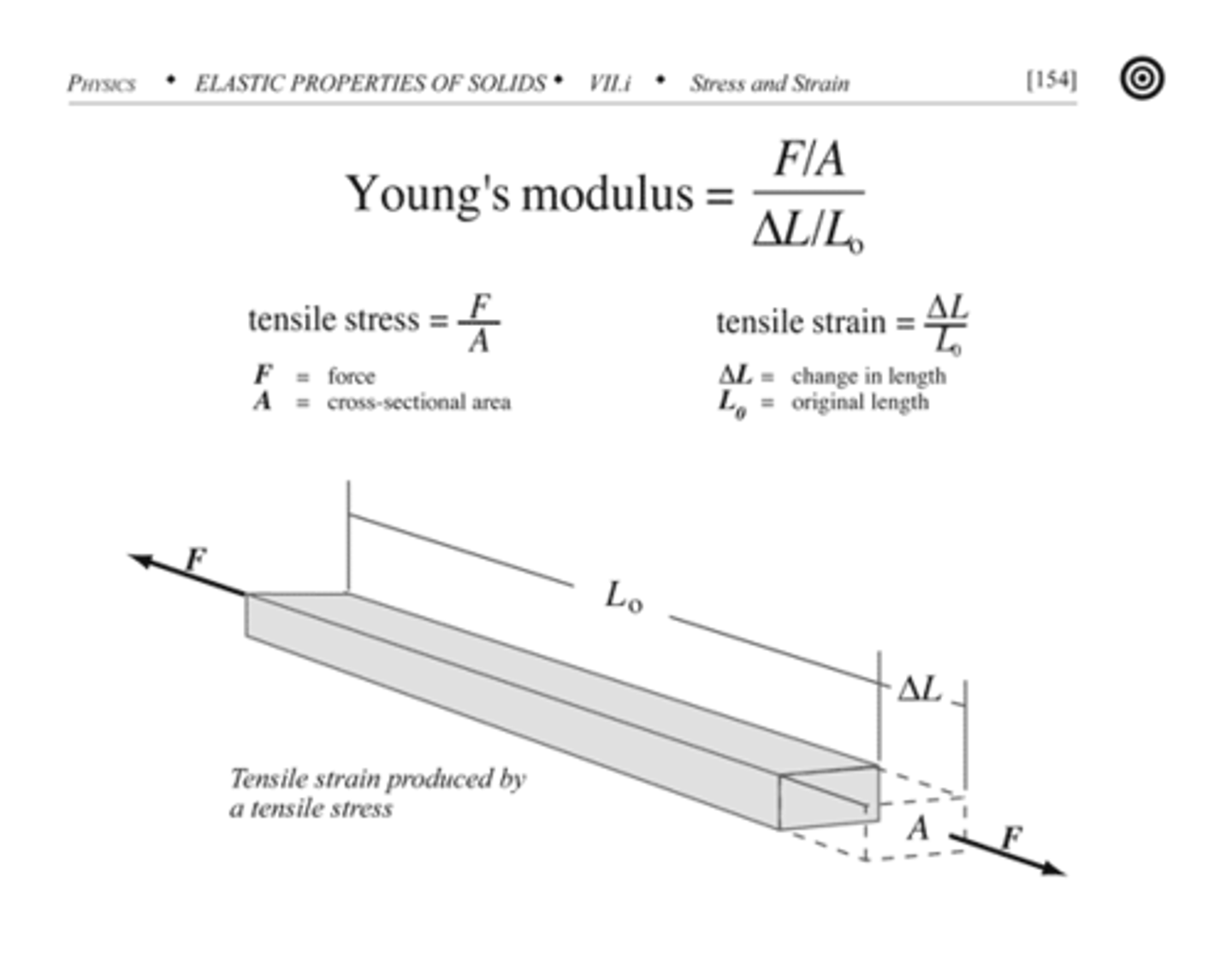
Tensile stress

σ = F/A

Units of stress

Nm-2 or Pa

Tensile strain

strain = extension/original length

ε = x/l

Units of strain

no units

Ultimate tensile strength

the maximum stress the material can withstand before breaking

Area of a force-extension graph

work done (elastic potential)

Derive E = (1/2)kx^2

work done = area of force-extension graph = 0.5Fx = 0.5kx^2

What is work done in stretching or compressing a material stored as?

elastic potential

Young modulus

stress/strain

units of Young modulus

Nm-2 or Pa

Experiment to find Young Modulus

• measure diameter of wire using micrometer to find cross sectional area

• start attach small weight to end to straighten the wire

• measure initial length

• increase weight in steps and record extension (stretched - unstretched)

• calculate stress and strain

• plot stress-strain graph and find gradient

Area under a stress-strain graph

elastic potential energy stored per unit volume

Ductile material

Brittle material

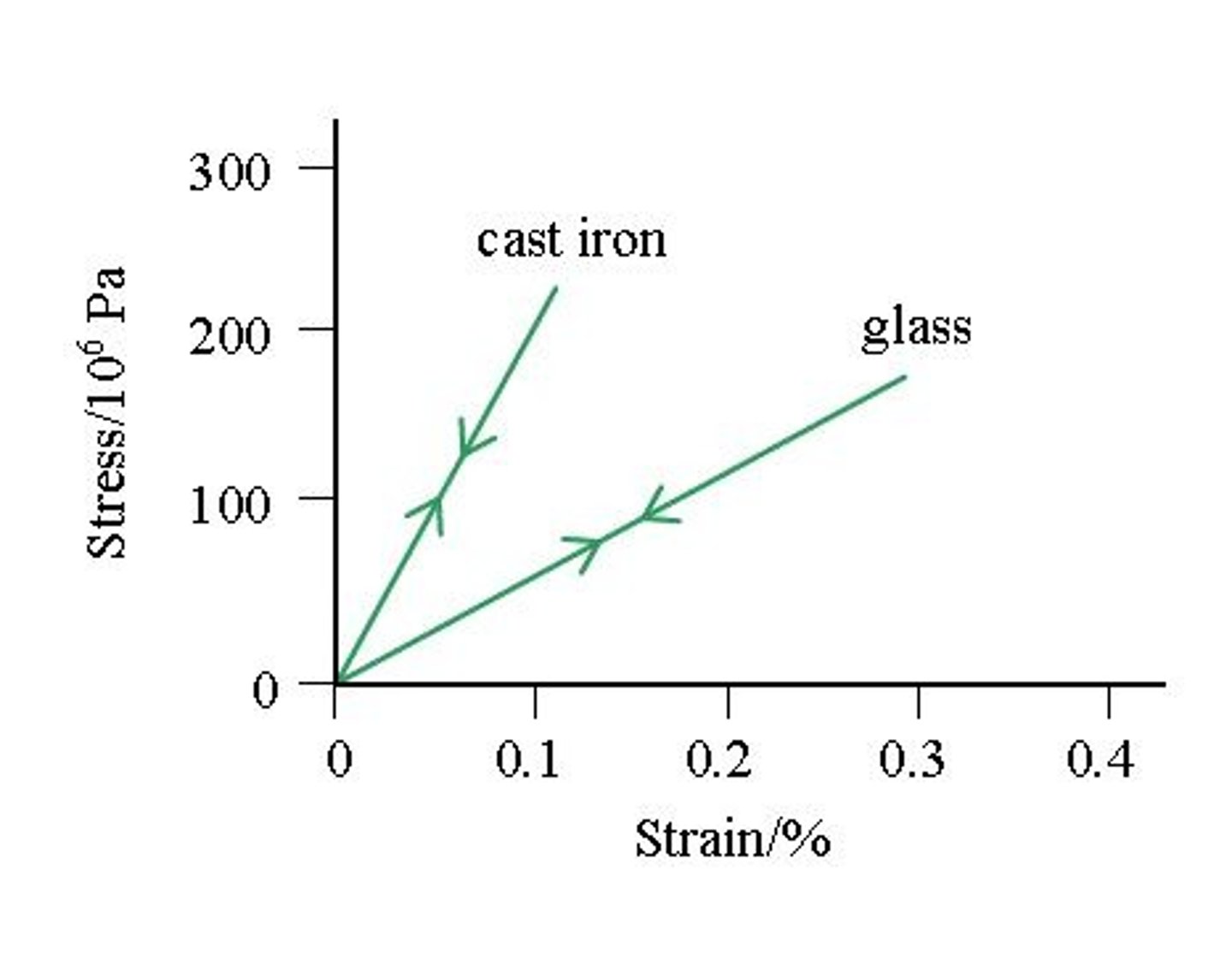
Yield point

stress at which a large amount of plastic deformation takes place with a constant/reduced load

Polymeric materials

molecules are arranged in long chains

Area between loading and unloading curves

amount of energy converted to heat per unit volume

Crack propagation

Existing microscopic cracks in a material, grows because of stress and leads to fracture

Crystalline

Ordered Structure making a crystal lattice, Ductile and tough. E.g metals

Amorphous

Non- ordered structure, rigid structure directional covalent bonds E.G ceramics/glass

Polymeric

Long- chain, Strong and flexible. Cross links can be added to make them stronger.

Foreign atoms

Fills gaps → less movement and more grain boundaries.

Grain boundaries

regions between individual crystals (grains) in a polycrystalline material where the atomic arrangement is irregular or misaligned

Necking

Cross-sectional area of a metal that reduces as it plastically deforms

How does Crack propagation cause brittle fracture?

Small imperfections lead to cracks on the surface of materials. →brittle fracture- hardly extends then breaks

Rubber

Low Young Modulus

Hysteresis

Stress-Strain graph is different for loading and unloading.