Chapter 7: The Central Limit Theorem

Introductory

• Central limit theorem: If the sample size is large enough then we can assume it has an approximately normal distribution.
  • The sample size has to be greater than 30 to assume an approximately normal distribution
• Exponential Distribution: a continuous random variable (RV) that appears when we are interested in the intervals of time between some random events

7.1 The Central Limit Theorem for Sample Means (Averages)

• μX = the mean of X

• σX = the standard deviation of X

• 𝑥¯ ~ N**(𝜇𝑥, 𝜎𝑋 / 𝑛√)** = If you draw random samples of size n, then as n increases, the random variable 𝑥 which consists of sample means, tends to be normally distributed

• sampling distribution of the mean: approaches a normal distribution as n, the sample size, increases.

• The random variable 𝑥¯ has a different z-score associated with it from that of the random variable X. The mean 𝑥¯ is the value of 𝑥¯ in one sample.

  

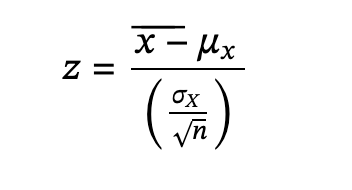
• μX = the average of both X and x¯

• Standard error of the mean: 𝜎𝑥 = 𝜎𝑋 / √𝑛 =standard deviation of x¯

• Probabilities for means on the calculator

  • 2nd DISTR
  • 2:normalcdf
  • normalcdf (lower value of the area, upper value of the area, mean, standard deviation / √sample size)
  • where
  • mean is the mean of the original distribution
  • standard deviation is the standard deviation of the original distribution
  • sample size = n

• Percentiles for means on the calculator

  • 2nd DISTR
  • 3:InvNorm
  • k = invNorm (area to the left of 𝑘, mean, standard deviation / √sample size)
  • Where→
  • k = the kth percentile
  • mean is the mean of the original distribution
  • standard deviation is the standard deviation of the original distribution
  • sample size = n

7.2 The Central Limit Theorem for Sums

• The central limit theorem for sums: As sample sizes increase, the distribution of means more closely follows the normal distribution.

  • ∑X ~ N[(n)(μx),(𝑛√n)(σx)]

• The normal distribution: has a mean equal to the original mean multiplied by the sample size and a standard deviation equal to the original standard deviation multiplied by the square root of the sample size**.**

• The random variable ΣX has the following z-score associated with it:

  • Σx is one sum.
  • 𝑧 = 𝛴𝑥–(𝑛)(𝜇𝑋) / (√𝑛)(𝜎𝑋)
  1. (n)(μX) = the mean of ΣX
  2. (√n)(𝜎X) = standard deviation of ΣX

• Probabilities for sums on the calculator

  • 2nd DISTR
  • 2: normalcdf (lower value of the area, upper value of the area, (n)(mean), (√n)(standard deviation))
  • where:
  • mean is the mean of the original distribution
  • standard deviation is the standard deviation of the original distribution
  • sample size = n

• Percentiles for sums on the calculator

  • 2nd DIStR
  • 3:invNorm
  • k = invNorm (area to the left of k, (n)(mean), (√n)(standard deviation)
  • where:
  • k is the kth percentile
  • mean is the mean of the original distribution
  • standard deviation is the standard deviation of the original distribution
  • sample size = n

7.3 Using the Central Limit Theorem

• Law of large numbers: if you take samples of larger and larger size from any population, then the mean x¯ of the sample tends to get closer and closer to μ.
• Binomial distribution:
  • there are a certain number n of independent trials
  • the outcomes of any trial are success or failure
  • each trial has the same probability of a successful p

Examples

\
\
\