5: magnetic resonance

describe types of atomic/molecular interaction at different areas of EM spectrum

radio = NMR

microwave = EPR

microwave = molecular rotation

IR = molecular vibration

UV/Vis = valence e- excitation

x-rays = core e- excitation

the type of EM radiation is dependent on the size of the energy gap of transition being probed

describe NMR vs EPR

NMR = spectroscopy of nuclear spin states in a magnetic field

EPR = spectroscopy of electron spin states in a magnetic field

describe magnetic vs electric dipoles

electric dipoles = arise from two equal and opposite electric charges separated by a small distance

magnetic dipole = arise from spinning charged particle generating an magnetic field

describe NMR/EPR vs other types of spectroscopy

other = electric dipole moments interacting with electric component of EM radiation

NMR/EPR = magnetic dipole moment (electron/nucleus) interacting with magnetic component of EM radiation

describe classical angular momentum

an object rotating around a point has angular momentum

= vector = magnitude and direction

two types

• spin AM = mass spinning on axis

• orbital AM = mass orbiting a central point

describe the application of the rigid rotor model

to model angular momentum in rotating diatomic molecule

describe the difference in angular momentum between molecules and elementary particles

molecules = acquire rotational angular momentum (by collisions)

elementary particles = intrinsic angular momentum (spin)

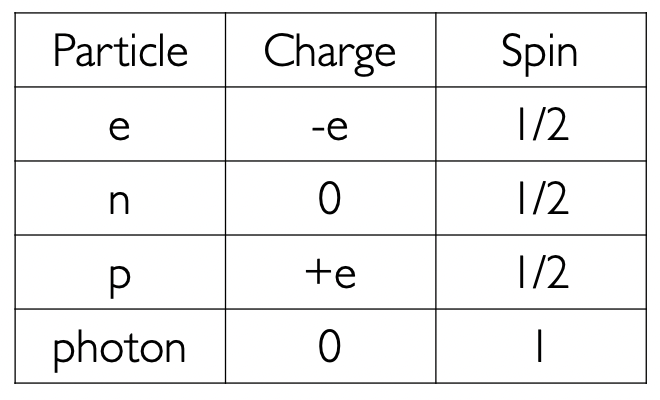
what are charge and spin for the elementary particles

describe how to differentiate vectors and quantum numbers

vectors = bold

quantum numbers = italics

describe nuclear spin

nuclear spin = intrinsic angular momentum = I

since it is angular momentum:

= vector = magnitude and direction

what equation defines the magnitude of I? (given)

I = spin quantum number

hence, the magnitude of spin is constant for a given nuclei

only direction can be changed

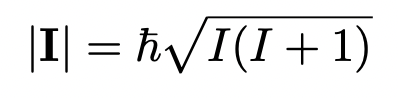
describe spin quantum number

unique to a given nuclei

= determined primarily by number of protons/neutrons

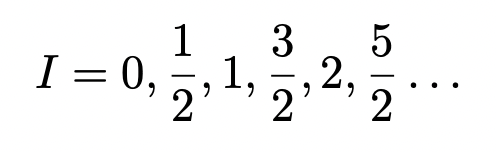
what nuclei are NMR active?

I > 0

= odd mass number

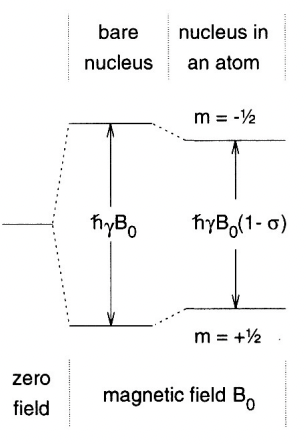
describe Zeeman splitting

• a nuclei with spin I is (2I + 1) degenerate due to m(I)

• application of magnetic field breaks the degeneracy

• gives rise to ‘Zeeman eigenstates’

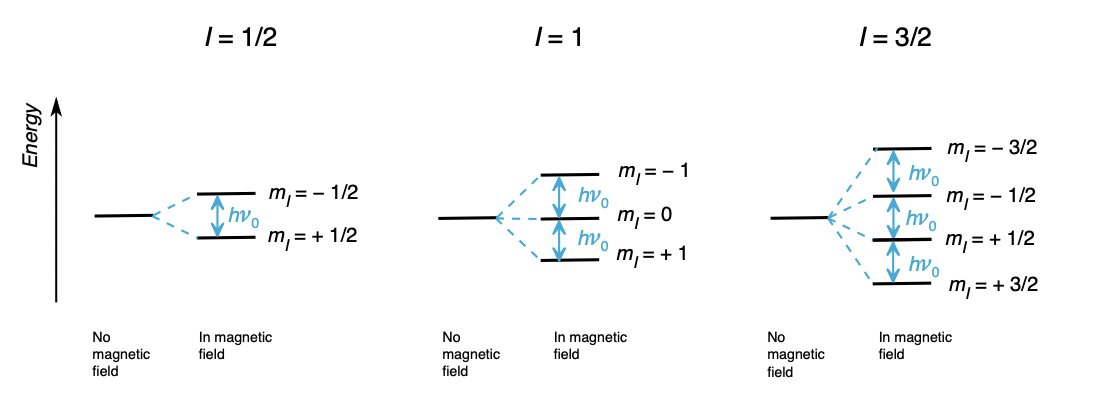
describe m(I)

m(I) = nuclear azimuthal/magnetic quantum number = describes orientation of nuclear spin (vector) in a magnetic field

= -I, -I+1, …, +I

what equation defines the energy of the Zeeman eigenstates?

m(I) = controls number of Zeeman eigenstates
γ = gyromagnetic ratio = unique for a nucleus = controls extent of Zeeman splitting (size of E gap between eigenstates)

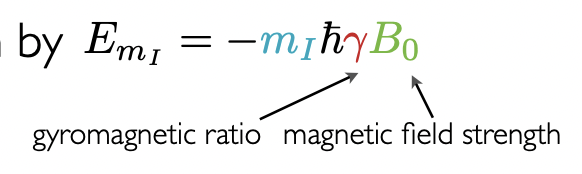
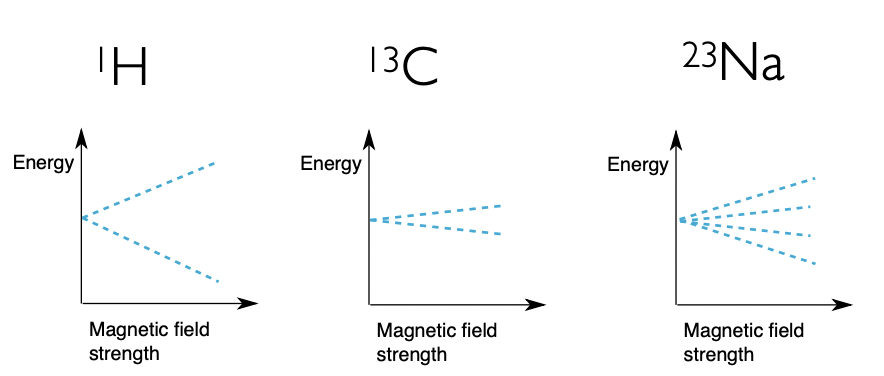
describe what varies the Zeeman eigenstates here

(1)H and (13)C:

= same I = same m(I) = both split to 2 sublevels

= different γ = different energy gaps

(13)C and (23)Na:

= similar γ = similar energy gaps

= different I = different m(I) = split into different no. of sublevels

what are the selection rules for a nuclei’s NMR activity?

• I > 0 (odd mass number)

• Δm(I) = ± 1

describe the energy difference between allowed Zeeman eigenstates

(using m(I) = ½ as basis)

describe the Larmor frequency (conversion to v not given!!)

the frequency of the allowed transition between Zeeman eigenstates for a given nuclei

= frequency of transition between different orientations of nuclear spin (vector) in a magnetic field

(= frequency at which nuclear spins precess in a magnetic field)

= constant for a given nucleus

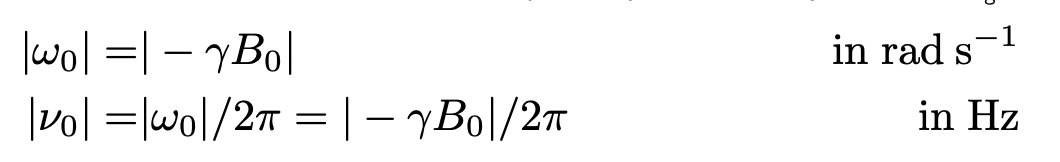
what units are B(0) in?

tesla (T)

what does the value of the Larmor frequency of many common nuclei tell us?

= fall in radio part of EM spectrum

= radio used in NMR/EPR

what is unit M (mega)?

10^6

describe the relationship between spin and magnetism

= spinning charge (internal angular momentum), I, gives magnetic moment

= magnetic moment, μ, of a nucleus is proportional to spin angular momentum, I

gyromagnetic ratio = constant of proportionality

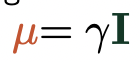
describe the possible values of gyromagnetic ratio

μ points in same direction as I = +ve γ

μ points in opposite direction of I = -ve γ

describe a and B Zeeman eigenstates

alpha (a) = ‘up’ = +ve m(I)

beta (B) = ‘down’ = -ve m(I)

describe the configuration of Zeeman eigenstate depending on values of gyromagnetic ratio

+ve γ = μ points in same direction as I

-ve m(I) (B) higher in energy (harder to flip)

-ve γ = μ points in opposite direction of I

+ve m(I) (a) higher in energy (harder to flip)

describe the problem with the energy level approach

nuclei do not have to be in just one of these two states (up or down)

= mixture of wavefunctions associated with each energy level

i.e. coherent superposition/mixed state

what is spin polarisation

alignment of nuclear spins in response to application of a magnetic field

describe the direction of spin angular momentum vector, I, with magnetic moment vector, μ

+ve γ = μ parallel to I

-ve γ = μ anti-parallel to I

describe nuclei spins in absence of magnetic field

spin polarisation axes (spins, I) pointing in all possible direction

= no net magnetisation

what happens when a magnetic field is appled?

the spin polarisation axes (spins, I) precess around the axis of magnetic field B(0)

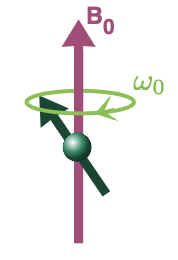
describe the frequency and angle of precession

frequency of precession = Larmor frequency

angle of precession = dependent on initial spin direction

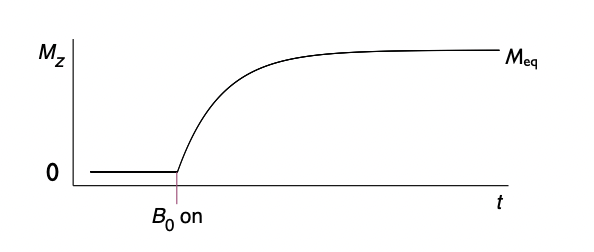
describe longitudinal relaxation

precession around axis of magnetic field = minimises energy of interaction between the spin magnetic moment and magnetic field = lower energy orientation

net magnetisation grows along z axis as spins come to equilibrium with magnetic field B(0)

= contributes to bulk magnetisation vector, M, which precesses around axis of magnetic field

draw a graph representing longitudinal relaxation

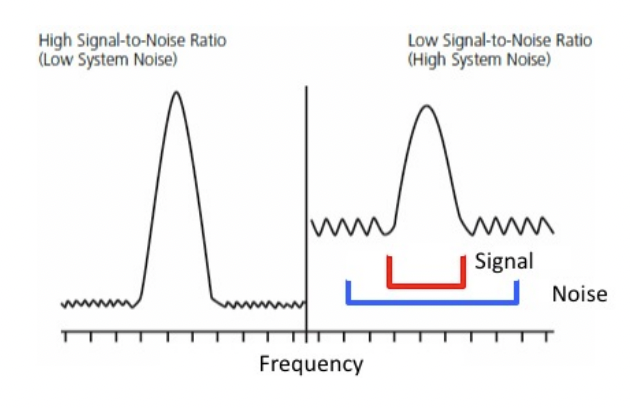
describe signal:noise ratio

high signal:noise ratio desired

describe population distributions between Zeeman eigenstates

remember ΔE = h|v(0)|

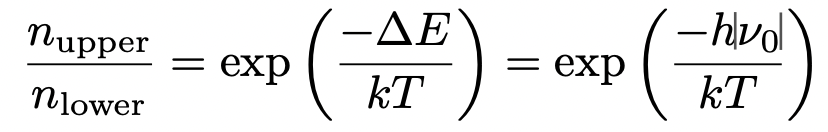
describe how population differences lead to bulk magnetisation vector

population differences between different Zeeman eigenstates = different m(I) values = different alignment to external magnetic field

n(upper) = excited state = anti aligned with B(0)

n(lower) = ground state = aligned with B(0)

the population difference is the difference in alignment to external magnetic field = bulk magnetisation vector, M

always more aligned (n(lower)) since lower energy configuration

describe the size of population differences in NMR

very small = inherently insensitive

= small bulk magnetisation vector

what increasing the sensitivity of NMR for certain nuclei?

 higher gyromagnetic ratios, γ

describe detection in NMR

1. external magnetic field (B(0)) is applied

= creates bulk magnetisation vector = precess at Larmor frequency due to small population difference

= aligns nuclear spins at equilibrium

2. RF (radiofrequency) pulse at Larmor frequency tips magnetisation away from B(0) axis, causing bulk magnetisation vector M to precess in the transverse plane (xy) at Larmor frequency

3. precessing magnetisation creates an oscillating magnetic field that induces current in receiver coil = free induction signal (FID)

what expression describes the lifetime of the transverse component of bulk magnetisation (NOT GIVEN)

M(t) = bulk magnetisation at time t

M(0) = bulk magnetisation at time 0 (after RF pulse)

w = Larmor frequency

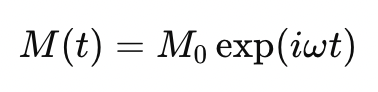
how can exp(iwt) be expressed alternatively?

using Euler’s formula

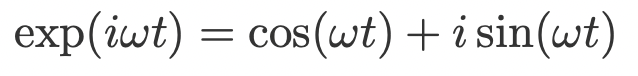
describe free induction decay (FID)

= complex and time-dependent (since transverse component of bulk magnetisation decays over time)

M(y) = real component

M(x) = imaginary component

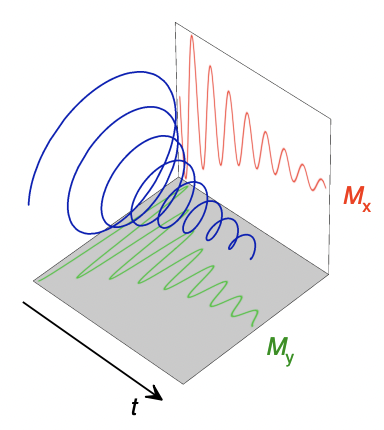
explain the application of the Fourier transform on free induction decay

to convert free induction decay (FID):

time domain signal → frequency domain spectrum

describe pulse acquisition diagrams

visualise sequence of events during NMR experiment

what process can improve SNR (signal:noise ratio)

signal averaging

describe signal averaging

• experiment repeated multiple times = scans/transients

• transients added up

SNR ∝ √number of transients

what is required of a magnetic to be a magnetic field in an NMR experiment?

• strength

• homogeneity

• stability

what types of magnets can be used in NMR?

• permanent (<1.5 T)

• electromagnetic (<2.5 T)

• superconducting (<23.5T) best on all criteria

describe NMR probes

• contain rf coils (applied rf pulse AND receives signal)

• houses the sample

• can spin and vary temp

describe continuous wave (CW) and Fourier transform (FT) NMR

CW NMR: either

• keep B(0) constant and vary frequency of rf pulse

• keep frequency of rf pulse constant and vary B(0)

FT NMR:

• range of rf pulse frequencies applied at once

what are the components of the electric/magnetic field experienced by a nuclear spin?

• external field

• the sample itself (internal)

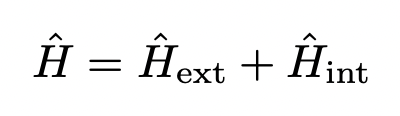
compare solution state vs solid state NMR

solution state = anisotropies are averaged

solid state = anisotropies are NOT averaged = more complex

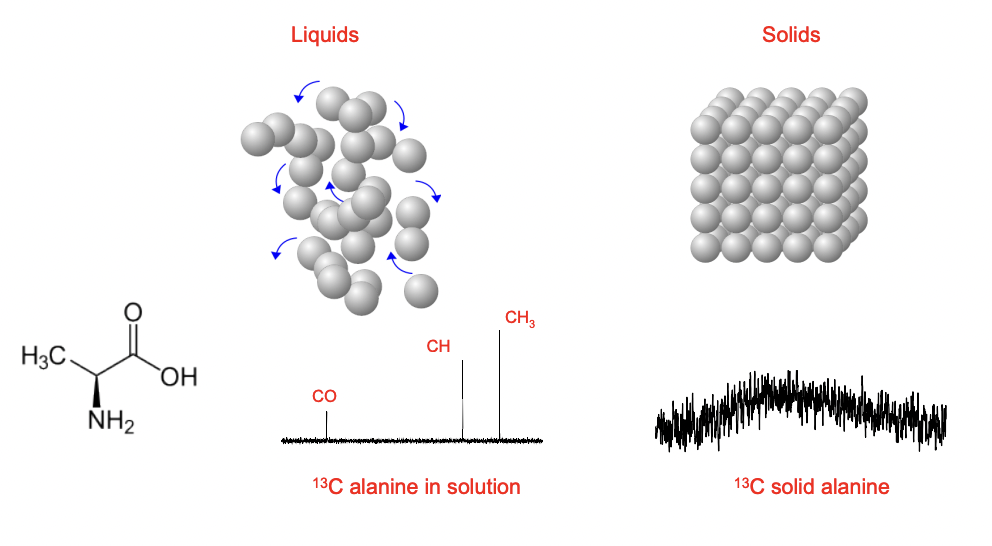
describe the effect of a nuclei’s local distribution

the local electron distribution around a nucleus effects the resonance frequency at which it processes around the external field

theory = 1H at B(0) = 9.4T should resonate at 400MHz

B(in) = induced magnetic field from external magnetic field caused by circulation of electrons in their AO/MOs

B(in) either opposes (shields = lowers B) or augments (deshields = increases B) the external field

B = effective field

define effective field at nucleus

B = effective field

B(0) = external magnetic field

B(in) = induced magnetic field

σ = shielding

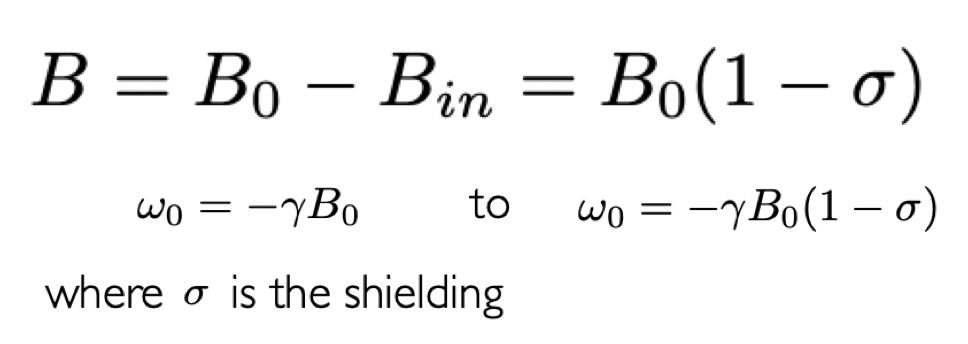
describe the effect of shielding

shielding reduces the Larmor frequency of a nucleus

= reduces the energy gap between Zeeman eigenstates

define chemical shift (given)

( / v(spectrometer) ) removes the dependence on the external field

defines the difference in Larmor frequency of a nucleus w.r.t. a reference

= define the extent of shielding

describe shielding in atoms vs molecules

atoms = simple = only diamagnetic shielding

molecules = complex (motion of electrons more complex) = diamagnetic and paramagnetic de/shielding

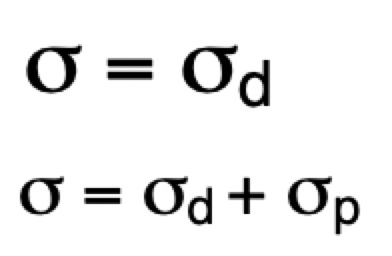
describe diamagnetic and paramagnetic de/shielding

diamagnetic shielding = reduces the strength of the magnetic field = induced magnetic field opposing B(0)

= circulates with atomic and molecular orbitals

paramagnetic deshielding = increases the strength of magnetic field = induced magnetic field in the same direction as B(0)

= circulates between occupied ground state MO and unoccupied excited state MO

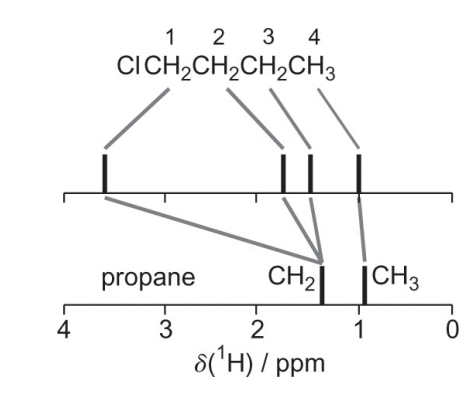
describe the chemical shifts here

diamagnetic shielding effect

aliphatic = circulating electron create B(in) = decrease B(0) = small ppm

Cl = EWG = reduces the shielding/B(in) = larger B(0) w.r.t aliphatic = large ppm

what are different “anomalies” of chemical shift?

• ring current

• H bonding

• paramagnetic compounds

• anisotropy

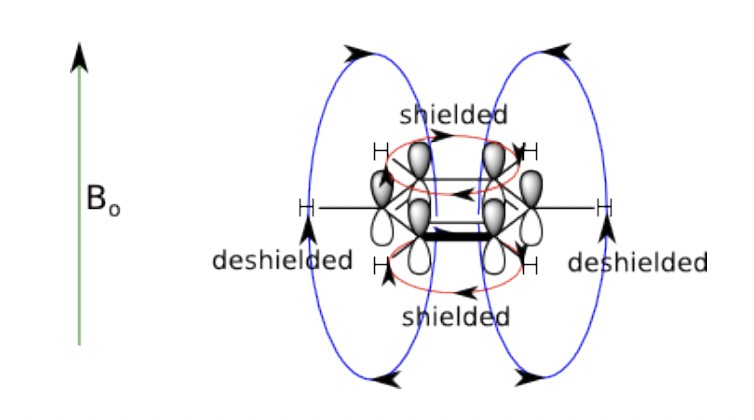
describe ring current

= aromatics

= ∏ electron clouds generate large electronic currents opposing/aligning with external field

downfield = larger chemical shift = larger B(0) than expected = smaller B(in) = ring currents align with and augment B(0)

= shielding effect directly above and below the ring

= deshielding effect in the external plane of the ring

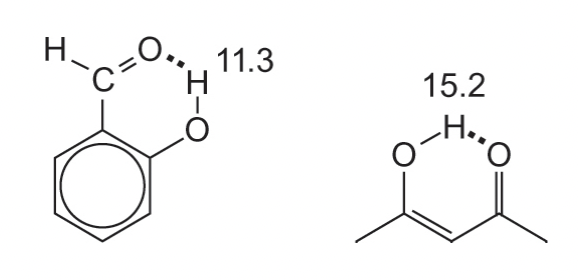
describe hydrogen bonding

= largest (1)H chemical shifts

intramolecular » intermolecular

H bond acceptor draws H away from the heteroatom it is bonded too, reducing the electron density around the H nuclei

= deshielded = smaller B(in) = larger B(0) = larger v(signal) = larger ppm

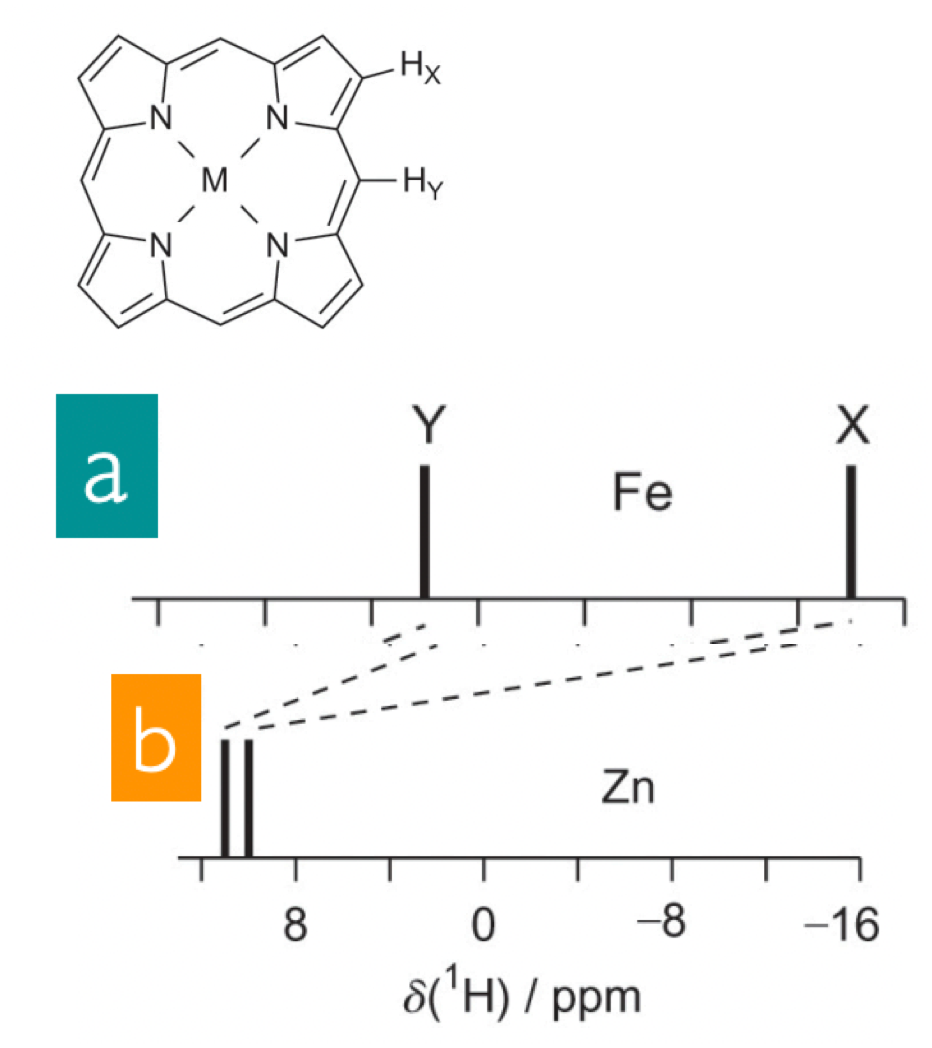
describe paramagnetic compounds

compounds with unpaired electrons generate magnetic field in the presence of external magnetic field

= increase B(in)

= smaller B(0)

= lower ppm = upfield shift

describe anisotropy (CSA = chemical shift anisotropy)

electron density is anisotropic = shielding is anisotropic = orientation dependent

liquids = rapid tumbling = anisotropic averaging

solids = different orientation of molecule = different amount of shielding

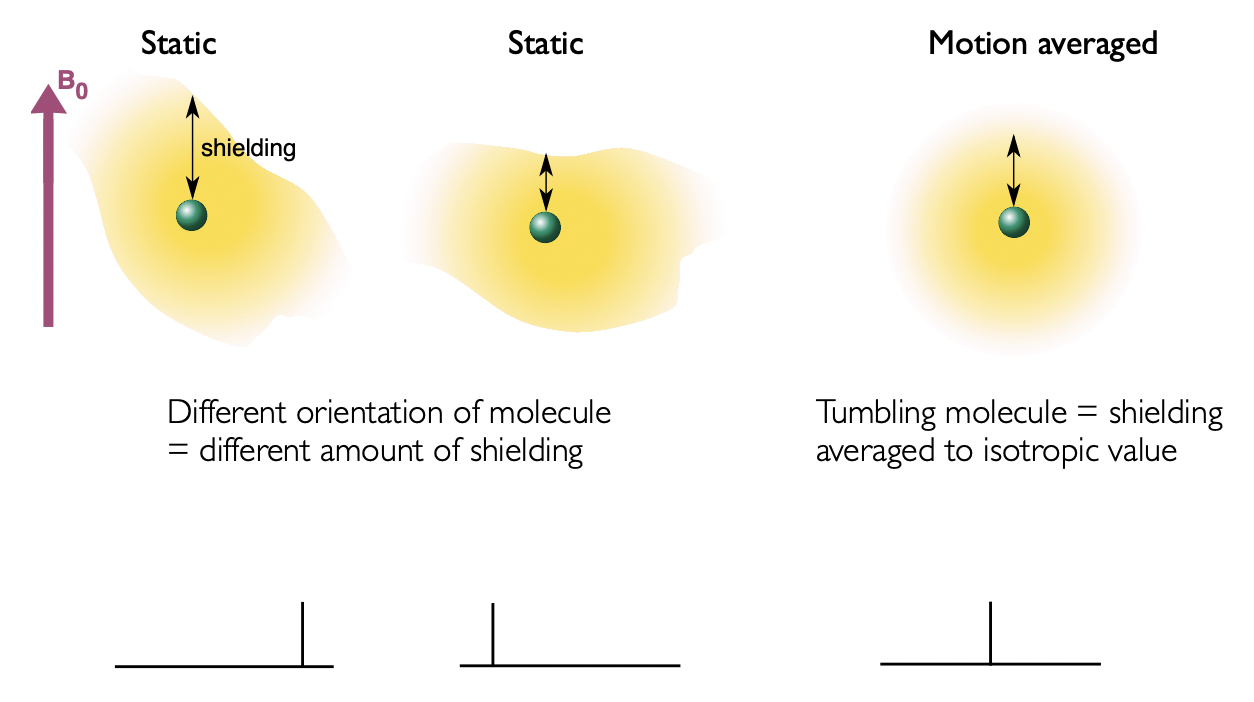
describe CSA in single crystals

single crystals:

= all molecule have the same orientation w.r.t. applied field = equivalent anisotropy = single shift

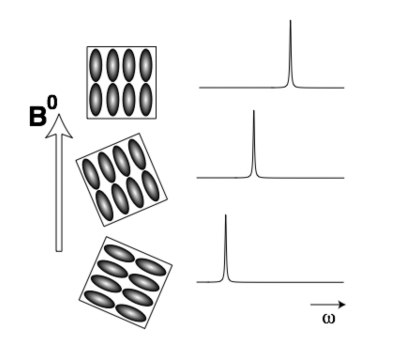
describe CSA in powders

powder:

= millions of randomly orientated single crystals w.r.t. applied field = different shifts

static powder = broad peak

isotropic (all directions) rotation = CSA averages out = single isotropic chemical shift = sharp peak

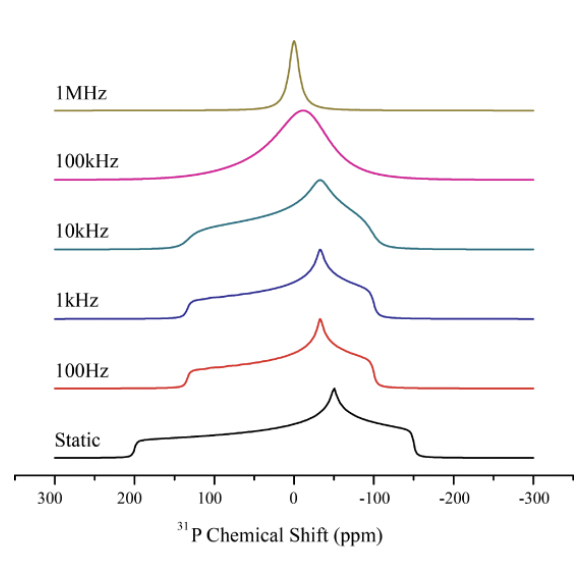
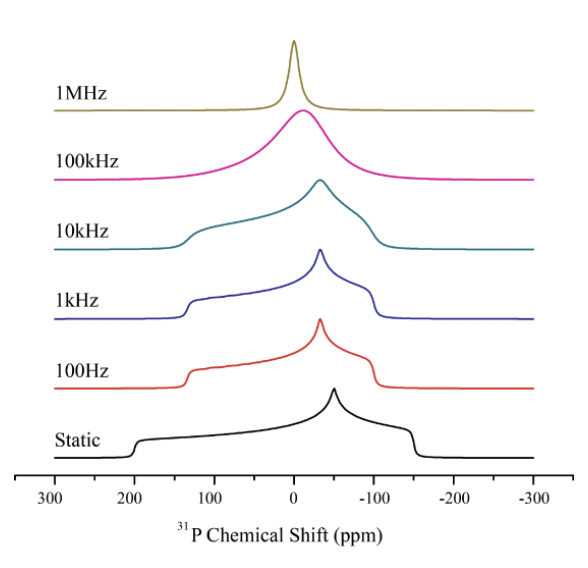
how can the CSA be described here?

Δ = 200ppm ?

δ(iso) = 0 = isotropic chemical shift

η = asymmetry of the chemical shift tensor (the variation from δ(iso)) = 0.5

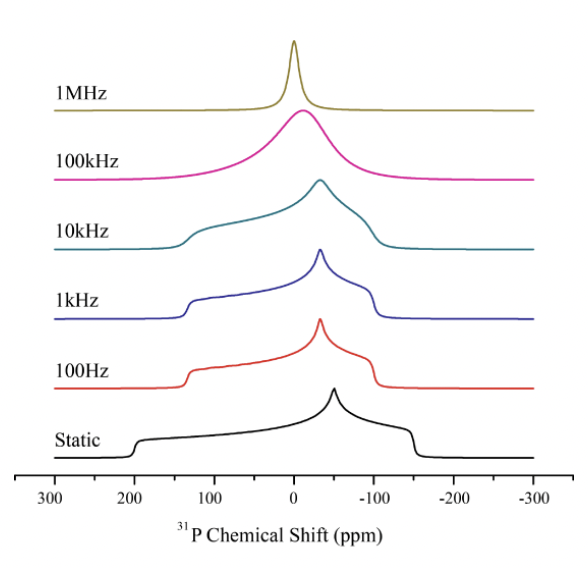
describe dipolar interactions

= through space coupling

= magnetic moment (from spin) created when nuclei/unpaired electrons are placed in magnetic field can interact

= interaction of magnetic moments leads to splitting as there are multiple different arrangement of moments with different energies

i.e. parallel = lower E; anti-parallel = higher E

dipolar interaction ∝ gyromagnetic ratio (∝ magnetic moment)

dipolar interaction ∝ 1/r (distance between nuclei)

dipolar interaction related to θ (angle between nuclei)

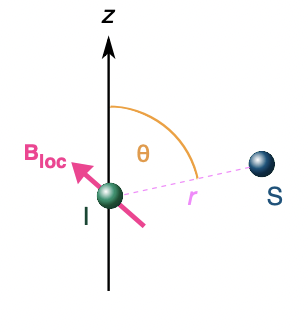
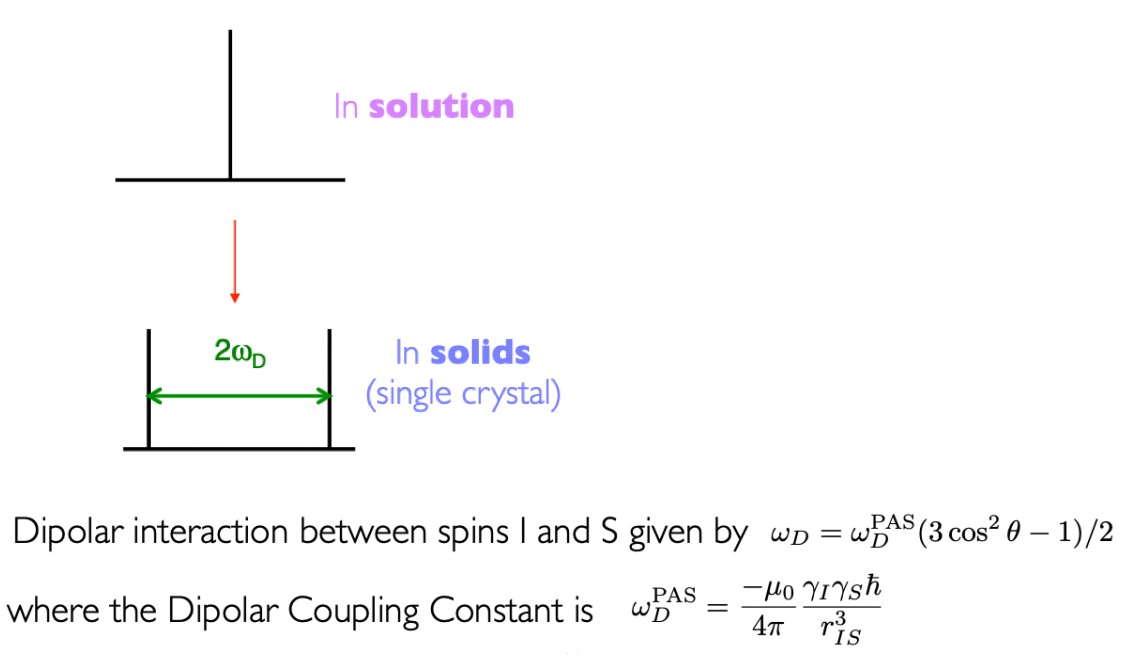
describe dipolar interactions in solution vs solids

solutions = orientations of magnetic dipoles averaged = no interaction

solids = orientations of magnetic dipoles constant = interaction

split by the dipolar coupling constant

describe Pake Doublet

result of dipolar interaction in solid powder samples

powder sample = average of all possible magnetic moment orientations is observed (since magnetic moment/spin is nuclear property not structural)

= varying angles of θ = Pake doublet peak follows cosθ

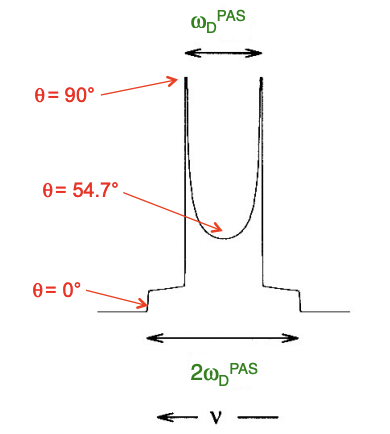
compare powder chemical shift anisotropy vs dipolar interaction anisotropy

CSA: static = broad peak

isotropic rotation = sharp single peak

dipolar interaction anisotropy: static = average = Pake doublet

describe J-coupling

= through bonds

= coupling of pairs of nuclear spins indirectly through electrons in bonding orbitals

= isotropic since through bonds

= independent of B(0) since I does not depend on B(0)

= very weak w.r.t. v(signal) ~10Hz

what is the condition for weakly vs strongly coupled nuclei

weakly: difference in Larmor frequencies greatly exceeds their mutual coupling

strongly: difference in Larmor frequencies similar to their mutual coupling

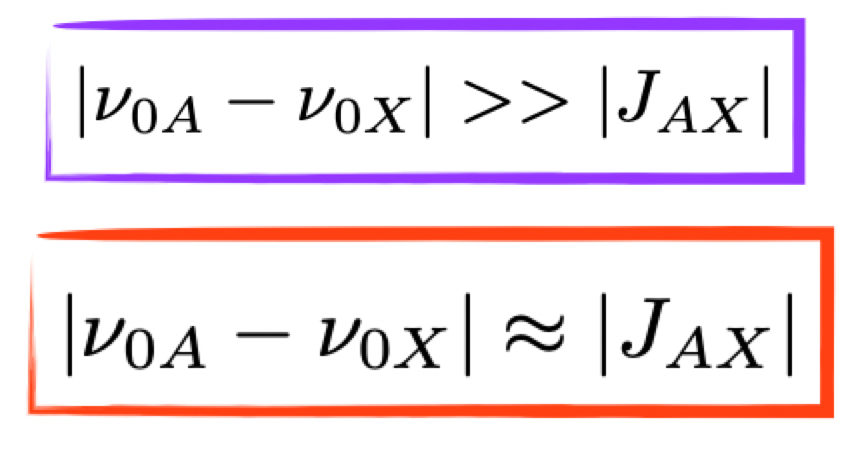
what are the options for coupling of a pair of spin = ½ nuclei?

A = weakly coupled = 2 doublets

B = strongly coupled = intermediate = ‘second-order’ appearance = roof effect

C = magnetically equivalent = 1 singlet

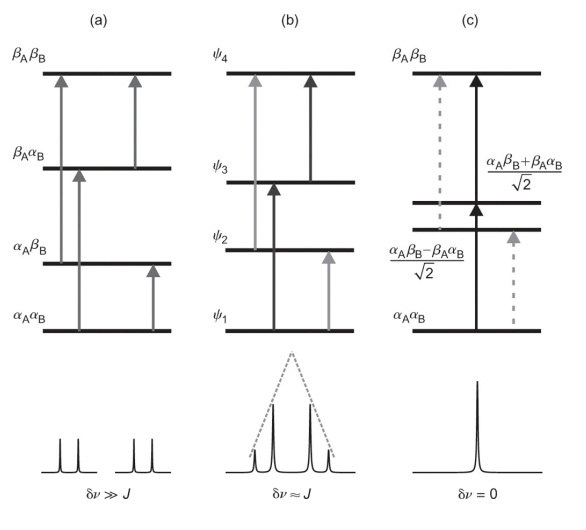
explain multiplet patterns in spin I = 1/2

the number of possible arrangement of spins depends on: I = spin

2I + 1, where I = spin

• 1 nuclei: (I=1/2)

2(1/2) + 1 = 2

2 coupled spins can either be parallel or anti-parallel. this gives rise to a doublet peak.

• 2 x 1 inequivalent nuclei: (I=1/2)

2(1/2) + 1 = 2

2(1/2) + 1 = 2

doublet of doublets

• 2 x equivalent nuclei: (I=1/2)

total I = 1: 2(1) + 1 = 3

triplet

coupling to 1: 2(1/2) + 1 = 2 doublet

coupled to 1: 2(1/2) + 1 = 2 doublet

~doublet of doublets with coinciding central line = triplet

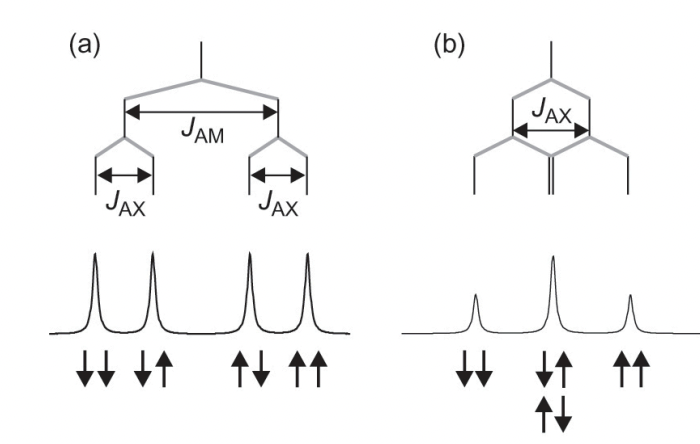
explain multiplet patterns in quadrupolar nuclei (I > 1/2)

= typically obscured by quadrupolar interaction

pattern should follow 2nI + 1

n = number of equivalent spin I nuclei 2

process:

• find multiplicity by 2nI+1

• find pattern to 1 by 2I+1

• repeat for each equivalent nuclei

describe the two types of equivalence

chemical = same electronic environment

magnetic = same interaction with applied magnetic field

describe what happens when B(0) is very weak

Larmor frequency small = chemical shift is small = chance of strong ‘second-order’ appearance increases

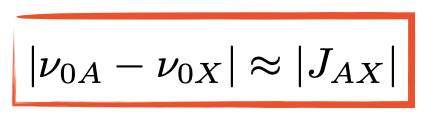
describe features of the roof effect

• intensities of doublet distorted

• doublets no longer centres on chemical shift

describe quadrupolar interaction

quadrupolar nuclei (I>1/2) have non-spherical distribution of charge → electrical quadrupole (eQ) moment

quadrupolar nuclei have:

• magnetic moment (related to spin)

• eQ moment (related to charge distribution)

quadrupolar interaction = eQ moment couples to electric field gradient (EFG) created by electron density surrounding nucleus

= very large up to 50MHz

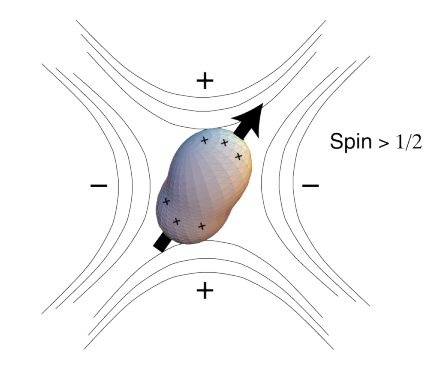
describe quadrupolar interaction in liquids vs solids

quadrupolar interaction is anisotropic with respect to B(0) because the EFG is dependent on the direction of B(0)

liquids = rapid molecular motion = averaged = no interacton

solids = broad lines

describe C(Q) and how it is approximated

C(Q) = quadrupolar coupling constant = describes extent of quadrupolar coupling

C(Q) ∝ size of EFG ∝ 1/symmetry of electron density distribution

EFG can be estimated by the symmetry of the molecule

higher symmetry = smaller EFG = lower C(Q)

lower symmetry = larger EFG = higher C(Q)

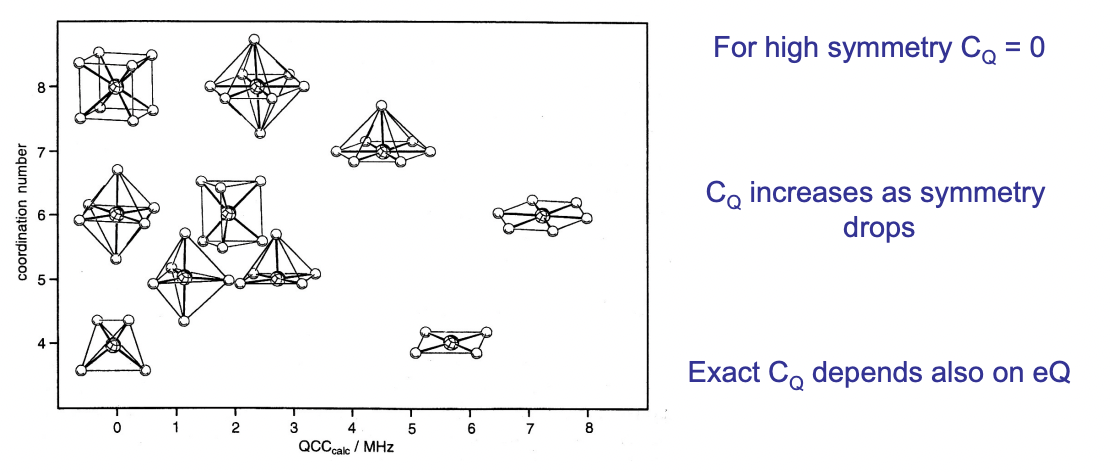
describe the appearance of a peak with quadrupolar interaction

doublet

solids = sharp peaks

liquids = averaged = Pake doublet = defined by cosθ

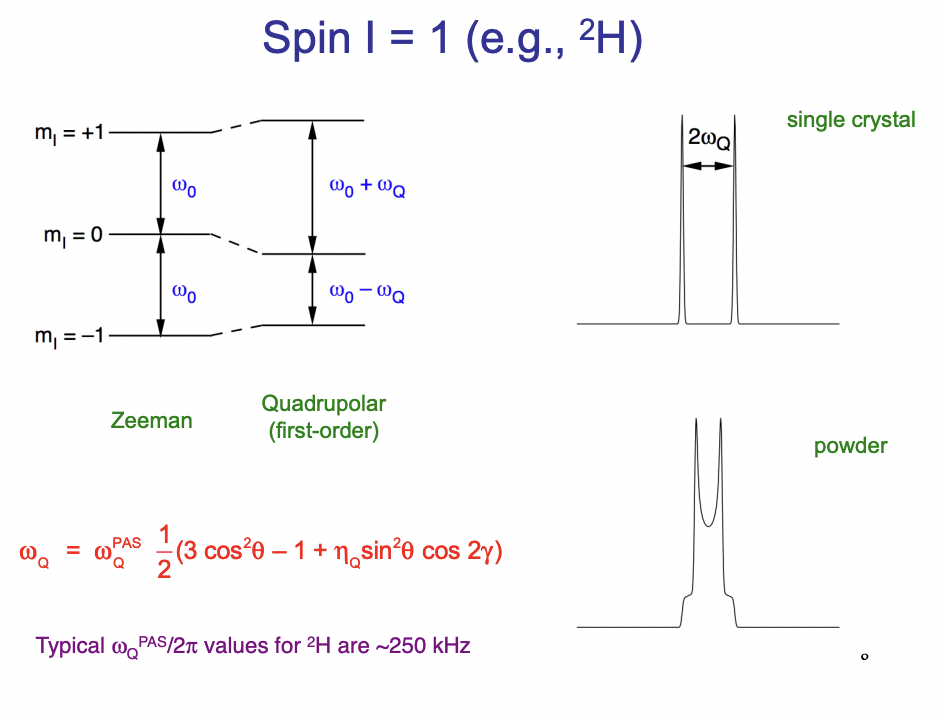
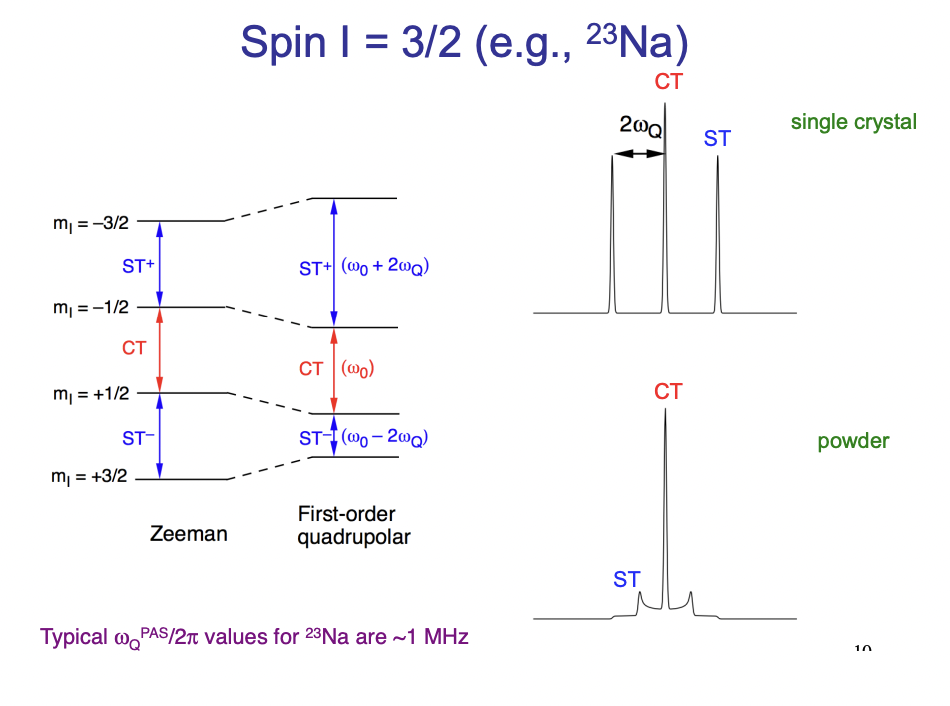
define CT and ST

CT = central transition = between 2 magnetic quantum states (+ve → -ve)

ST = satellite transition = between adjacent m(I) states (+ve → +ve etc.) = more sensitive to quadrupolar coupling

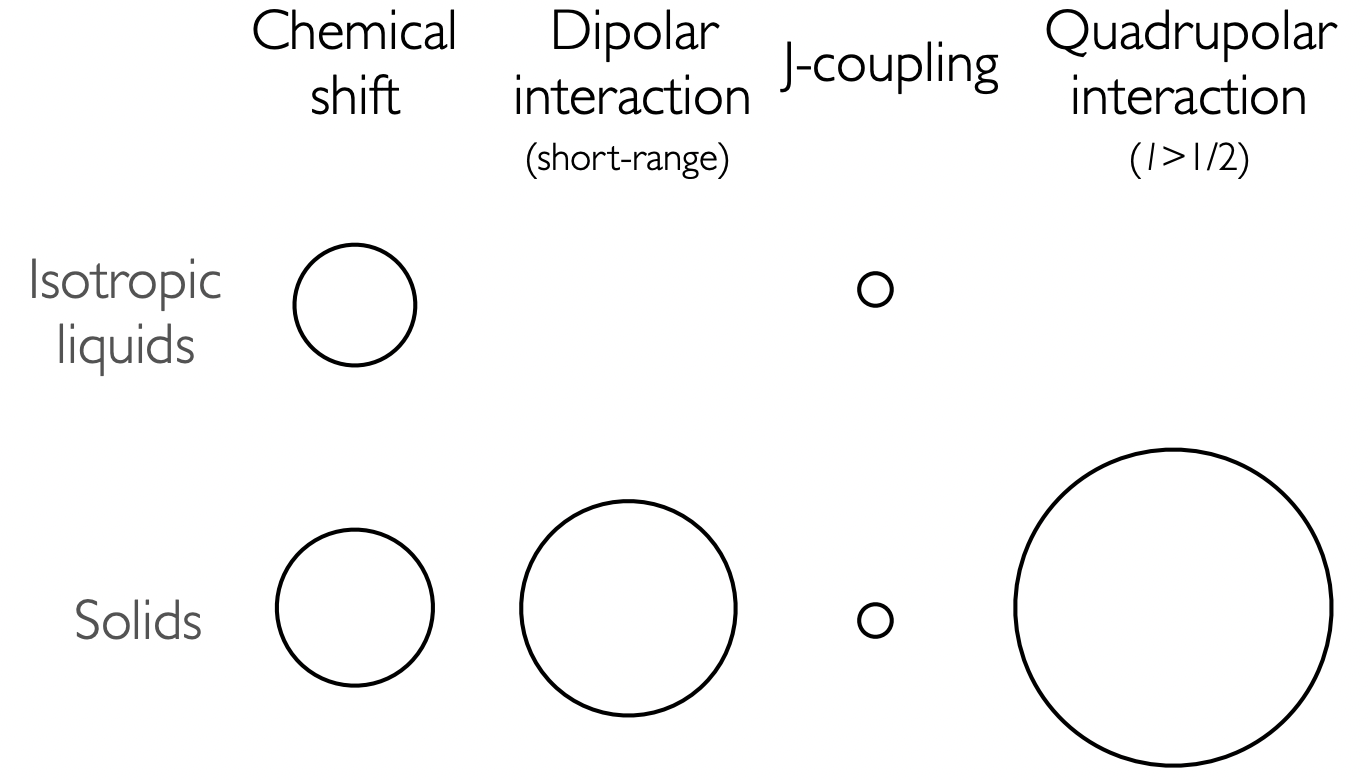
describe the relative magnitude of internal interaction in

• isotropic liquids

• solids

describe relaxation

• spins are aligned to magnetic field B(0) along z-axis = precessing at Larmor frequency = z-magnetisation

• RF pulse is applied along xy plane = x-y magnetisation

• spins relax to ground state = z-magnetisation (NO xy magnetisation)

relaxation is caused by local fields which are different for each spin

what is the conditions for local field inducing relaxation

MUST be at/around the Larmor frequency

describe the two types of relaxation

• spin-lattice (T1)

• spin-spin (T2)

describe spin-lattice relaxation/longitudinal relaxation

z-component of magnetisation coming to equilibrium

local fields cause spin to rotate either:

• TOWARDS z-axis = energy release to surroundings

• AWAY from z-axis = energy investment from surroundings

equal = zero z-magnetisation

lattice is more happy to take up energy than give out energy because it is at thermal/Boltzmann equilibrium = non-zero z-magnetisation (tending towards z-axis)

M(eq) = lattice frequency

describe T1

larger T1 = longer time to reach equilibrium = slower relaxation

smaller T1 = shorter time to reach equilibrium = fast relaxation

what makes spin-lattice relaxation fast?

• fast energy transfer between local fields and lattice (and vice versa)

• B(loc) at the Larmor frequency from CSA/

what are origins of local fields?

anything that causes fluctuations to local magnetic field (stronger) increases relaxation = more chance of approaching Larmor frequecy

• dipolar interaction = magnetic field effected to approach the Larmor frequency

∝ γ(1)γ(2) = extent of interaction

∝ 1/r³

• chemical shift anisotropy (CSA) =

anisotropic nuclei experience slightly different B(0) = B(loc) approaches Larmor frequency

• quadrupolar interaction

very fast relaxation is C(Q)/quadrupolar interaction is large

• paramagnetic species

unpaired electrons produce large magnetic moments which can affect B(loc)

describe spin-spin relaxation/transverse relaxation

decay of xy component of magnetisation to equilibrium value of 0

spins interact with each and cause different local fields in xy plane = precess at slightly different Larmor frequencies = net xy magnetisation decreases over time

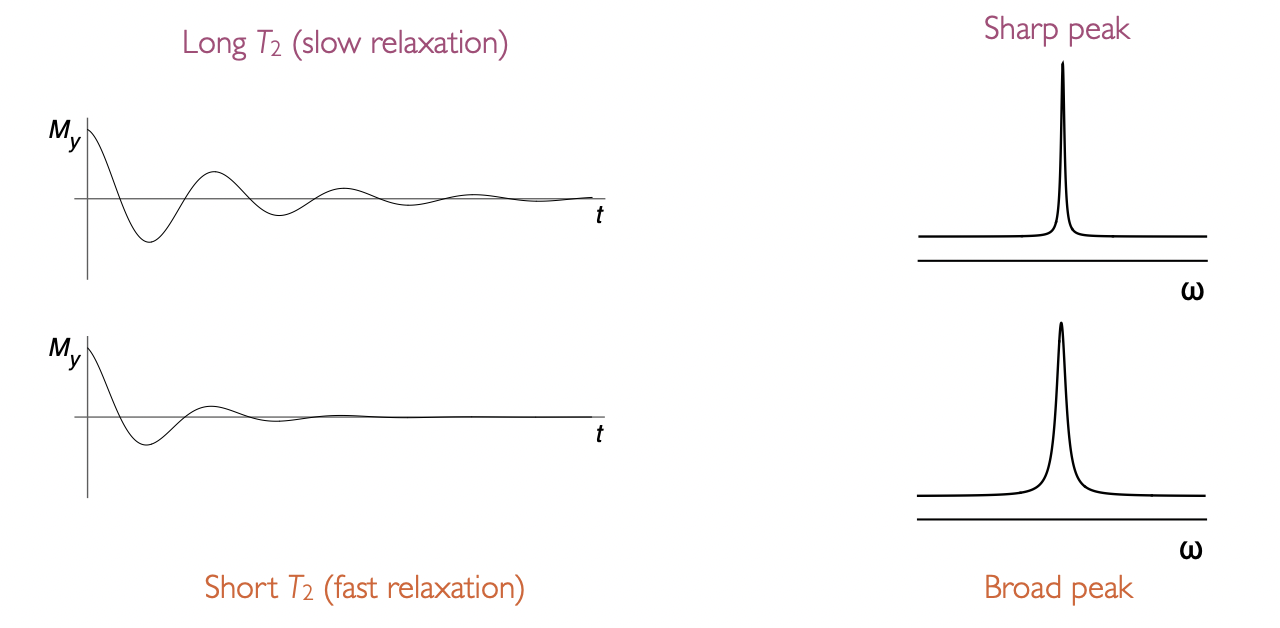
describe T2

larger T2 = longer time to reach equilibrium = slower relaxation

smaller T2 = shorter time to reach equilibrium = fast relaxation

describe the appearance of peak with T2

gives linewidth

long T2 = slow relaxation = sharp peak

short T2 = fast relaxation = broad peak

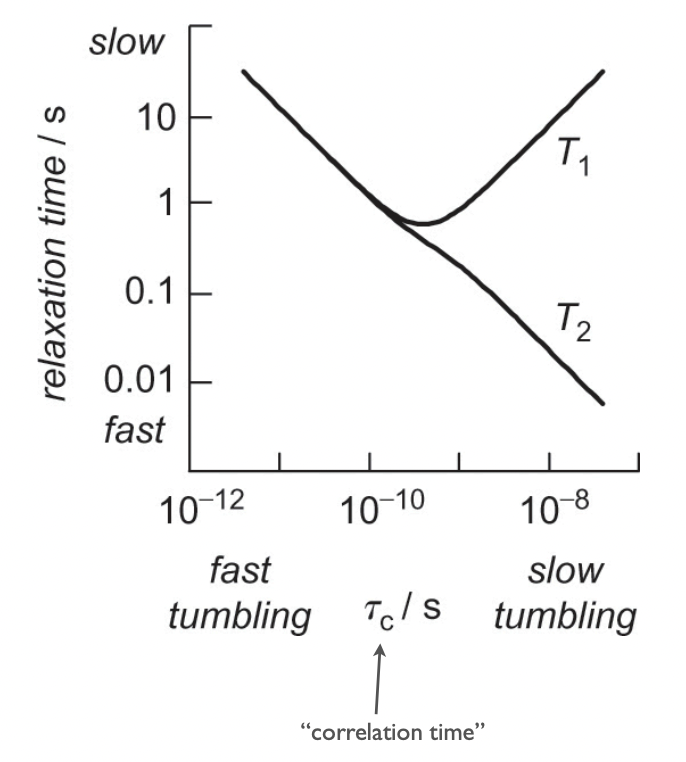
describe this graph

low τ(c) = fast molecular vibration = liquid

high  τ(c) = slow molecular vibration = solid

liquid = equal contribution of longitudinal/transverse relaxation

solid = transverse relaxation > longitudinal relaxation

T₂ relaxation in solids is much faster than T₁ because the local field fluctuations due to dipolar interactions cause rapid dephasing, but the lack of molecular motion limits the efficiency of energy transfer to the lattice (T₁).

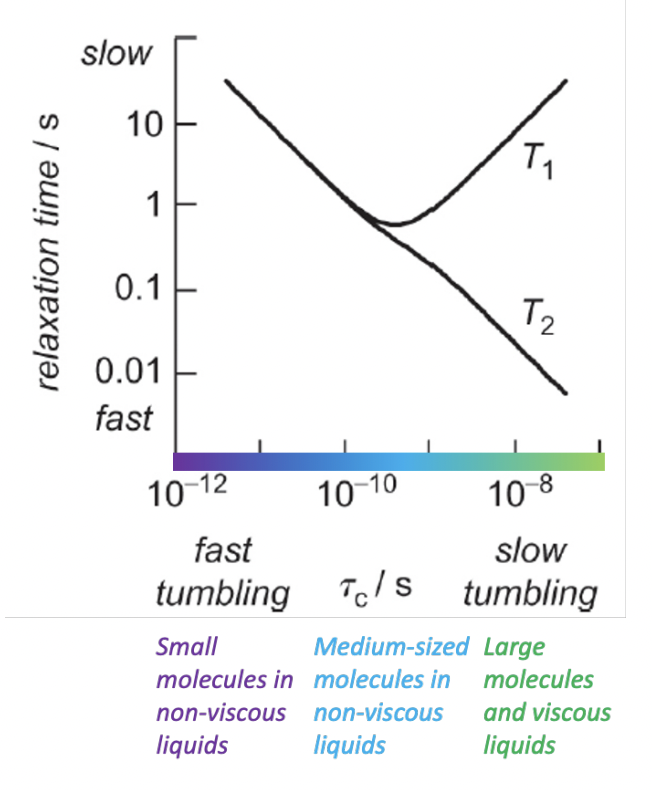
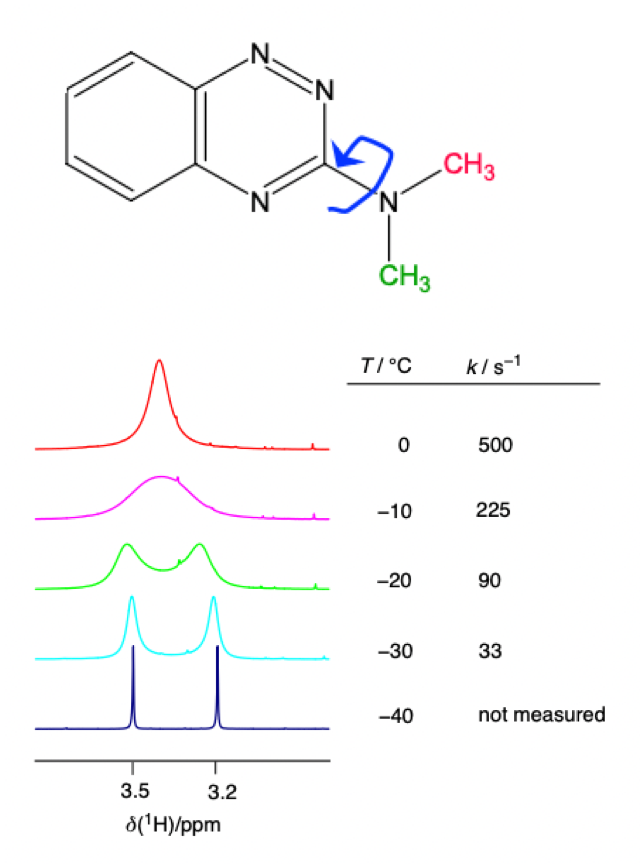
describe an application of NMR

= molecular dynamics

= can study inequivalent signals tending to equivalence due to molecular motion