Ap Calc Flashcards

sec (in terms of sine and/or cosine)

1/cos

cot (in terms of sine and/or cosine)

cos/sin

csc (in terms of sine and/or cosine)

1/sin

graph of sinx

graph of cos

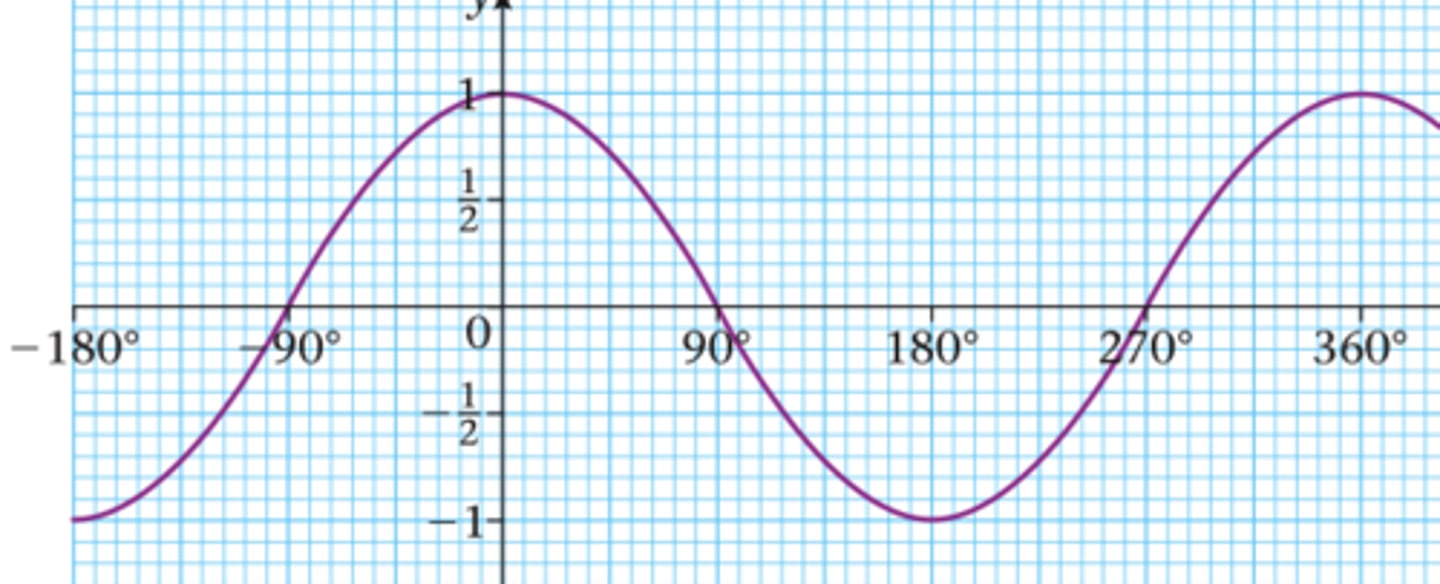
graph of tan

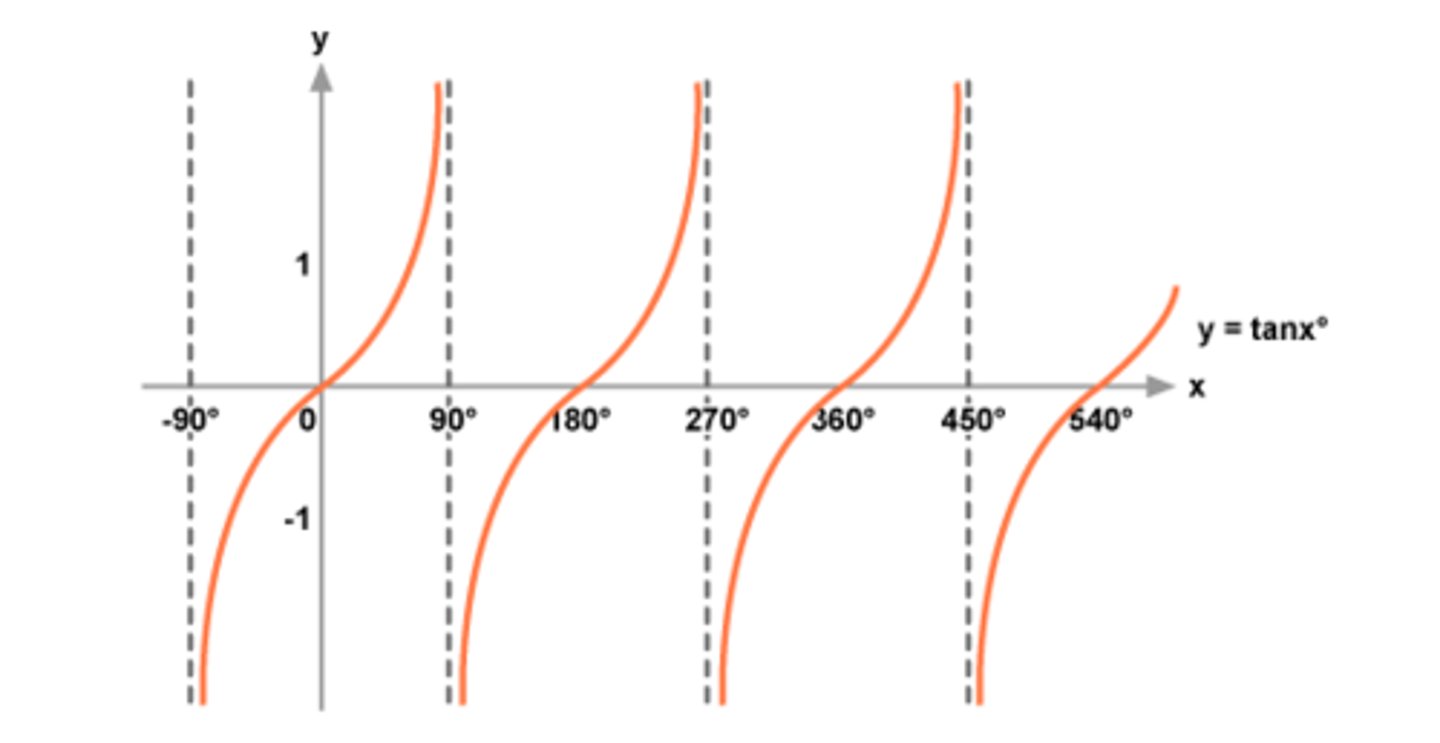
graph of sec x

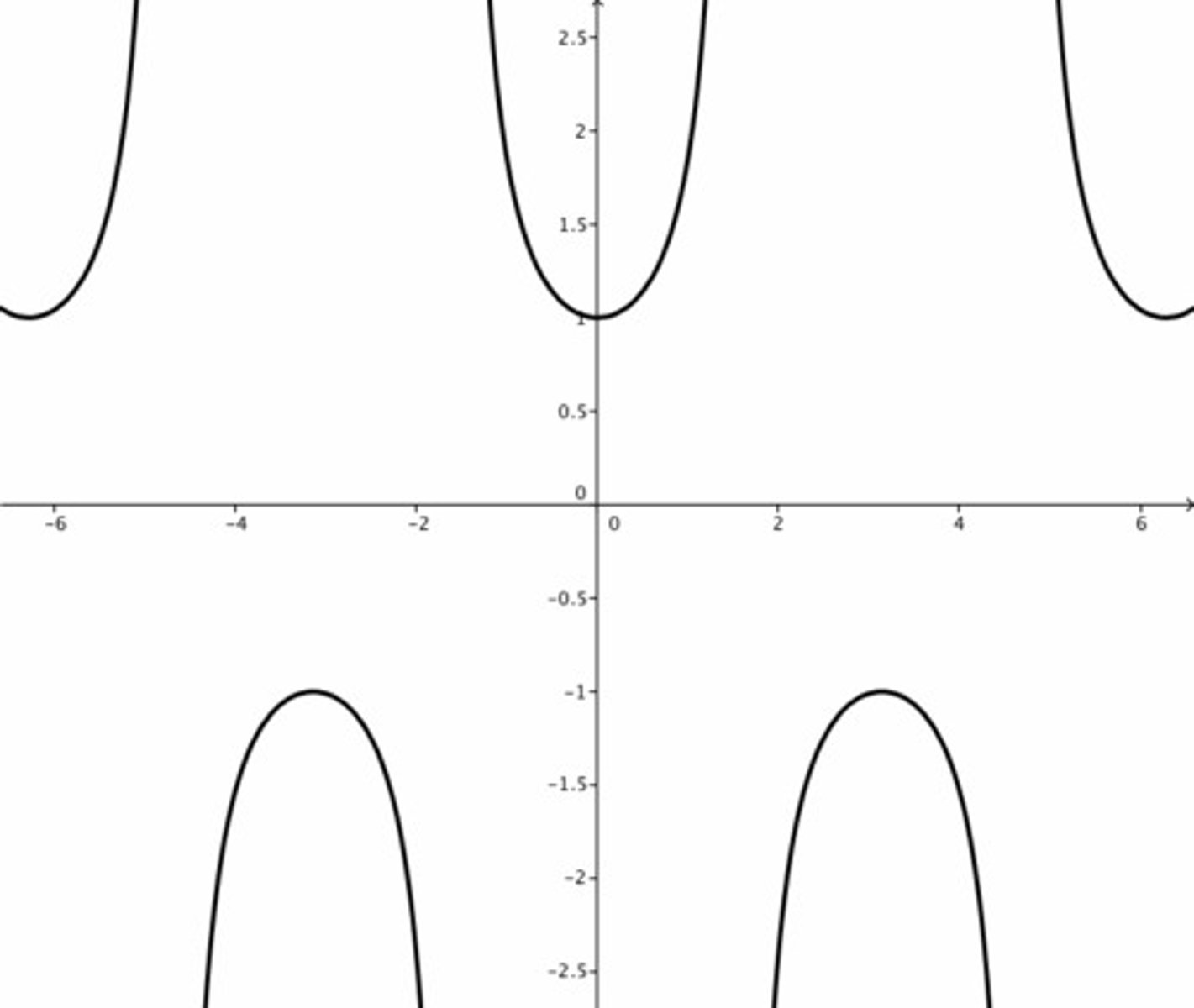
graph of lnx

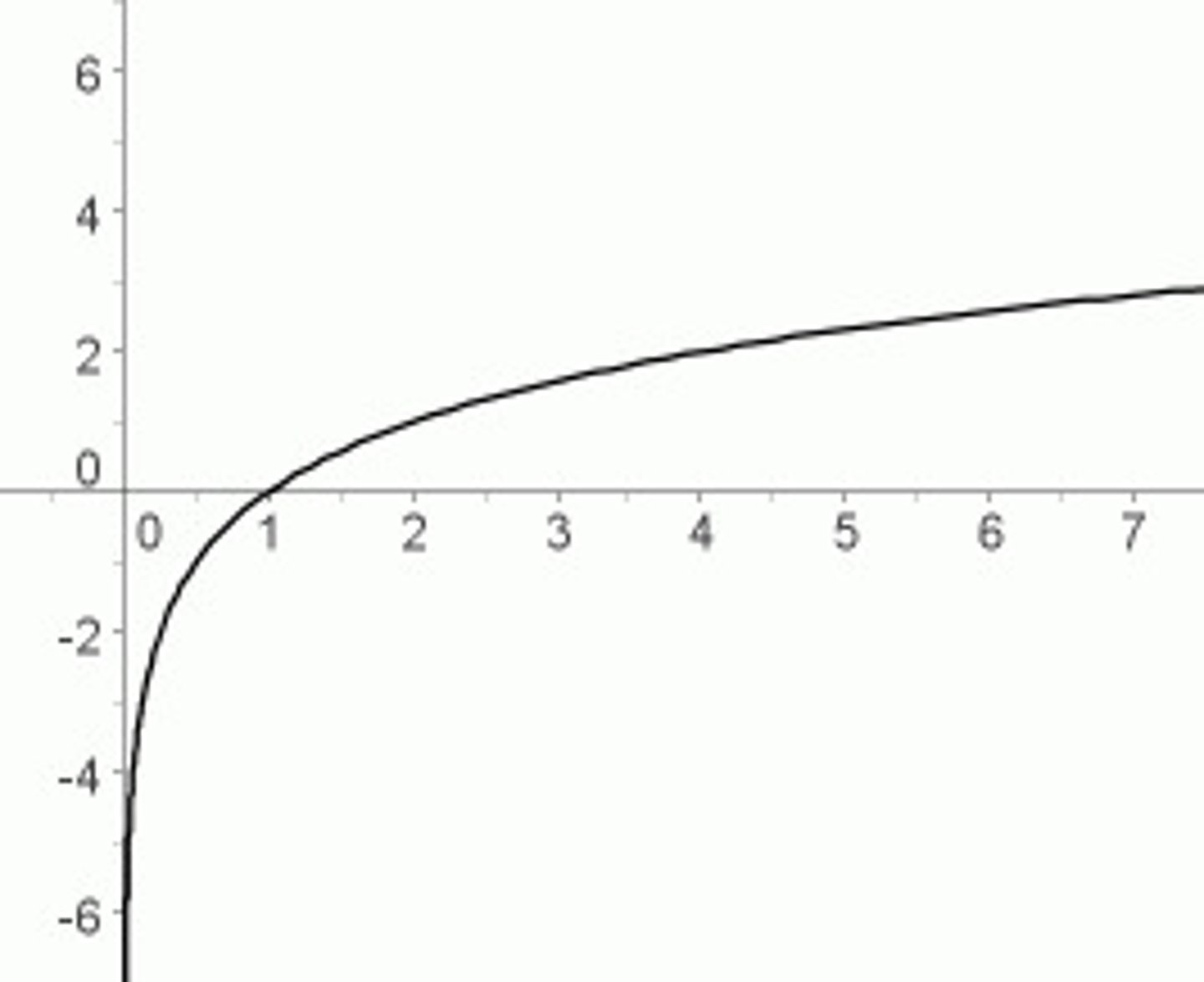
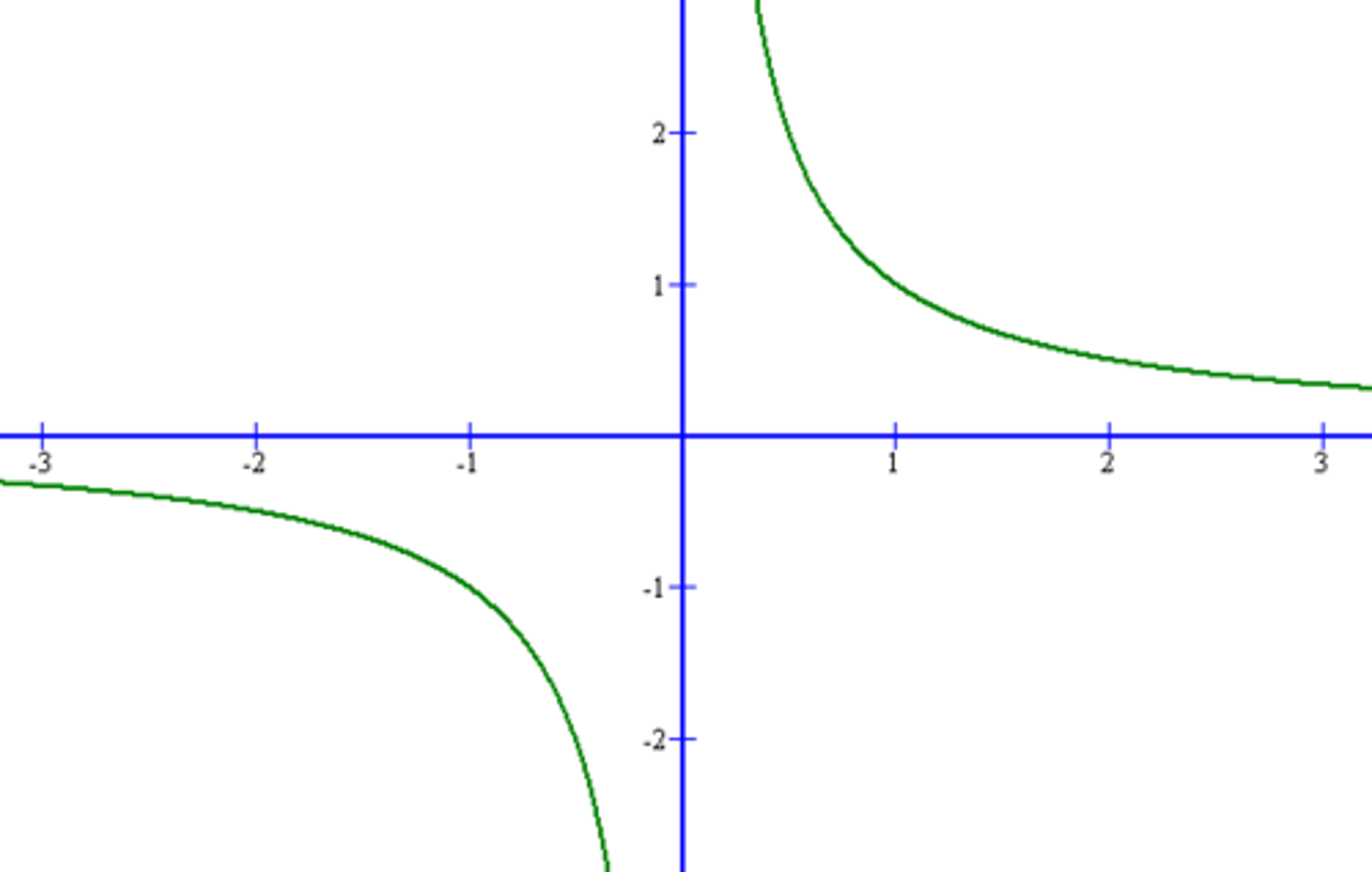
graph of 1/x

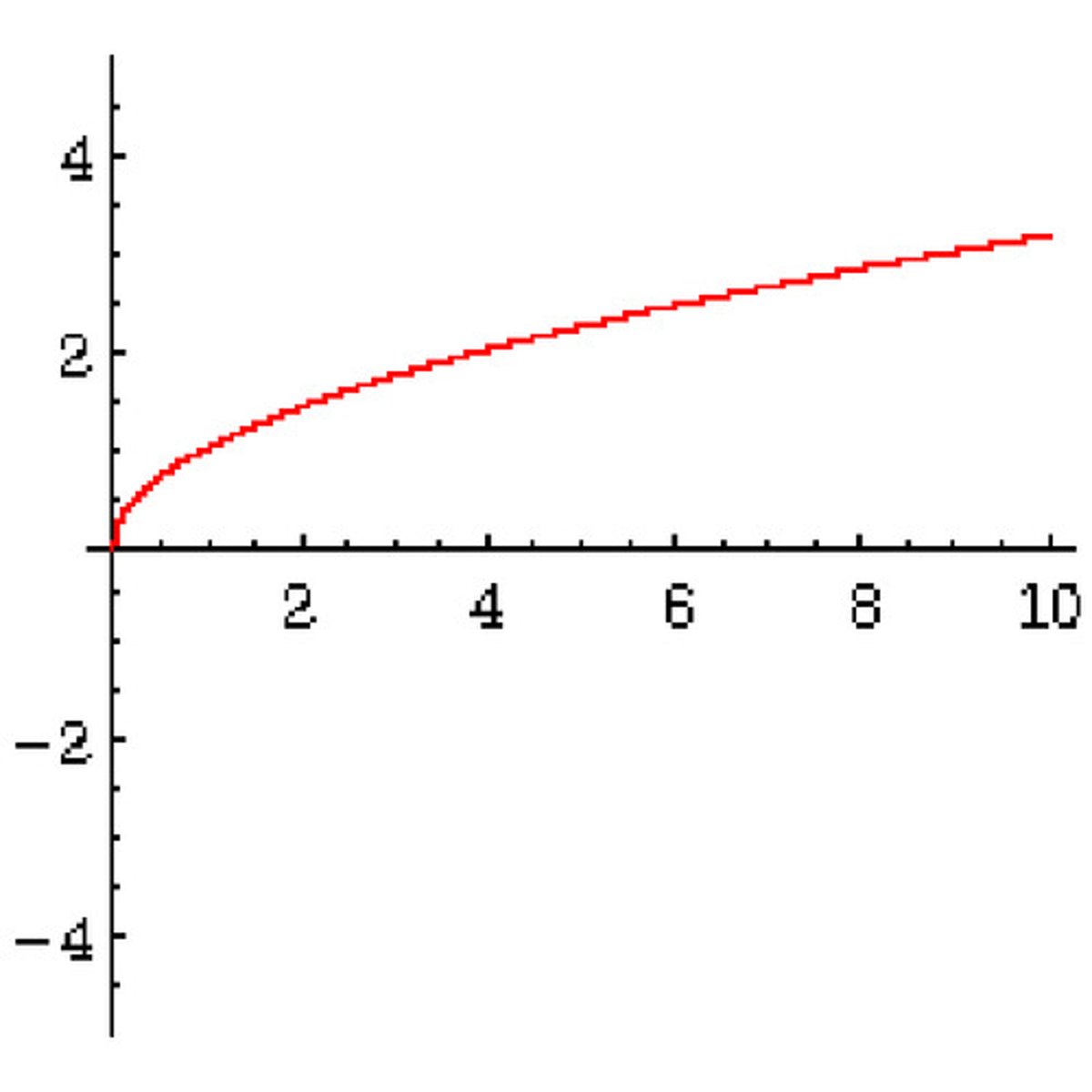
graph of sqrtx

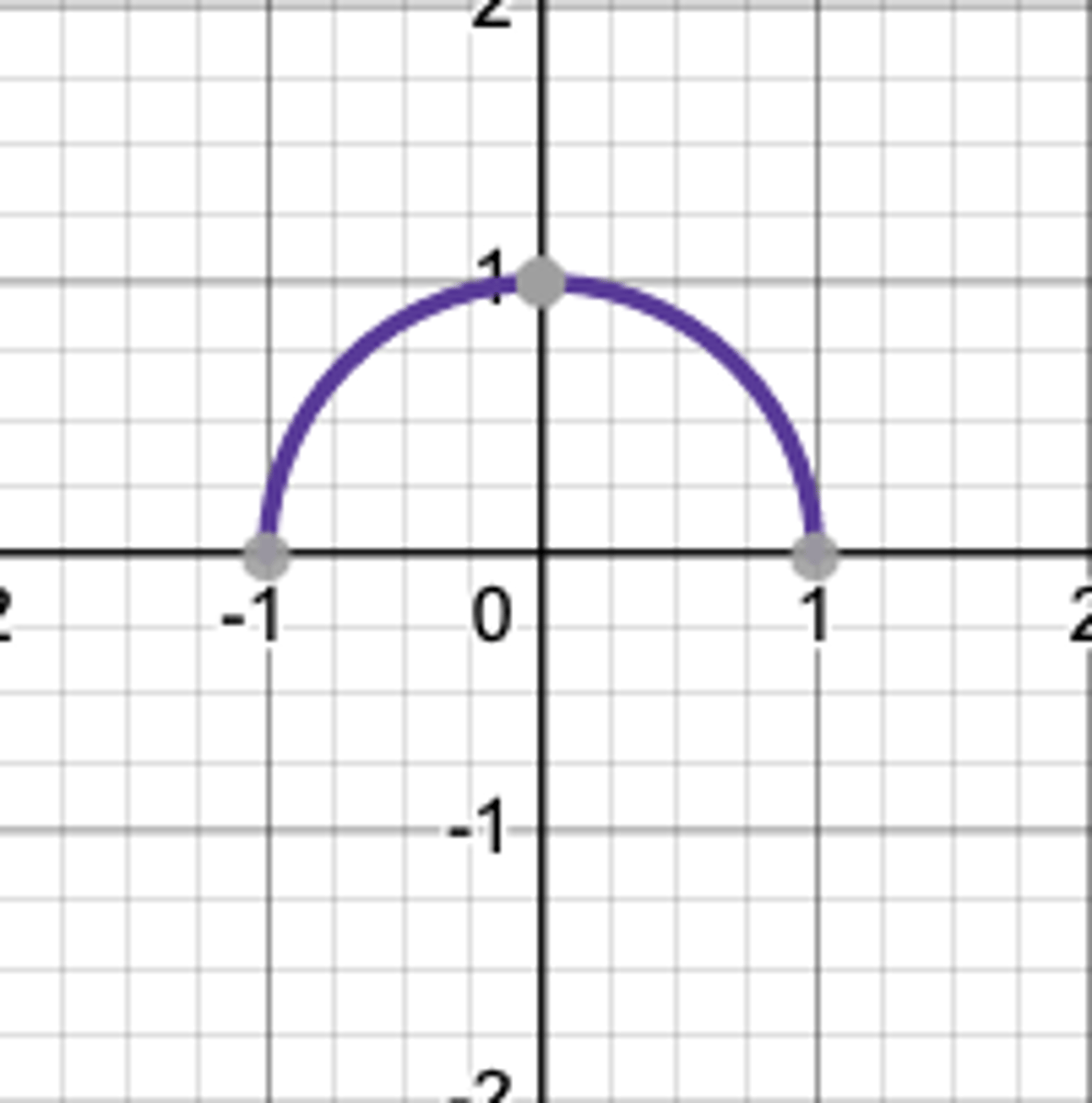
graph of sqrt 1-x^2

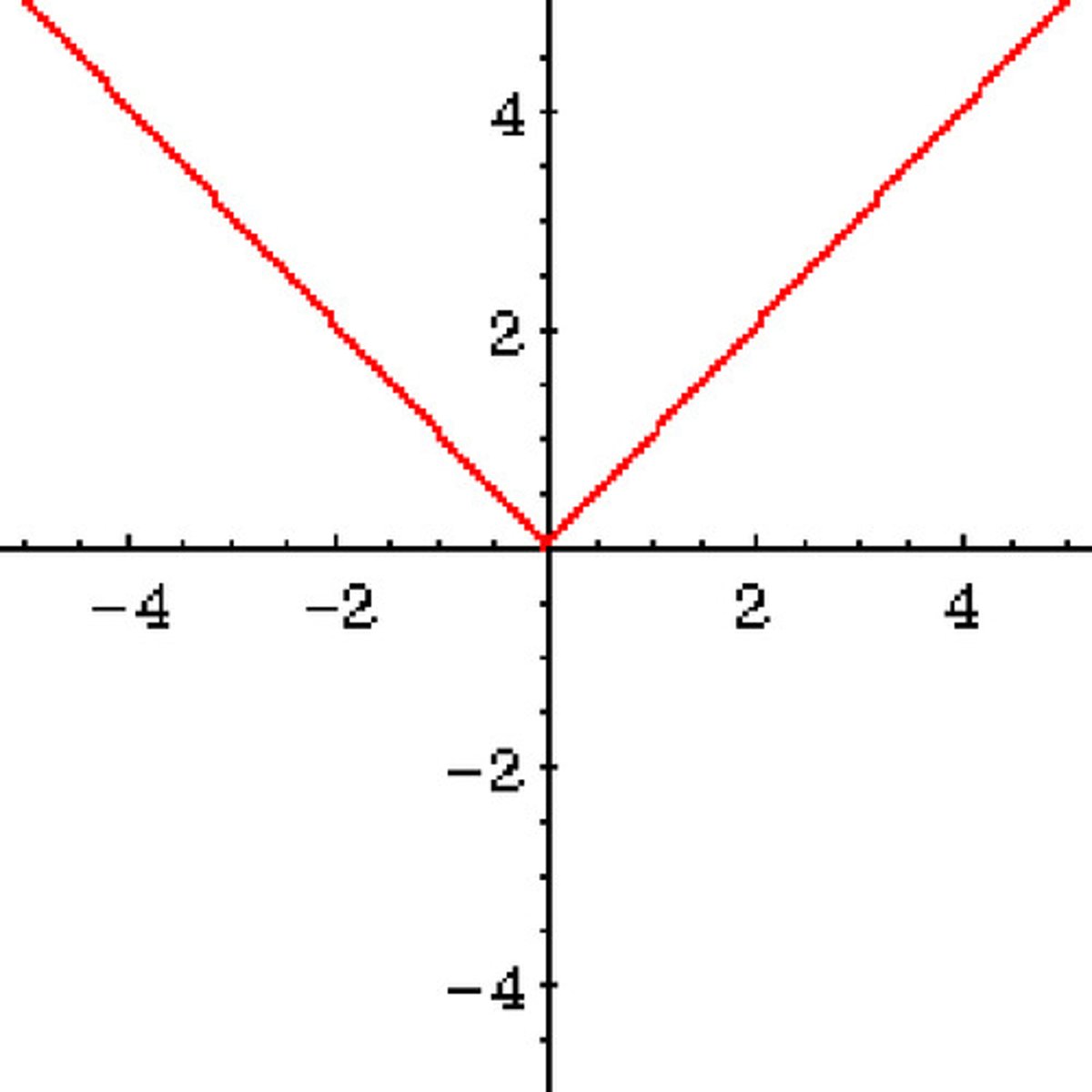
graph of abs value of x

Definition: a normal line is...

the line perpendicular to the tangent line at the point of tangency

Definition: an even function is...

Symmetric with respect to the y-axis. f(-x) = f(x)

Definition: an odd function is...

symmetric with respect to the origin. f(-x)= -f(x)

two formulas for the area of a triangle

A=1/2bh

A=1/2absinC

formula for the area of a circle

A=πr²

formula for the circumference of a circle

C = 2πr

formula for the volume of a cylinder

V=πr²h

formula for the volume of a cone

V=1/3πr²h

formula for the volume of a sphere

V=4/3πr^3

formula for the surface area of a sphere

4πr²

Definition: a tangent line is...

the line through a point on a curve with slope equal to the slope of the curve at that point

Definition: a secant line is...

Line connecting two points on a curve.

antiderivative of sinx

-cosx + c

antiderivative of cosx

sinx + c

antiderivative of sec^2x

tanx + C

antiderivative of csc^2x

-cotx + c

antiderivative of secxtanx

secx + c

antiderivative of cscxcotx

-cscx + C

trapezoidial rule for approximating f(x)dx

1/2h(y0 + 2y1 +2y2+...+2yn-1+yn)

average vale of f(x) on [a,b]

1/b-a (integral from a-b) f(x)dx

power rule for antiderivatives

(x^(n+1))/(n+1) + c, (n does not equal ^-1)

constant multiple rule for antidervatives

a constant coefficient can be brought to the outside

l'hopital's rule

If the limx→c (f(x)/g(x)) is indeterminate, then the limx→c (f(x)/g(x))=limx→c(f'(x)/g'(x)), if the new limit exists

mean value theorem for integration: if f(x) is continuous on [a,b], then...

...there exists a c e [a,b] duch that f(c) = 1/b-a (integral from a- b) f(x) dx

fundamental theorem of calculus (part 1) d/dx (integral from a - x) f(t) dt =

f(x)

fundamental theorem of calculus (part 2) (integral from a - b) f(x) dx =

F(b)-F(a), where F is an antiderivative of f

a differential equation is...

Equation involving one or more derivatives

to solve a differential equation...

first separate the variables (if needed) by multiplying or dividing, then integrate both sides

exponential growth and decay: if dy/dt = ky then...

y = Ce^kt, where C is the quantity at t = 0, and k is the constant of proportionality

(integral from a - b) (rate of change) dt

the amount which that quantity has changed from t = a to t = b

Definition: f(x) is continuous at x=c when...

1. f(c) exists;

2. the limit as x approaches c of f(x) exists; and

3. the limit as x approaches c of f(x) = f(c)

limit definition of derivative

f'(x) = lim change in x->0 f(x+∆ x) - f(x)∆x

alt limit definition of derivative

limit (as x approaches c)= f(x)-f(c)/x-c

What f'(x) tells you about a function

• slope of curve at a point

• slope of tangent line

• instantaneous rate of

change

definition: average rate of change

∆y/∆x = (f(b)-f(a))/(b-a)

Power rule for derivatives

(nu^n-1)u'

d/du(sinu)

(cosu)u'

d/du(cosu)

-(sinu)u'

d/du(tanu)

sec^2u

d/du(secu)

(secutanu)u'

d/du(cscu)

-cscucotu

d/du(cotu)

csc^2u

d/du(lnu)

u'/u

d/du(logau)

u'/ulna

d/du(a^u)

(lna)(a^u)(u')

Rolle's Theorem: If f is continuous on [a, b], differentiable on (a, b), and...

...f(a) = f(b), then there exists a c e (a,b) such that f'(c) = 0

Mean Value Theorem for Derivatives: If f is continuous on [a, b] and differentiable on (a, b), then...

there exists a value of c e (a,b) such that f'(c) = f(b)-f(a)/b-a

Extreme Value Theorem: If f is continuous on a closed interval, then...

...f must have both an absolute maximum and an absolute minimum on the interval

Intermediate Value Theorem: If f is continuous on [a, b], then...

...f must take on every y-value between f(a) and f(b)

If a function is differentiable at a point, then...

...it must be continuous at that point (differentiability implies continuity)

4 ways in which a function can fail to be differentiable at a point

discontinuity

corner

cusp

vertical line tangent

definition: a critical number (aka critical point or critical value) of f(x) is...

...a value of x in the domain of f at which either f'(x) = 0 or f'(x) does not exist

if f'(x) > 0, then...

f(x) is increasing

if f'(x) < 0, then...

f(x) is decreasing

if f'(x) = 0, then...

f(x) has a horizontal tangent

definition: f(x) is concave up when...

f'(x) is increasing

definition: f(x) is concave down when...

f'(x) is decreasing

f''(x) > 0

concave up

f''(x) < 0

concave down

a point of inflection is a point on the curve where...

concavity changes

To find a point of inflection

Look for where f'' changes signs, or, equivalently, where f' changes direction.

To find extreme values of a function, look for where...

f' is 0 or und (critical numbers)

at a max, the value of the derivative

f' changes from pos to neg (first deriv test)

at a min, the value of the derivative

f' changes from neg to pos(first deriv test)

second derivative test: if f' = 0 and...

f'' < 0, then f has a max; if f''>0 then f has a min